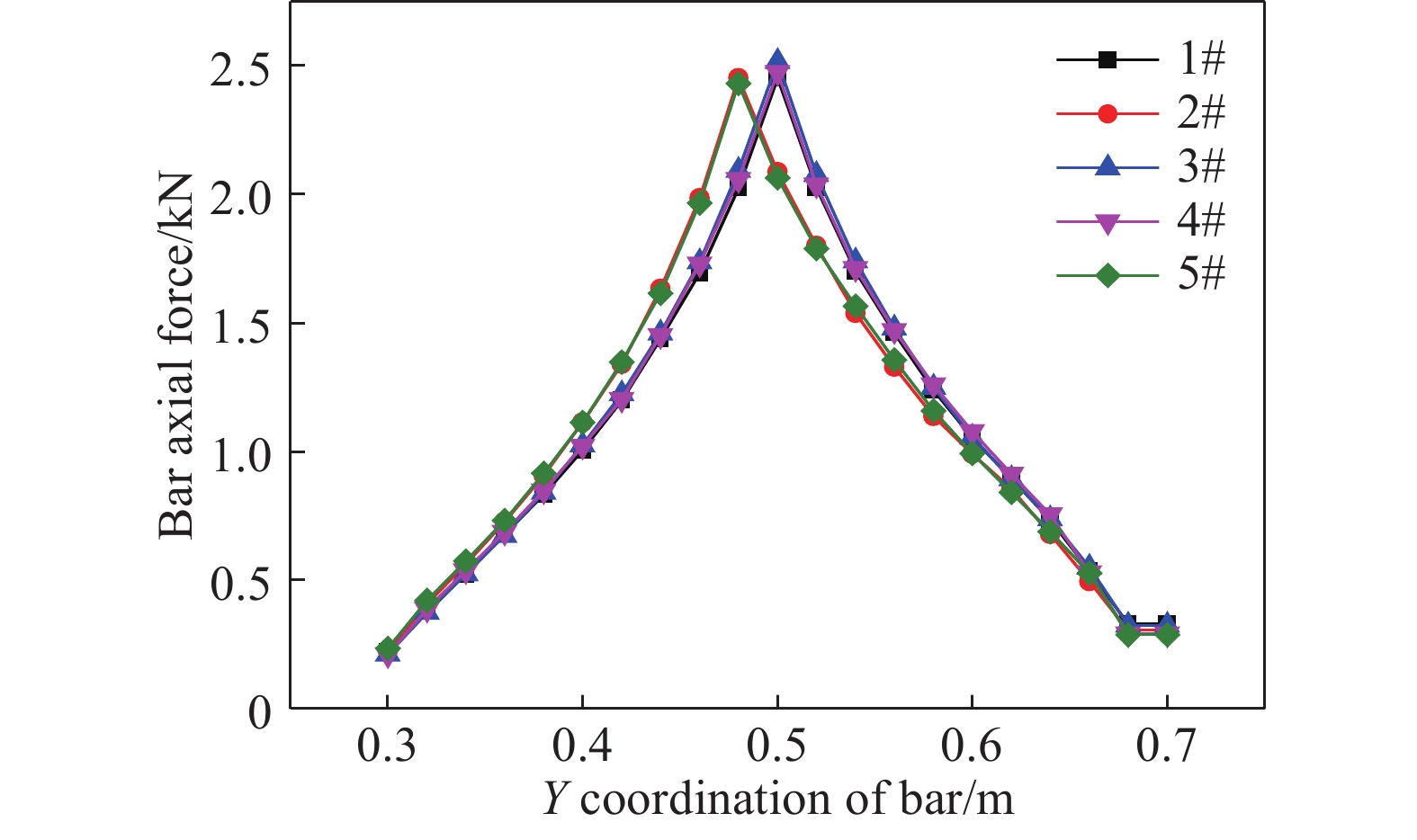
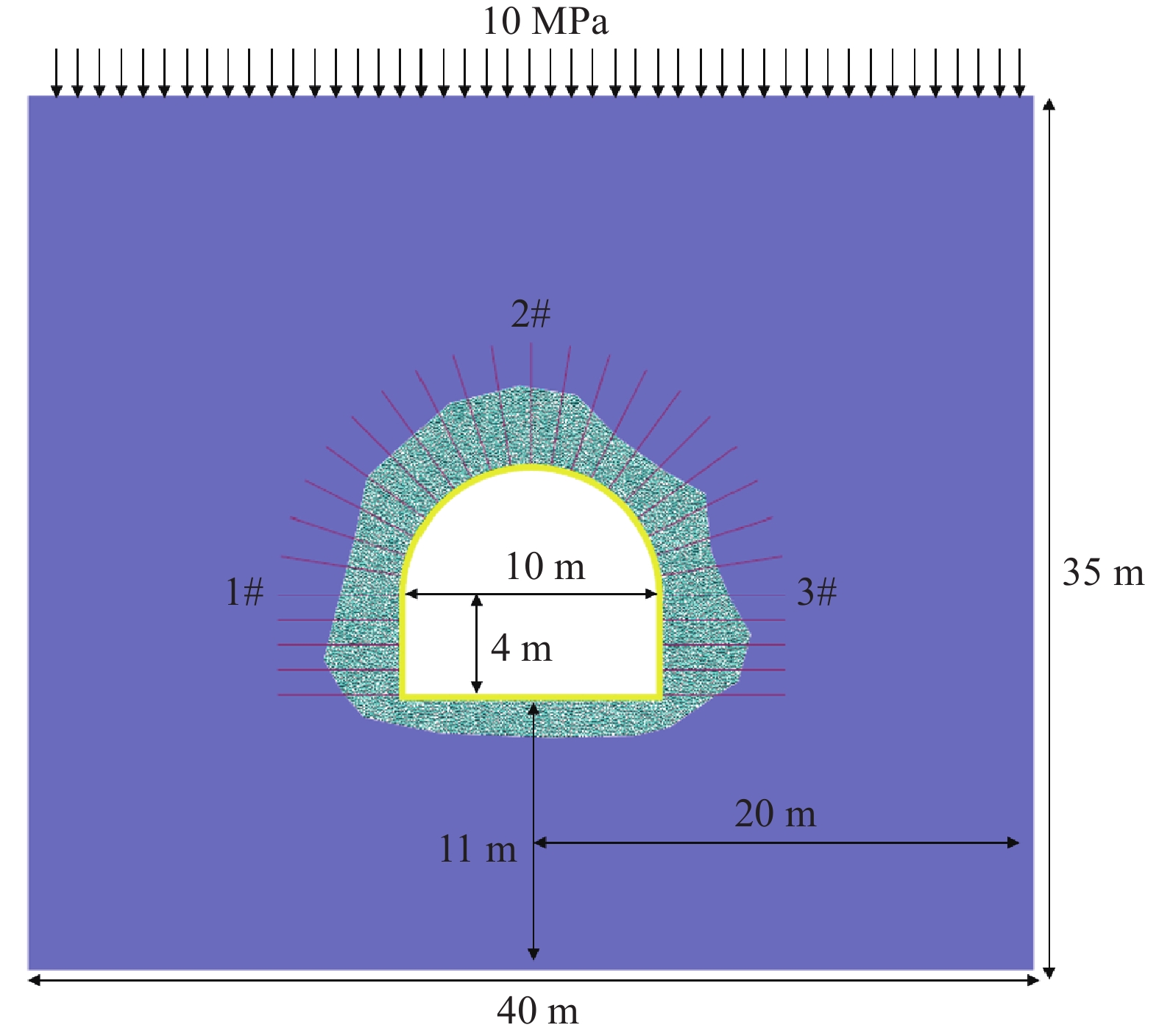
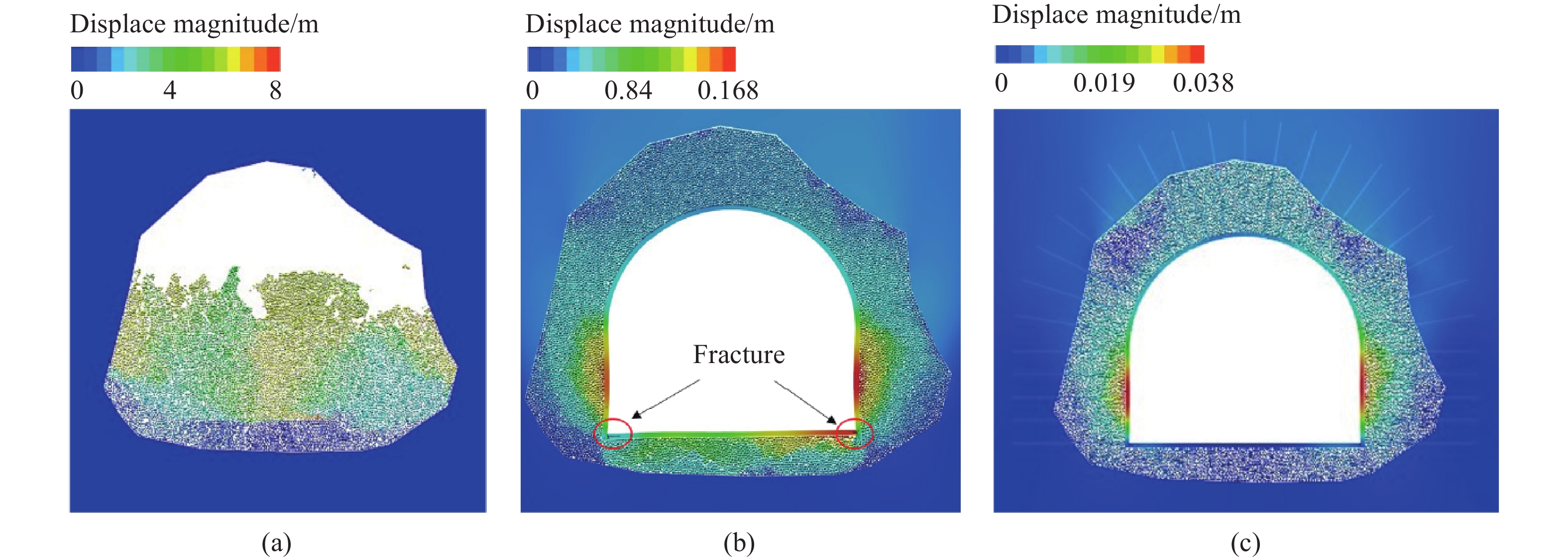
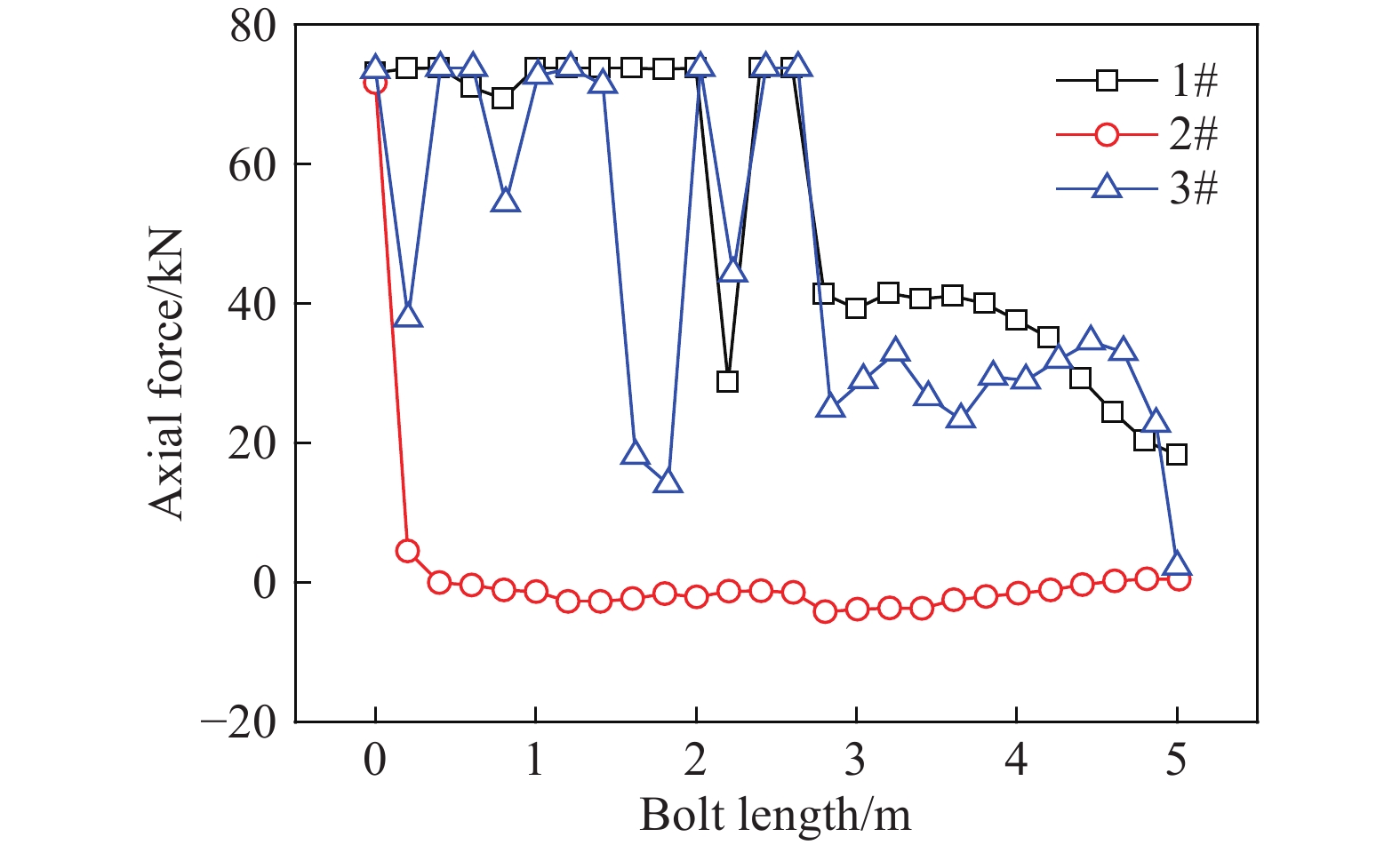
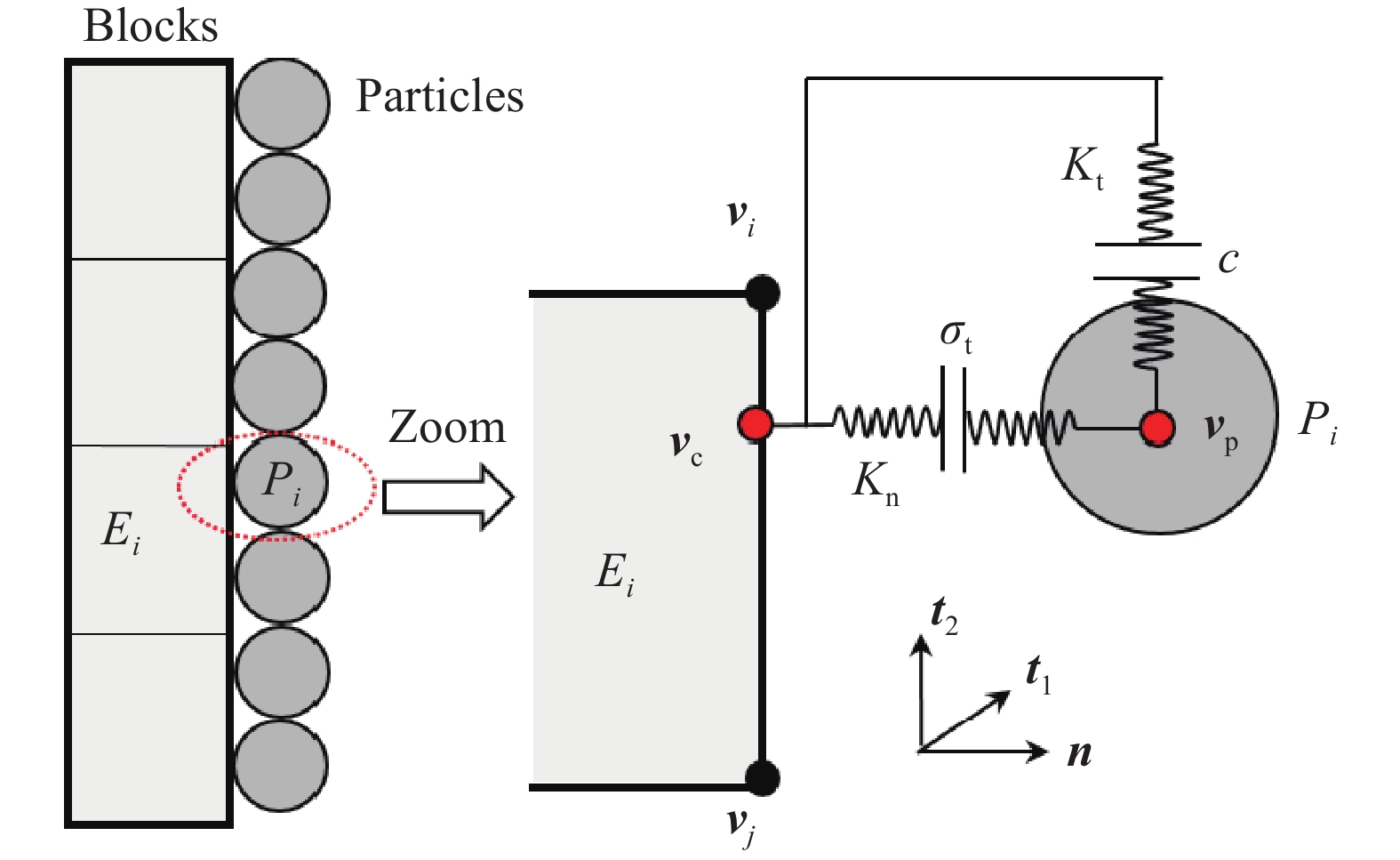
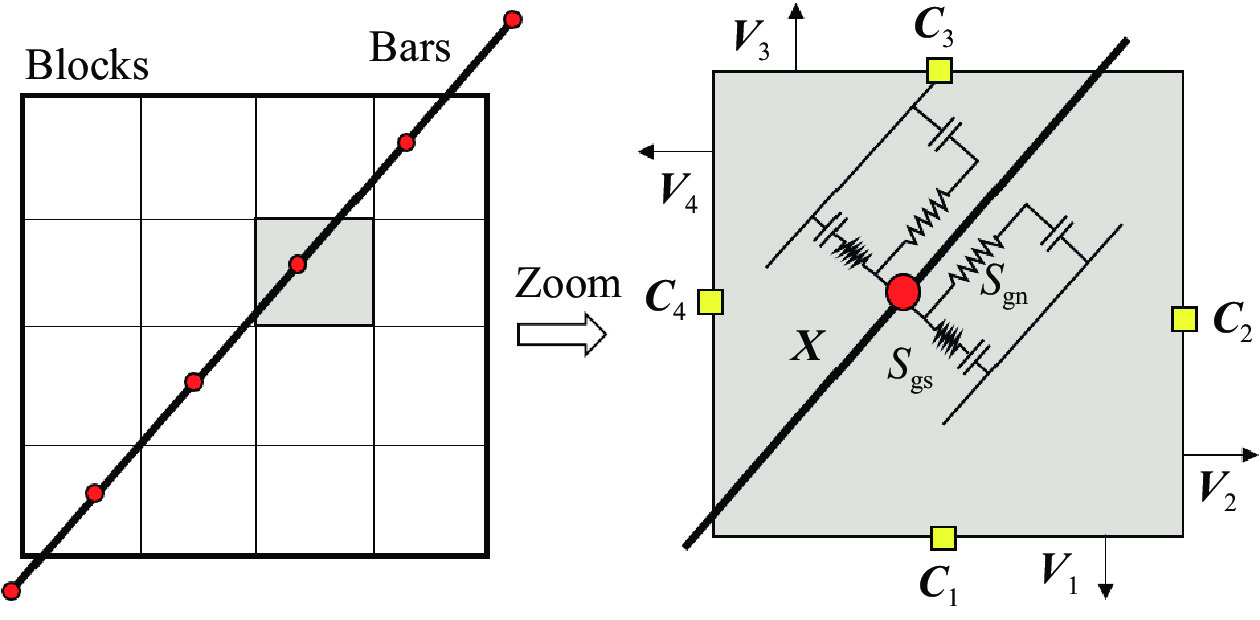
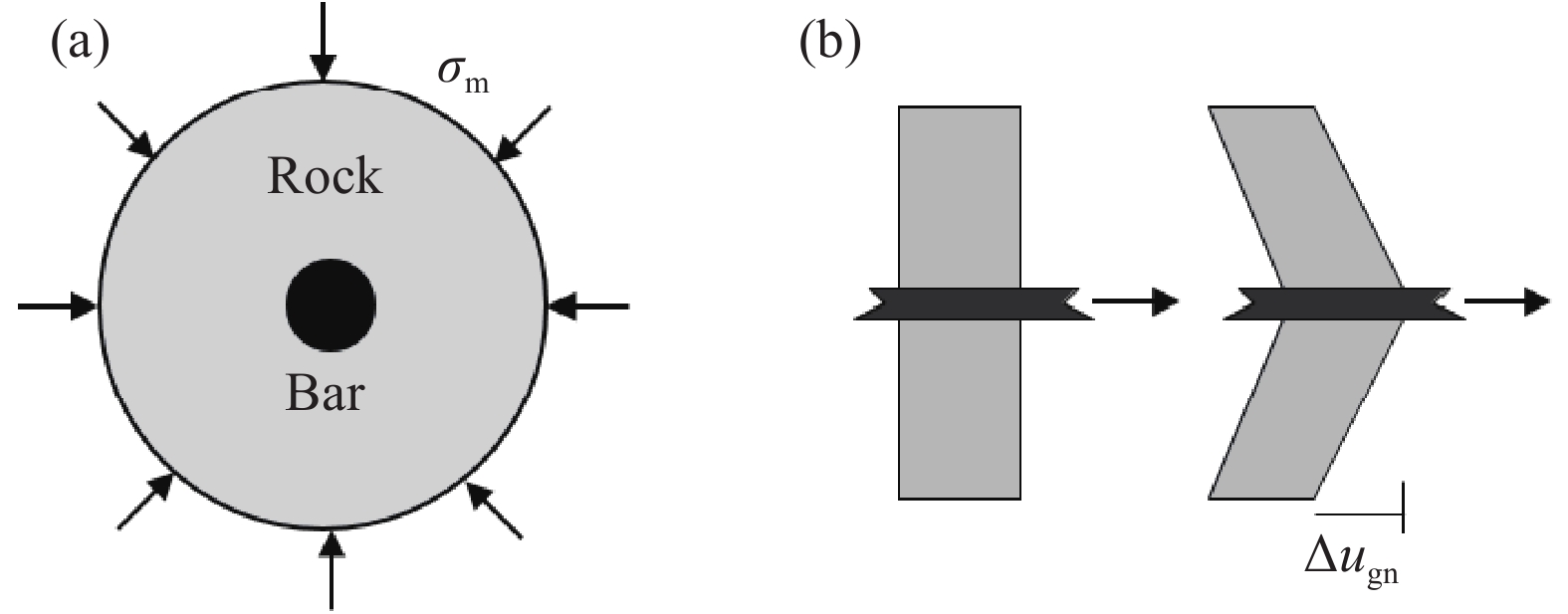
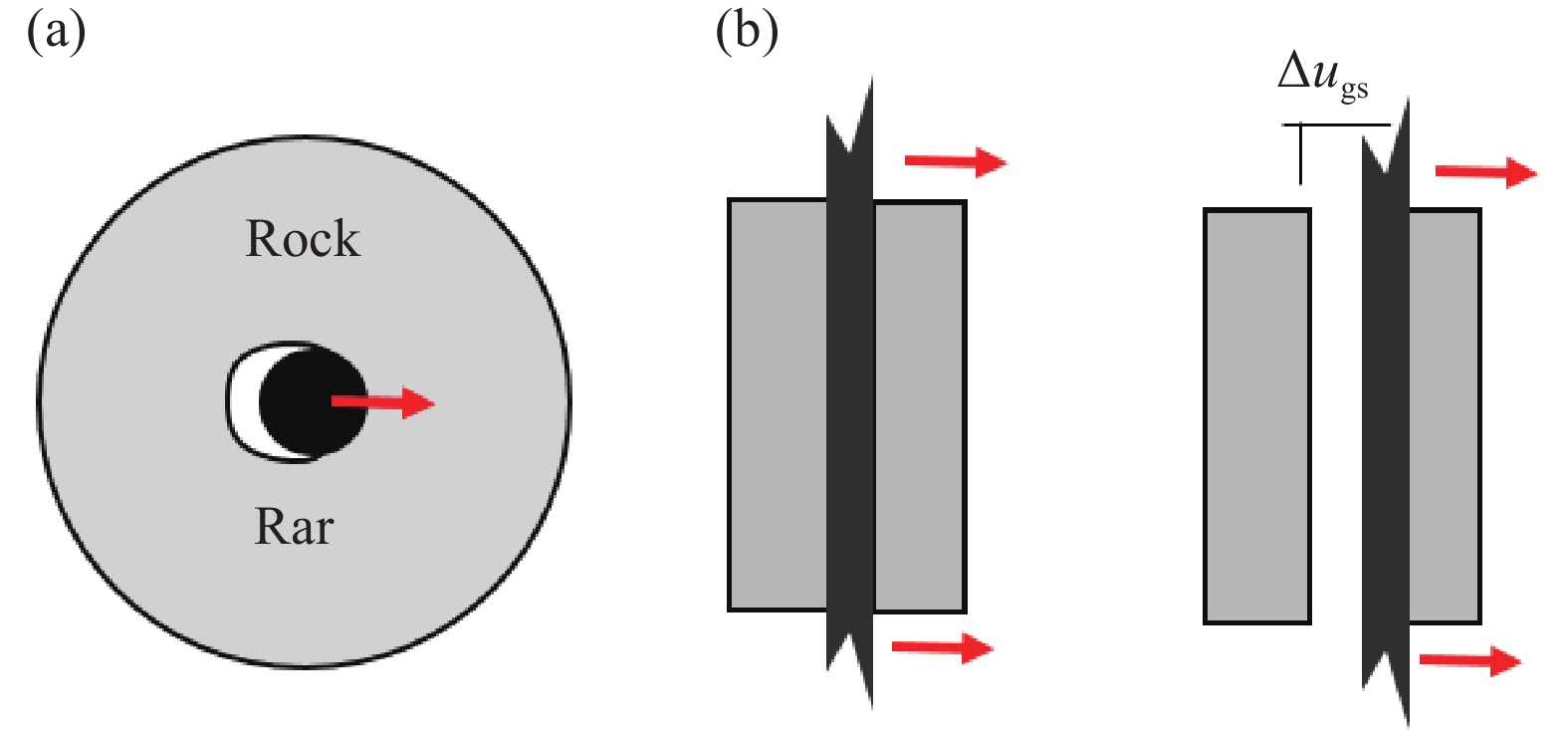
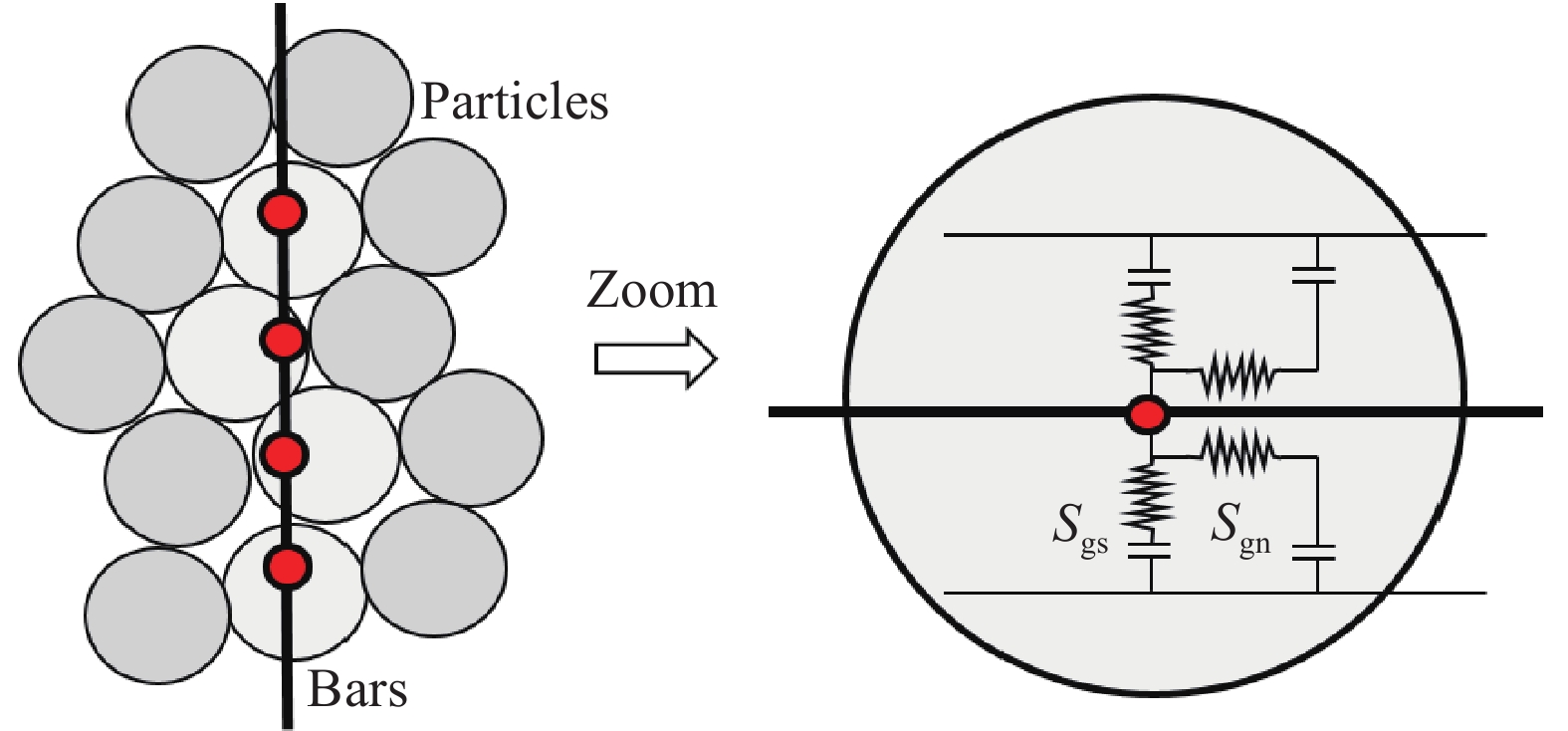
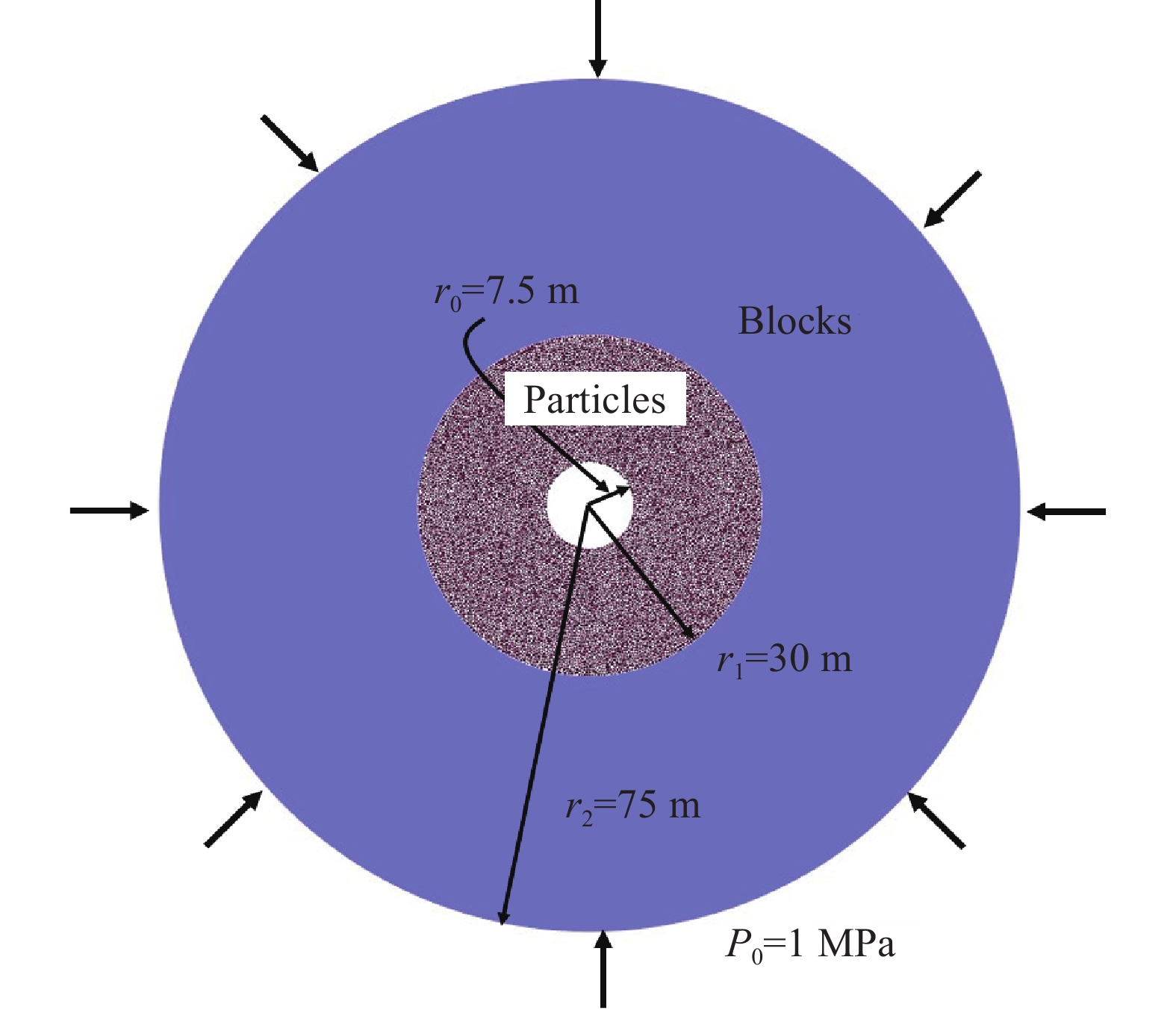
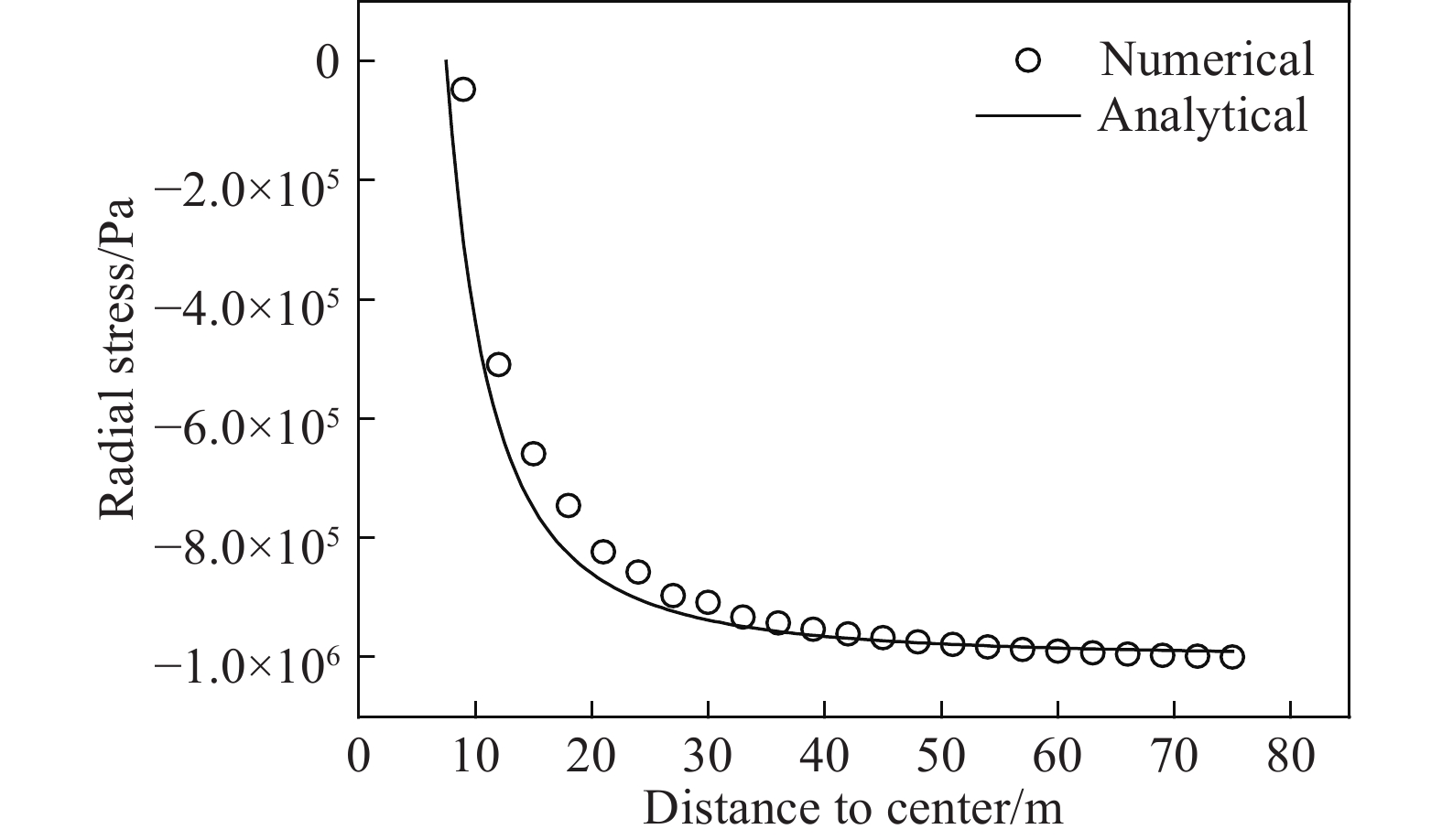
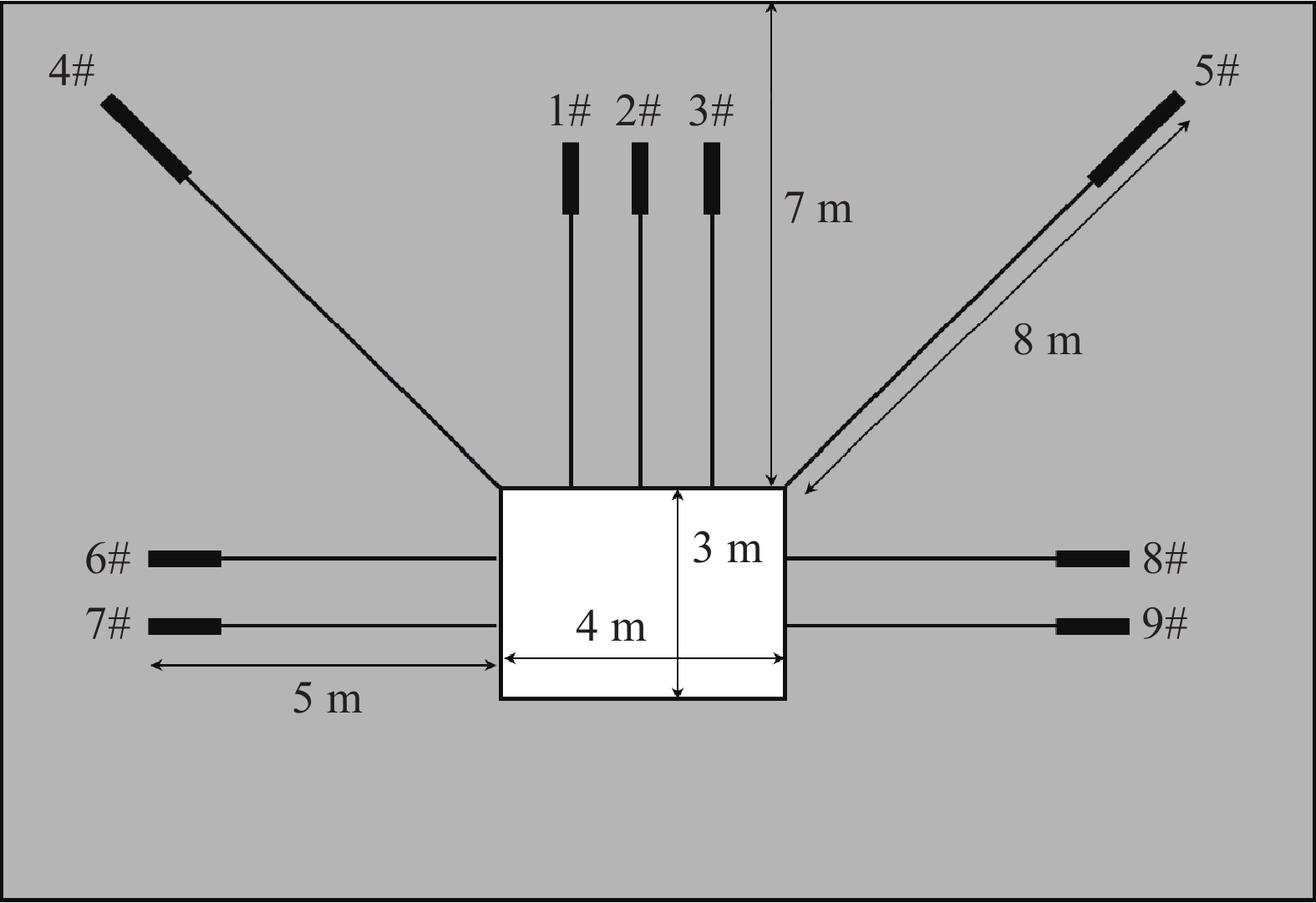
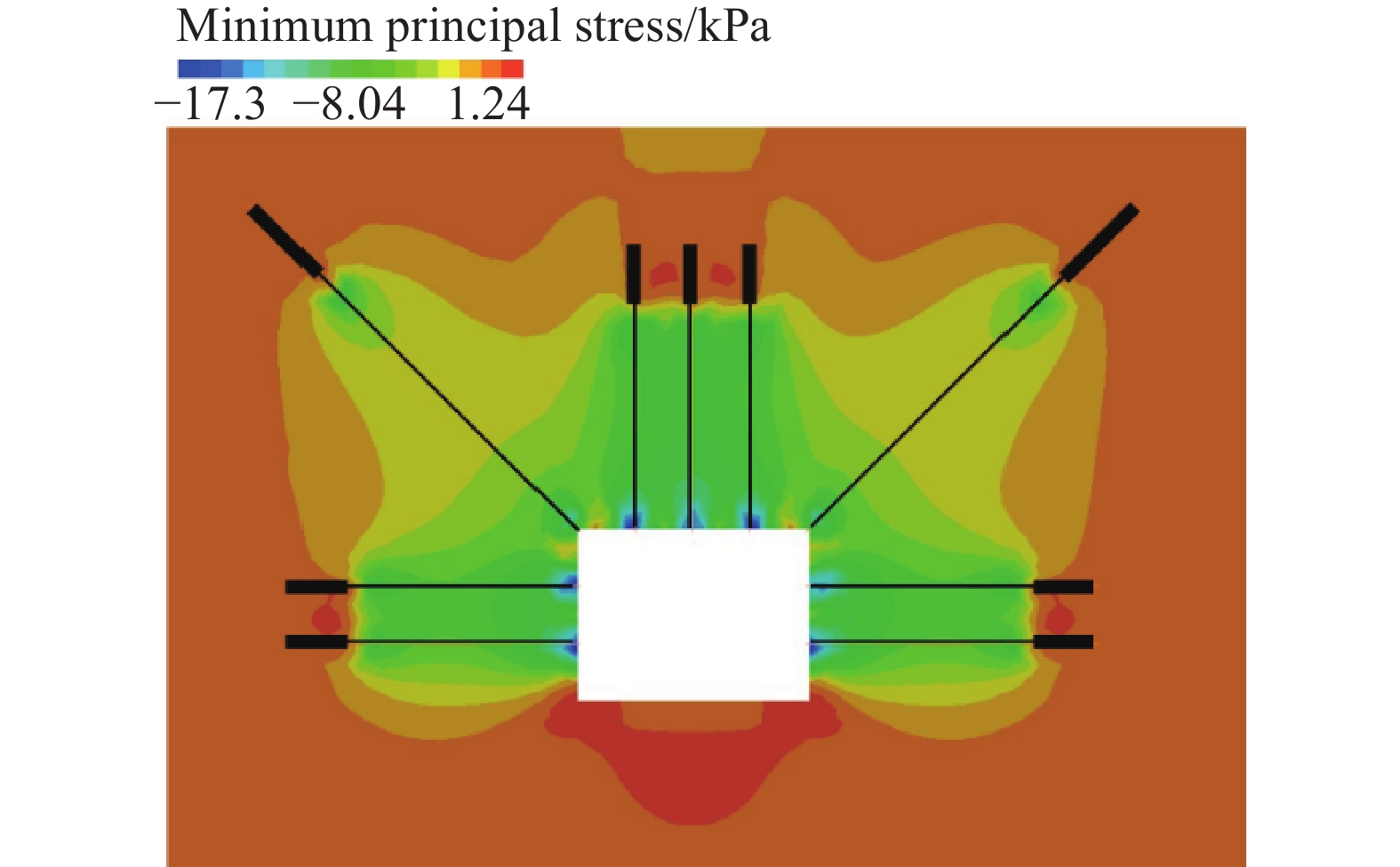
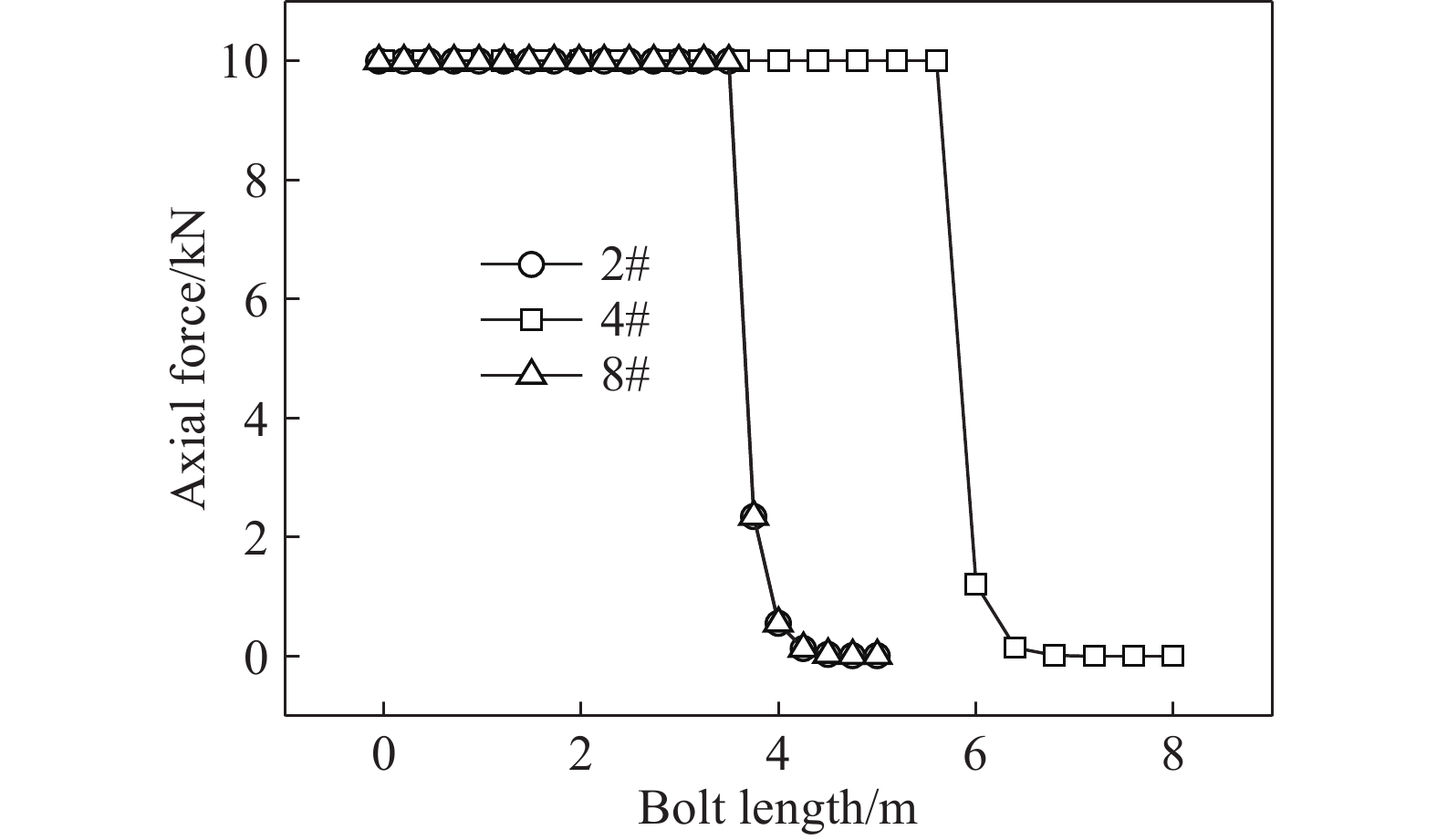
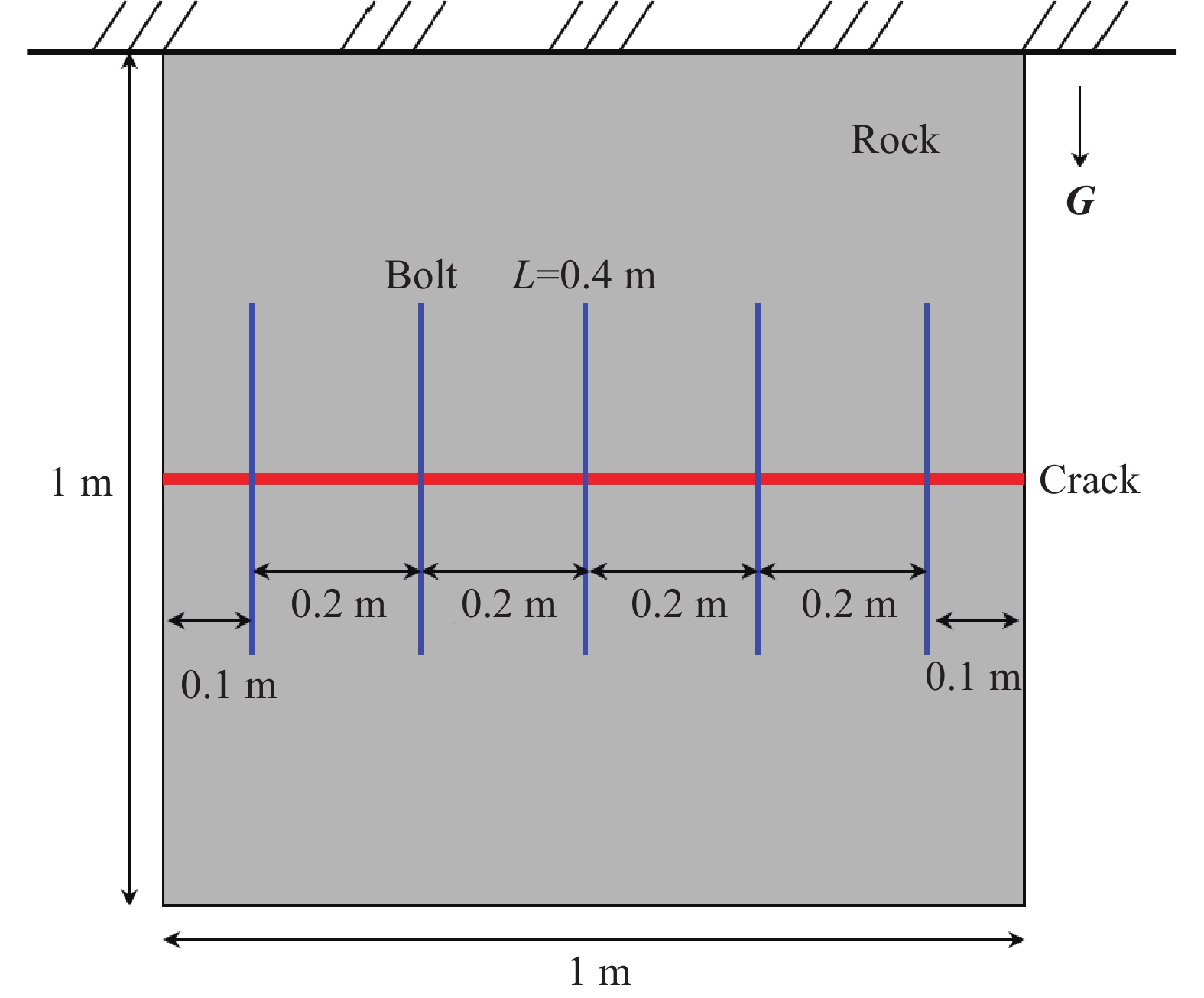
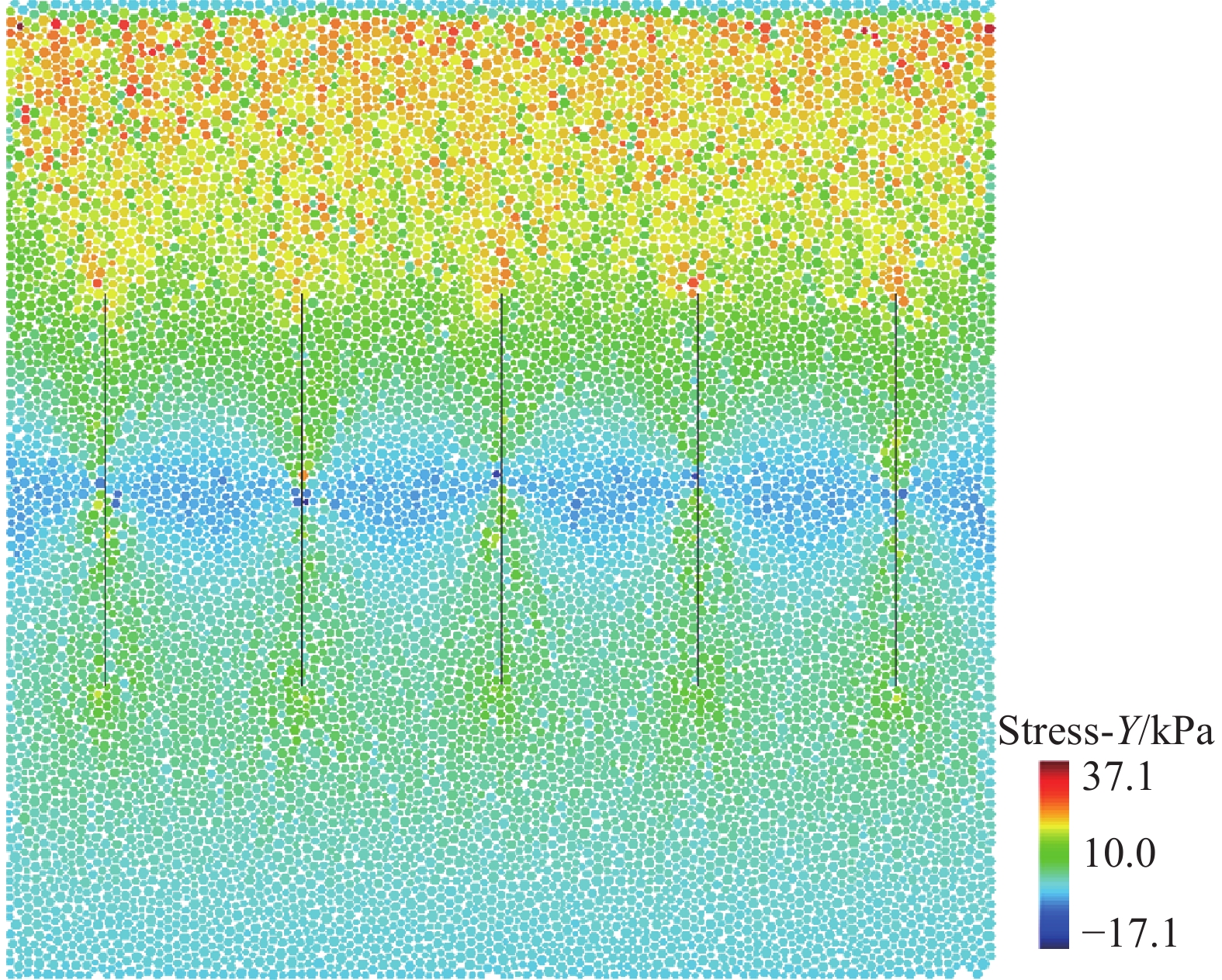
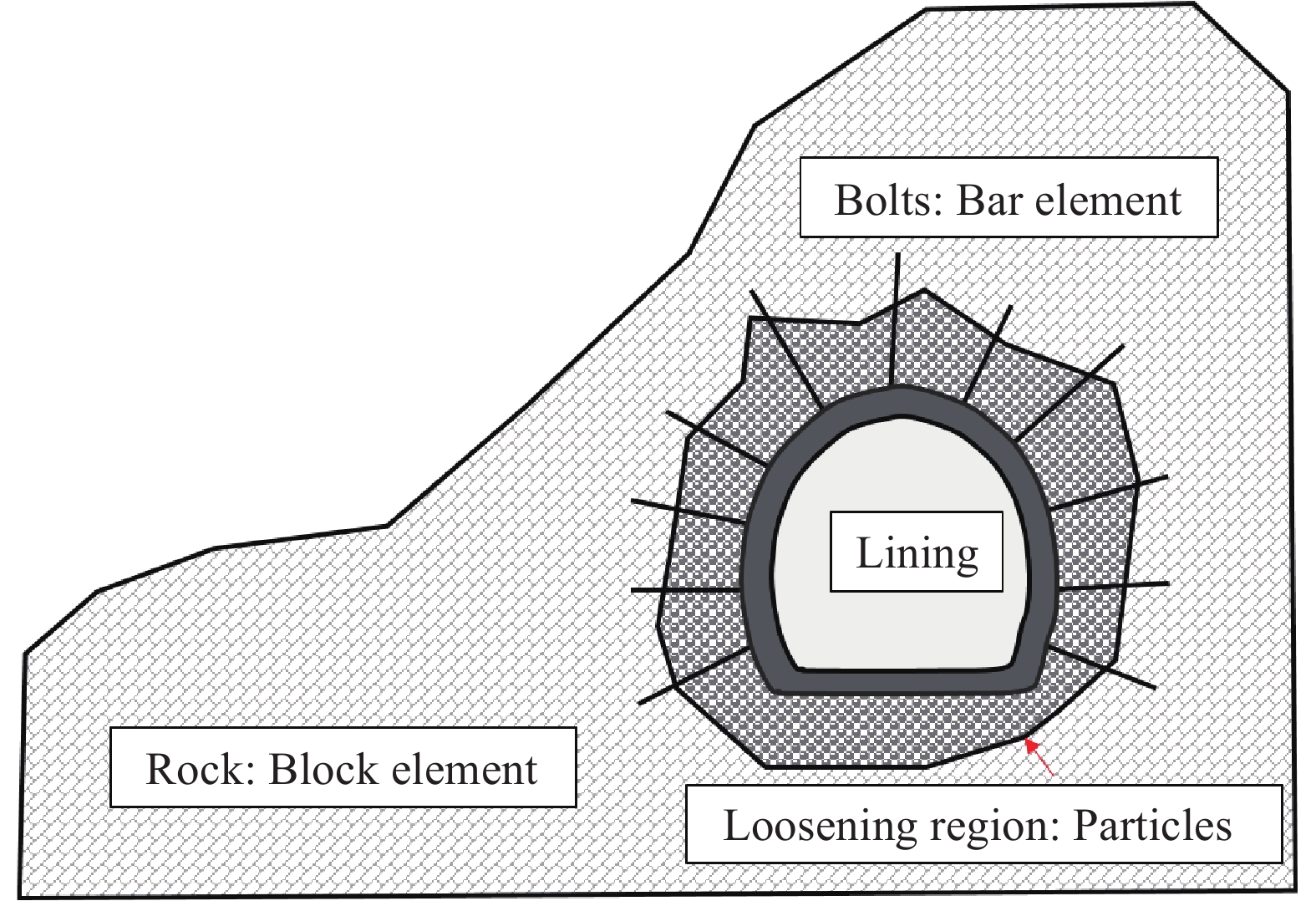
-
摘要: 為了模擬隧道開挖過程中邊幫的失穩垮塌過程以及錨桿對隧道的支護過程，提出了一種基于罰彈簧的塊體–顆粒–桿件的耦合方法。該耦合方法基于連續–非連續的數值模擬方法（CDEM），采用離散顆粒簇表征隧道周邊松動圈以內的破碎巖體，采用塊體單元表征松動圈以外的完整巖體，采用桿件單元描述錨桿及錨索等桿系類支護結構，采用插值耦合的方式實現桿件單元與離散顆粒及塊體單元間力與位移的傳遞，從而實現高應力環境下隧道開挖失穩過程的模擬及支護效果的評價。顆粒與塊體之間采用1根法向線性彈簧及2根切向線性彈簧進行耦合，法向彈簧引入拉伸斷裂本構，切向彈簧引入Mohr–Coulomb脆性斷裂本構。桿件與顆粒及桿件與塊體之間的耦合模式基本一致，包含1根沿著桿件軸向的罰彈簧Sgn及1根垂直于桿件軸向的罰彈簧Sgs，Sgn主要用于描述桿件與圍巖之間的拉拔效應及推壓效應，Sgs則主要用于描述桿件與圍巖之間的側向擠壓效應。圓形盾構隧道彈性場分析、預應力錨桿加固矩形巷道模擬、全長連接錨桿對巖塊的錨固作用分析、以及碎裂巖體中的隧道開挖支護效果分析等案例，證明了本文所述塊體–顆粒–桿件耦合算法的準確性及合理性。Abstract: During tunnel excavation, the stress of the surrounding rock is redistributed, leading to a local stress concentration around the tunnel. In addition, blasting excavation and other factors lead to a strength reduction of rock mass around the tunnel and eventually form a relaxation fracture zone (loosening zone). If supporting measures are not adopted in time during tunnel excavation, the rock strength in the loosening zone will be further reduced and eventually lead to overall instability and collapse. To simulate the bolt/cable supporting effect on the loosening zone and surrounding intact rock, a block–particle–bar coupling algorithm based on penalty springs is proposed. This coupling algorithm is based on the continuum–discontinuum element method (CDEM). CDEM is a dynamic, explicit solution algorithm based on a generalized Lagrange system. A strict controlling equation is established by the Lagrange energy system, and an explicit iterative solution of the dynamic relaxation method is used to realize a unified description of continuous and discontinuous media. The progressive failure of a solid is analyzed through the fracture of the bond between the blocks or particles. Using CDEM, the entire process of the solid from continuous deformation to fracture and movement can be simulated. In the block–particle–bar coupled algorithm, discrete particle clusters are adopted to represent the broken rock mass inside the loosening zone around the tunnel, block elements are used to represent the intact rock mass outside the loosening region, and bar elements are introduced to describe the supporting structures, such as bolts and cables. A contact coupling mode is adopted between particles and blocks, one normal spring and two tangential springs are constructed, and brittle Mohr–Coulomb fracture constitutive law and tensile fracture constitutive law are introduced to represent contact behavior. To realize the transmission of force and displacement, the interpolation coupling approach is adopted between the elements of bars and the elements of discrete particles or blocks. In this coupling mode, penalty springs Sgn and Sgs along and perpendicular to the axis of the bar, respectively, are established. Sgn and Sgs are mainly used to describe the pulling and pushing effect and the lateral compression effect between the bar and the surrounding rock, respectively. The coupling algorithm described in this paper is adopted to simulate the elastic field of a circular shield tunnel, rectangular tunnel reinforced by prestressed rock bolts, reinforcement of full-anchored rock bolts on surrounding rock, and the tunnel support effect in a jointed rock mass. The results of the four numerical cases show the accuracy and rationality of the coupling algorithm. Using this proposed algorithm, the progressive failure process of rock tunnels under high ground stress and the supporting process by lining and bolt (cable) can be accurately simulated.
-
Key words:
- finite element method /
- discrete element method /
- bolt /
- couple /
- tunnel /
- support
-
圖 4 桿件與圍巖之間的拉拔（推壓）失效示意. (a)軸向視圖；(b)側向視圖
Figure 4. Pull and push failure between the bar and surrounding rock: (a) axial view; (b) lateral view
圖 5 桿件與圍巖之間的側向擠壓失效示意. (a)軸向視圖；(b)側向視圖
Figure 5. Lateral compression failure between the bar and surrounding rock: (a) axial view; (b) lateral view
圖 9 矩形巷道預應力錨桿支護數值模型
Figure 9. Numerical model of a rectangular tunnel reinforced by prestressed rock bolts
圖 13 錨桿加固后巖塊上的豎向應力云圖
Figure 13. Vertical stress contour of the rock reinforced by full-anchored bolts
圖 16 三種模擬工況下隧道的總位移云圖. (a)工況A; (b)工況B; (c)工況C
Figure 16. Displacement magnitude contour of the tunnel under three numerical cases: (a) case A; (b) case B; (c) case C
表 1 力學參數
Table 1. Mechanical parameters
Materials Density/(kg·m–3) Elasticity
modulus/
GPaPoisson’s
ratioCohesion/MPa Tensile
strength/MPaInternal friction
angle/(°)Dilation angle/(°) Surrounding rock 2200 10 0.3 3 3 25 10 Broken zone 2200 5 0.33 1 1 20 10 Lining structure 2500 36 0.25 8 4 35 15 
下載: 導出CSV
www.77susu.com<span id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> <span id="fpn9h"><noframes id="fpn9h"> <th id="fpn9h"></th> <strike id="fpn9h"><noframes id="fpn9h"><strike id="fpn9h"></strike> <th id="fpn9h"><noframes id="fpn9h"> <span id="fpn9h"><video id="fpn9h"></video></span> <ruby id="fpn9h"></ruby> <strike id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> -
參考文獻
[1] Rahaman O, Kumar J. Stability analysis of twin horse-shoe shaped tunnels in rock mass. Tunn Undergr Space Technol, 2020, 98: 103354 doi: 10.1016/j.tust.2020.103354 [2] Wu G J, Chen W Z, Rong C, et al. Elastoplastic damage evolution constitutive model of saturated rock with respect to volumetric strain in rock and its engineering application. Tunn Undergr Space Technol, 2020, 97: 103284 doi: 10.1016/j.tust.2020.103284 [3] Wasilewski S. Gas-dynamic phenomena caused by rock mass tremors and rock bursts. Int J Min Sci Technol, 2020, 30(3): 413 doi: 10.1016/j.ijmst.2020.03.012 [4] He M C, Li J Y, Ren F Q. Rock burst criterion based on clay mineral content. Arab J Geosci, 2020, 13(4): 185 doi: 10.1007/s12517-020-5199-x [5] Yang Z Q, Liu C, Zhu H Z, et al. Mechanism of rock burst caused by fracture of key strata during irregular working face mining and its prevention methods. Int J Min Sci Technol, 2019, 29(6): 889 doi: 10.1016/j.ijmst.2018.07.005 [6] Chen W T, Huan Y, Fan P X. Numerical analysis on minimal safe distance between two opposite excavation faces of deep-buried tunnel. Appl Mech Mater, 2013, 353-356: 1315 doi: 10.4028/www.scientific.net/AMM.353-356.1315 [7] Liu J, Liu X, Ren L. Research and discuss on development of deep tunnel bolt supporting technology. Appl Mech Mater, 2012, 204-208: 1542 doi: 10.4028/www.scientific.net/AMM.204-208.1542 [8] Sun S R, Yue L, Wu J M, et al. Case study on influence of step blast-excavation on support systems of existing service tunnel with small interval. Adv Mech Eng, 2013, 5: 257457 doi: 10.1155/2013/257457 [9] Liu K, Chen S L, Gu X Q. Analytical and numerical analyses of tunnel excavation problem using an extended drucker-prager model. Rock Mech Rock Eng, 2020, 53(4): 1777 doi: 10.1007/s00603-019-01992-5 [10] Li W T, Yang N, Yang B, et al. An improved numerical simulation approach for arch-bolt supported tunnels with large deformation. Tunn Undergr Space Technol, 2018, 77: 1 doi: 10.1016/j.tust.2018.03.001 [11] Wang F Y, Qian D L. Difference solution for a circular tunnel excavated in strain-softening rock mass considering decayed confinement. Tunn Undergr Space Technol, 2018, 82: 66 doi: 10.1016/j.tust.2018.08.001 [12] Wu L, Zhang X D, Zhang Z H, et al. 3D discrete element method modelling of tunnel construction impact on an adjacent tunnel. KSCE J Civ Eng, 2020, 24(2): 657 doi: 10.1007/s12205-020-2054-2 [13] Boon C W, Houlsby G T, Utili S. Designing tunnel support in jointed rock masses via the DEM. Rock Mech Rock Eng, 2015, 48(2): 603 doi: 10.1007/s00603-014-0579-8 [14] Wang X, Cai M. A DFN-DEM multi-scale modeling approach for simulating tunnel excavation response in jointed rock masses. Rock Mech Rock Eng, 2020, 53(3): 1053 doi: 10.1007/s00603-019-01957-8 [15] Chryssanthakis P, Barton N, Lorig L, et al. Numerical simulation of fiber reinforced shotcrete in a tunnel using the discrete element method. Int J Rock Mech Min Sci, 1997, 34(3-4): 54.e1 [16] Huang F, Wang Y, Wen Y B, et al. The deformation and failure analysis of rock mass around tunnel by coupling finite difference method and discrete element method. Indian Geotech J, 2019, 49(4): 421 doi: 10.1007/s40098-018-0348-9 [17] Yang Z M, Wu S C, Gao Y T, et al. Time and technique of rehabilitation for large deformation of tunnels in jointed rock masses based on FDM and DEM numerical modeling. Tunn Undergr Space Technol, 2018, 81: 669 doi: 10.1016/j.tust.2018.08.036 [18] Saiang D. Stability analysis of the blast-induced damage zone by continuum and coupled continuum-discontinuum methods. Eng Geol, 2010, 116(1-2): 1 doi: 10.1016/j.enggeo.2009.07.011 [19] Lisjak A, Grasselli G, Vietor T. Continuum-discontinuum analysis of failure mechanisms around unsupported circular excavations in anisotropic clay shales. Int J Rock Mech Min Sci, 2014, 65: 96 doi: 10.1016/j.ijrmms.2013.10.006 [20] Liu Q S, Xu X Y, Wu Z J. A GPU-based numerical manifold method for modeling the formation of the excavation damaged zone in deep rock tunnels. Comput Geotech, 2020, 118: 103351 doi: 10.1016/j.compgeo.2019.103351 [21] Wang Y N, Zhao M H, Li S H, et al. Stochastic structural model of rock and soil aggregates by continuum-based discrete element method. Sci China Ser E-Technol Sci, 2005, 48(1): 95 [22] Feng C, Li S H, Liu X Y, et al. A semi-spring and semi-edge combined contact model in CDEM and its application to analysis of Jiweishan landslide. J Rock Mech Geotech Eng, 2014, 6(1): 26 doi: 10.1016/j.jrmge.2013.12.001 [23] Cheng A H D. Poroelasticity. Switzerland: Springer International Publishing, 2016 -
點擊查看大圖
圖(20) / 表(1)
計量
- 文章訪問數: 423
- HTML全文瀏覽量: 170
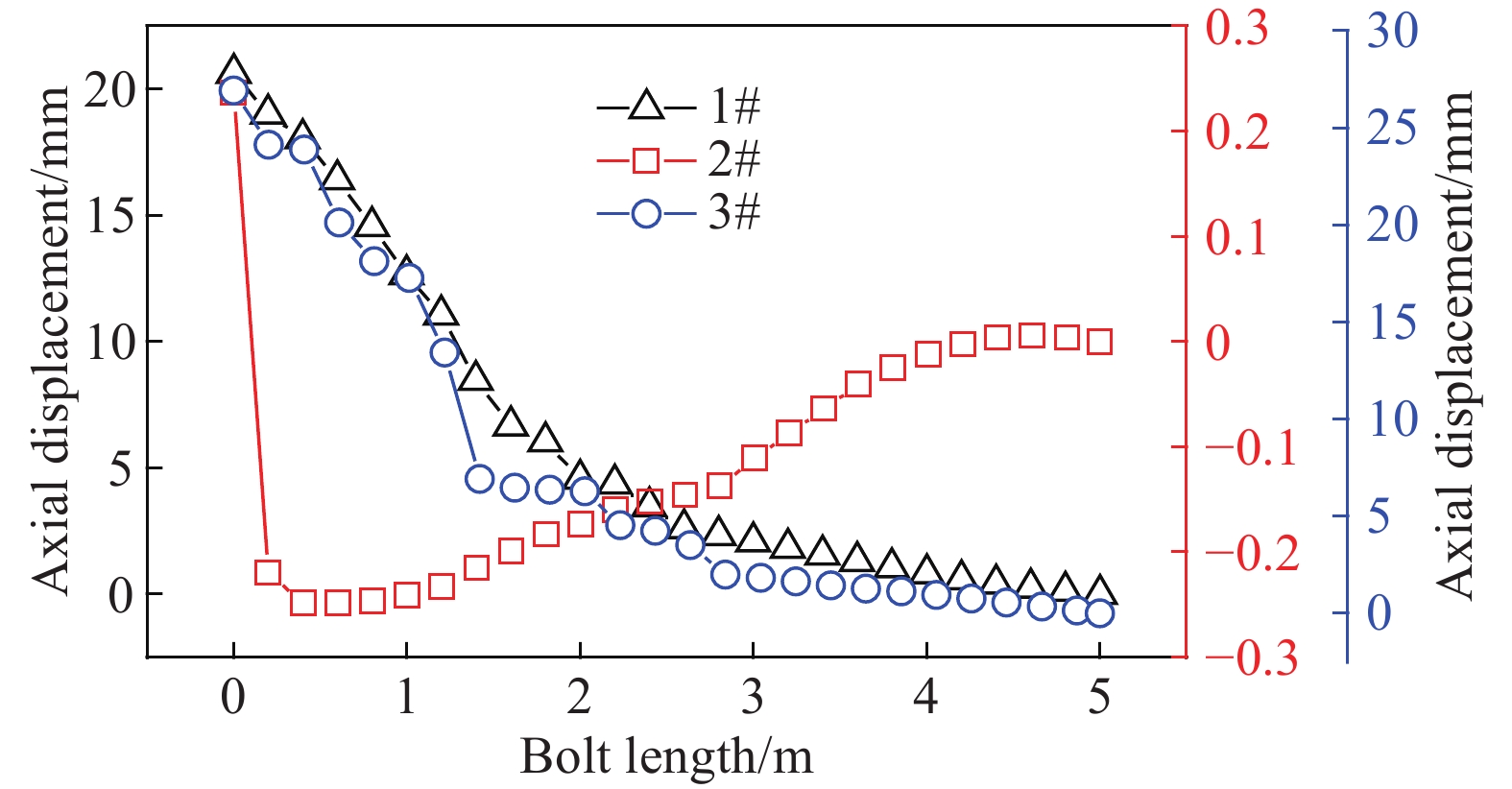
- PDF下載量: 86
- 被引次數: 0
