Phase field method study on the directional solidification microstructure of a Fe–C alloy under forced convection
-
摘要: 定向凝固技術能夠獲得特定柱狀晶結構，對于優化合金軸向力學性能具有非常顯著的效果。本文采用耦合流場的相場模型模擬了定向凝固過程中枝晶的生長過程，研究了各向異性系數、界面能對定向凝固枝晶生長的影響以及強制對流作用下枝晶的生長行為。數值求解過程中，選用基于均勻網格的有限差分方法對控制方程進行離散，實現了格子中標記點算法（MAC）和相場離散計算方法的聯合求解。處理微觀速度場和壓力場耦合時，采用MAC算法求解Navier-Stokes方程和壓力Poisson方程，采用交錯網格法處理復雜的自由界面。結果表明：隨著各向異性系數的增大，枝晶尖端生長速度增大，曲率半徑減小，枝晶根部溶質濃度逐漸降低；隨著界面能的增大，枝晶尖端曲率半徑增大，當界面能為最大（0.6 J·m?2）時，凝固呈現平界面的凝固方式向前推進；強迫對流對定向凝固枝晶生長方向影響較大，上游方向定向凝固枝晶粗大且生長速度更快，其現象隨流速的增大而愈加明顯。Abstract: A specific columnar crystal structure is obtained using the directional solidification technique, which has a substantial effect on the optimization of the axial mechanical properties of the alloy. Additionally, the convection phenomenon in the melt changes the temperature field and concentration field at the front of the solid–liquid interface, affecting the shape of this interface. Thus, the influence on alloy properties cannot be ignored. Although the phase field method has more research on the microdendrite growth morphology, the results of coupling the flow field into the phase field and exploring the microdendrite morphology of directional solidification are still scarce. In this paper, the phase field model of a coupled flow field is used to simulate dendritic growth during directional solidification. The effects of the anisotropy coefficient and interfacial energy on the growth of directionally solidified dendrites and the growth behavior of dendrites under forced convection were studied. For the numerical solution procedure, a uniform grid of the finite difference method was used to discretize the governing equations. A combined solution of the MAC algorithm and a phase field discrete calculation was realized. When addressing the coupling of the microvelocity and pressure fields, the MAC algorithm was used to solve the Navier–Stokes equation and pressure Poisson equation, and the interlocked grid method was applied to handle the complex free interface. The results show that the growth rate of the dendrite tip increases, and the radius of curvature and the solute concentration at the root of the dendrite decrease with an increasing anisotropy coefficient. When the anisotropy coefficient is a maximum of 0.065, the wall of the dendrite tends to develop toward a secondary dendrite because of the influence of the anisotropy coefficient; with increasing interfacial energy, the radius of curvature of the dendrite tip increases. When the interfacial energy is a maximum of 0.6 J·m?2, the solidification shows a flat interface advancing mode; forced convection has a great influence on the growth direction of directional solidification dendrites. The directional solidification of dendrites in the upstream direction is coarse and grows faster with increasing flow rate. Additionally, the dendrite growth morphology observed using an optical microscope agrees well with the experimental results.
-
Key words:
- Fe–C alloys /
- directional solidification /
- phase field method /
- convection /
- columnar dendrite
-
圖 2 相場與溶質場模擬結果. (a) 相場; (b) 溶質場; (c) Fe?C合金定向凝固柱狀枝晶形態
Figure 2. Simulation results of the phase and solute fields: (a) phase field; (b) solute field; (c) directional solidification columnar dendritic morphology of the Fe–C alloy
圖 3 各向異性系數對定向凝固柱狀晶組織的影響. (a) 各向異性系數0.04; (b) 各向異性系數0.05; (c) 各向異性系數0.065
Figure 3. Effect of the anisotropy coefficient on the directionally solidified columnar crystal structure: (a) anisotropy coefficient of 0.04; (b) anisotropy coefficient of 0.05; (c)anisotropy coefficient of 0.065
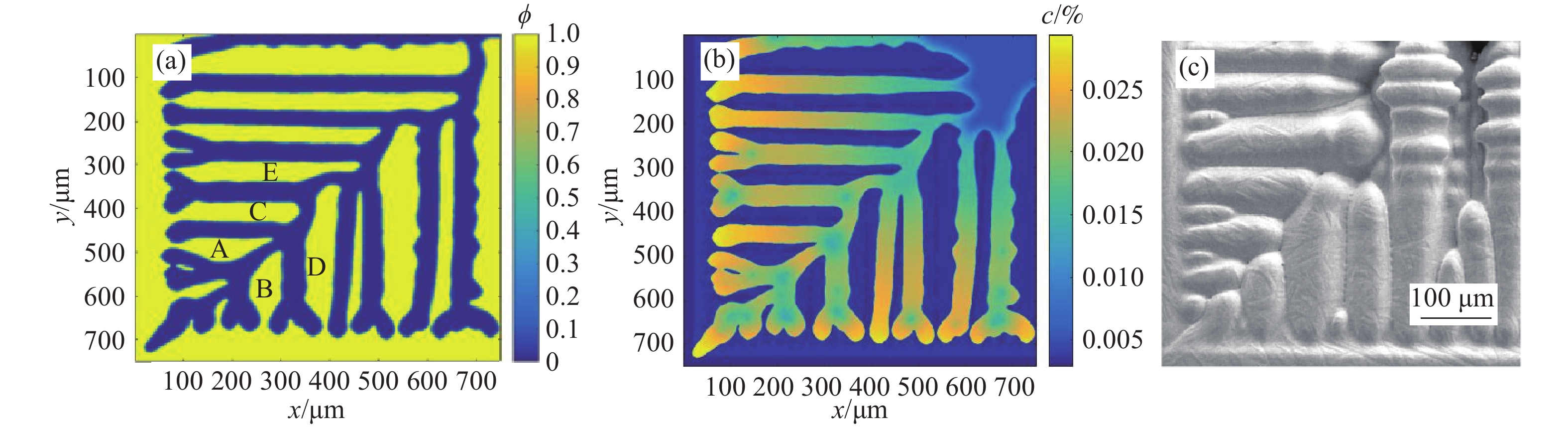
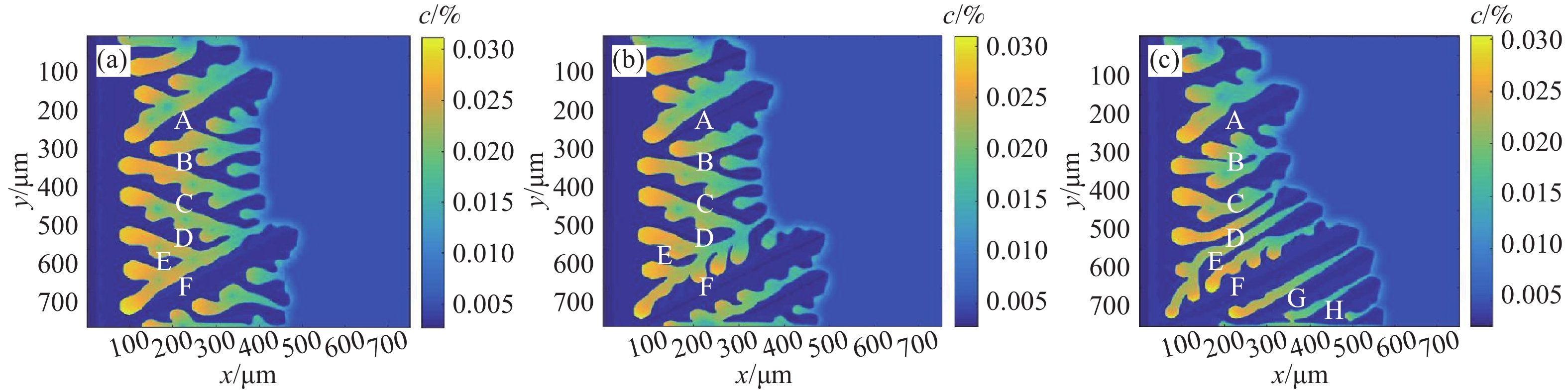
圖 4 實驗觀察Fe?C合金定向凝固柱狀枝晶生長形態SEM圖. (a) 弱各向異性系數; (b) 強各向異性系數（小過冷度）; (c) 強各向異性系數（大過冷度）
Figure 4. Growth morphology of the columnar dendrite of the Fe–C alloy during directional solidification observed using scanning electron microscopy: (a) weak anisotropy coefficient; (b) strong anisotropy coefficient (low undercooling); (c) strong anisotropy coefficient (high undercooling)
圖 5 同一計算步長下不同各向異性系數的平均枝晶尺寸及直徑變化圖
Figure 5. Variation in the average dendrite size and diameter with different anisotropy coefficients at the same calculation step
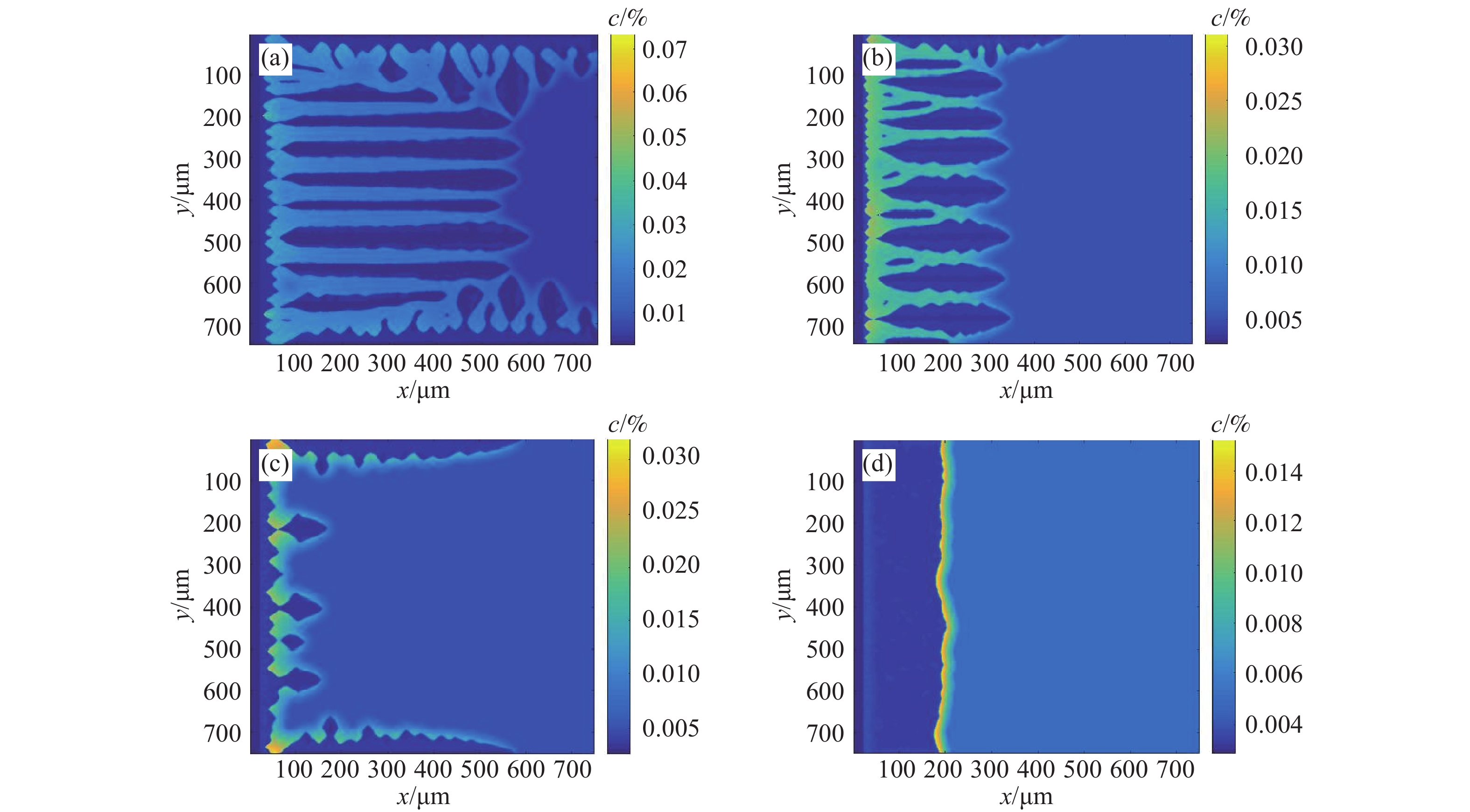
圖 6 界面能對定向凝固柱狀枝晶組織的影響. (a) 界面能為0.3 J·m?2; (b) 界面能為0.35 J·m?2; (c) 界面能為0.45 J·m?2; (d) 界面能為0.6 J·m?2
Figure 6. Effect of the interfacial energy on the directionally solidified columnar dendrite structure: (a) interfacial energy of 0.3 J·m?2; (b) interfacial energy of 0.35 J·m?2; (c) interfacial energy of 0.45 J·m?2; (d) interfacial energy of 0.6 J·m?2
圖 7 對流作用下枝晶生長的相場與溶質場模擬結果. (a) 相場; (b) 溶質場
Figure 7. Simulation results of the phase and solute fields of dendritic growth under convection: (a) phase field; (b) solute field
圖 8 不同微觀對流速度下的枝晶生長形貌. (a) 對流速度0.02 m·s?1; (b) 對流速度0.08 m·s?1; (c) 對流速度0.1 m·s?1
Figure 8. Dendrite growth morphology under different microconvection velocities: (a) convective velocity of 0.02 m·s?1; (b) convective velocity of 0.08 m·s?1; (c) convective velocity of 0.1 m·s?1
表 1 Fe-C合金熱力學參數
Table 1. Thermophysical data for dilute Fe?C alloy
Solute mass fraction of carbon/% ${\rm{ \sigma }}/({\rm{J}} \cdot {{\rm{m}}^{ - 2} })$ ${T_m}/{\rm{K}}$ ${V_m}/({{\rm{m}}^3} \cdot {\rm{mol}}^{ - 1} )$ ${k^{\rm{e}}}$ ${D_{\rm{L}}}/({{\rm{m}}^2} \cdot {{\rm{s}}^{ - 1} })$ ${D_{\rm{S}}}/({{\rm{m}}^2} \cdot {{\rm{s}}^{ - 1} })$ ${m^{\rm{e} } }$ 0.5 0.204 1810 7.7 × 10?6 0.204 2×10?8 6×10?9 ?1836 
下載: 導出CSV
www.77susu.com<span id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> <span id="fpn9h"><noframes id="fpn9h"> <th id="fpn9h"></th> <strike id="fpn9h"><noframes id="fpn9h"><strike id="fpn9h"></strike> <th id="fpn9h"><noframes id="fpn9h"> <span id="fpn9h"><video id="fpn9h"></video></span> <ruby id="fpn9h"></ruby> <strike id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> -
參考文獻
[1] Ding X F, Lin J P, Zhang L Q, et al. Lamellar orientation control in a Ti?46Al?5Nb alloy by directional solidification. Scr Mater, 2011, 65(1): 61 doi: 10.1016/j.scriptamat.2011.02.011 [2] Wen Y G, Cui C J, Tian L L, et al. Research progress and application of the directional solidification technology. Mater Rep, 2016, 30(3): 116問亞崗, 崔春娟, 田露露, 等. 定向凝固技術的研究進展與應用. 材料導報, 2016, 30(3):116 [3] Liu S C, Liu L H, Li S, et al. Free dendritic growth model considering both interfacial nonisothermal nature and effect of convection for binary alloy. Trans Nonferrous Met Soc China, 2021, 31(5): 1518 doi: 10.1016/S1003-6326(21)65595-4 [4] Tourret D, Karma A. Growth competition of columnar dendritic grains: A phase-field study. Acta Mater, 2015, 82: 64 doi: 10.1016/j.actamat.2014.08.049 [5] Takaki T, Shimokawabe T, Ohno M, et al. Unexpected selection of growing dendrites by very-large-scale phase-field simulation. J Cryst Growth, 2013, 382: 21 [6] Shibuta Y, Ohno M, Takaki T. Advent of cross‐scale modeling: high‐performance computing of solidification and grain growth. Adv Theory Simul, 2018, 1(9): 1800065 doi: 10.1002/adts.201800065 [7] Aufgebauer H, Kundin J, Emmerich H, et al. Phase-field simulations of particle capture during the directional solidification of silicon. J Cryst Growth, 2016, 446: 12 doi: 10.1016/j.jcrysgro.2016.04.032 [8] Ferreira A F, Castro J A, Ferreira L. Predicting secondary-dendrite arm spacing of the Al?4.5wt%Cu alloy during unidirectional solidification. Mat Res, 2016, 20(1): 68 [9] Kundin J, Siquieri R, Emmerich H. A quantitative multi-phase-field modeling of the microstructure evolution in a peritectic Al?Ni alloy. Phys D-Nonlinear Phenom, 2013, 243(1): 116 doi: 10.1016/j.physd.2012.10.004 [10] Novokreshchenova A A, Lebedev V G. Determining the phase-field mobility of pure nickel based on molecular dynamics data. Tech Phys, 2017, 62(4): 642 doi: 10.1134/S1063784217040181 [11] Pinomaa T, Provatas N. Quantitative phase field modeling of solute trapping and continuous growth kinetics in quasi-rapid solidification. Acta Mater, 2019, 168: 167 doi: 10.1016/j.actamat.2019.02.009 [12] Lenart R, Eshraghi M. Modeling columnar to equiaxed transition in directional solidification of Inconel 718 alloy. Comput Mater Sci, 2020, 172: 109374 [13] Enugala S N, Kellner M, Kobold R, et al. Theoretical and numerical investigations of rod growth of an Ni?Zr eutectic alloy. J Mater Sci, 2019, 54(19): 12605 doi: 10.1007/s10853-019-03802-3 [14] Noubary K D, Kellner M, Steinmetz P, et al. Phase-field study on the effects of process and material parameters on the tilt angle during directional solidification of ternary eutectics. Comput Mater Sci, 2017, 138: 403 [15] Steinmetz P, Kellner M, H?tzer J, et al. Quantitative comparison of ternary eutectic phase-field simulations with analytical 3D Jackson–hunt approaches. Metall Mater Trans B, 2018, 49(1): 213 [16] Ghosh S, Karma A, Plapp M, et al. Influence of morphological instability on grain boundary trajectory during directional solidification. Acta Mater, 2019, 175: 214 doi: 10.1016/j.actamat.2019.04.054 [17] Wang Z J, Wang J C, Li J J, et al. Quantitative investigation of cellular growth in directional solidification by phase-field simulation. Phys Rev E, 2011, 84(4): 041604 [18] Wang Z J, Li J J, Wang J C, et al. Phase field modeling the selection mechanism of primary dendritic spacing in directional solidification. Acta Mater, 2012, 60(5): 1957 [19] Chen M, Hu X D, Ju D Y, et al. The microstructure prediction of magnesium alloy crystal growth in directional solidification. Comput Mater Sci, 2013, 79: 684 doi: 10.1016/j.commatsci.2013.07.030 [20] Yang C, Xu Q Y, Liu B C. GPU-accelerated three-dimensional phase-field simulation of dendrite growth in a nickel-based superalloy. Comput Mater Sci, 2017, 136: 133 doi: 10.1016/j.commatsci.2017.04.031 [21] Chen Y, Bogno A A, Xiao N M, et al. Quantitatively comparing phase-field modeling with direct real time observation by synchrotron X-ray radiography of the initial transient during directional solidification of an Al?Cu alloy. Acta Mater, 2012, 60(1): 199 [22] Wang Y B, Jia S S, Wei M G, et al. Coupling in situ synchrotron X-ray radiography and phase-field simulation to study the effect of low cooling rates on dendrite morphology during directional solidification in Mg?Gd alloys. J Alloys Compd, 2020, 815: 152385 [23] Zhang B, Zhao Y H, Chen W P, et al. Phase field simulation of dendrite sidebranching during directional solidification of Al?Si alloy. J Cryst Growth, 2019, 522: 183 doi: 10.1016/j.jcrysgro.2019.06.027 [24] Zhu C S, Xu S, Feng L, et al. Phase-field model simulations of alloy directional solidification and seaweed-like microstructure evolution based on adaptive finite element method. Comput Mater Sci, 2019, 160: 53 doi: 10.1016/j.commatsci.2018.12.058 [25] Wang Y B, Wei M G, Liu X T, et al. Phase-field study of the effects of the multi-controlling parameters on columnar dendrite during directional solidification in hexagonal materials. Eur Phys J E Soft Matter, 2020, 43(7): 41 doi: 10.1140/epje/i2020-11964-9 [26] Xia Y, Li L, Wang P, et al. Characteristics of the as-cast high-carbon microalloyed continuous casting bloom steel for expansion-break connecting rods. Chin J Eng, 2022, 44(2): 189 doi: 10.3321/j.issn.1001-053X.2022.2.bjkjdxxb202202004夏勇, 李亮, 王璞, 等. 脹斷連桿用高碳微合金鋼連鑄大方坯的鑄態組織. 工程科學學報, 2022, 44(2):189 doi: 10.3321/j.issn.1001-053X.2022.2.bjkjdxxb202202004 [27] Yuan X F, Ding Y T. Phase-field method of multi-dendrites growth under forced flow. J Mater Eng, 2011, 39(10): 5 doi: 10.3969/j.issn.1001-4381.2011.10.002袁訓鋒, 丁雨田. 強制對流作用下多枝晶生長的相場法研究. 材料工程, 2011, 39(10):5 doi: 10.3969/j.issn.1001-4381.2011.10.002 [28] Yuan X F, Ding Y T. Simulation of dendritic growth of pure Ni using phase-field model under forced flow Ⅱ. Foundry Technol, 2012, 33(9): 1034袁訓鋒, 丁雨田. 強制對流作用下純Ni枝晶生長的相場法研究(二). 鑄造技術, 2012, 33(9):1034 [29] Chen Z, Hao L M, Chen C L. Simulation of faceted dendrite growth of non-isothermal alloy in forced flow by phase field method. J Cent South Univ Technol, 2011, 18(6): 1780 doi: 10.1007/s11771-011-0902-4 [30] Wang J W, Wang Z P, Lu Y, et al. Effect of forced lamina flow on microsegregation simulated by phase field method quantitatively. Trans Nonferrous Met Soc China, 2012, 22(2): 391 [31] Zhu C S, Lei P, Xiao R Z, et al. Phase-field modeling of dendritic growth under forced flow based on adaptive finite element method. Trans Nonferrous Met Soc China, 2015, 25(1): 241 doi: 10.1016/S1003-6326(15)63599-3 [32] Luo S, Wang P, Wang W L, et al. PF-LBM modelling of dendritic growth and motion in an undercooled melt of Fe?C binary alloy. Metall Mater Trans B, 2020, 51(5): 2268 doi: 10.1007/s11663-020-01925-6 [33] Zhang A, Du J L, Guo Z P, et al. Phase-field lattice-Boltzmann investigation of dendritic evolution under different flow modes. Philos Mag, 2019, 99(23): 2920 [34] Takaki T, Sakane S, Ohno M, et al. Competitive growth during directional solidification of a binary alloy with natural convection: Two-dimensional phase-field study. Modelling Simul Mater Sci Eng, 2019, 27(5): 054001 doi: 10.1088/1361-651X/ab1a17 [35] Chen Z, Chen C L, Hao L M. Phase field simulation of the interface morphology during directional solidification in a forced flow/free flow. Rare Met Mater Eng, 2010, 39(12): 2117陳志, 陳長樂, 郝麗梅. 有/無強制流動下定向凝固界面形貌的數值模擬研究. 稀有金屬材料與工程, 2010, 39(12):2117 [36] Yang C, Xu Q Y, Liu B C. Phase-field-lattice Boltzmann simulation of dendrite growth under natural convection in multicomponent superalloy solidification. Rare Met, 2020, 39(2): 147 doi: 10.1007/s12598-019-01292-5 [37] Kim S G, Kim W T, Suzuki T. Phase-field model for binary alloys. Phys Rev E, 1999, 60(6): 7186 doi: 10.1103/PhysRevE.60.7186 [38] Huang D L. A Course in Computational Fluid Dynamics. Beijing: Higher Education Press, 2010張德良. 計算流體力學教程. 北京: 高等教育出版社, 2010 [39] Liu J L, Lv Y Q, Xu B. Two dimensional debris flow numerical calculation model based on MacCormack-TVD finite difference algorithm. Bull Sci Technol, 2019, 35(4): 222 doi: 10.13774/j.cnki.kjtb.2019.04.040劉建麟, 呂義清, 徐博. 基于MacCormack-TVD有限差分算法的二維泥石流數值計算模型. 科技通報, 2019, 35(4):222 doi: 10.13774/j.cnki.kjtb.2019.04.040 [40] Su Y Q, Luo L S. Directional Solidification of Peritectic Alloys. Harbin: Harbin Institute of Technology Press, 2017蘇彥慶, 駱良順. 包晶合金定向凝固. 哈爾濱: 哈爾濱工業大學出版社, 2017 [41] Wang J C, Guo C W, Li J J, et al. Recent progresses in competitive grain growth during directional solidification. Acta Metall Sin, 2018, 54(5): 657 doi: 10.11900/0412.1961.2017.00543王錦程, 郭春文, 李俊杰, 等. 定向凝固晶粒競爭生長的研究進展. 金屬學報, 2018, 54(5):657 doi: 10.11900/0412.1961.2017.00543 -
點擊查看大圖
圖(8) / 表(1)
計量
- 文章訪問數: 662
- HTML全文瀏覽量: 231
- PDF下載量: 73
- 被引次數: 0
