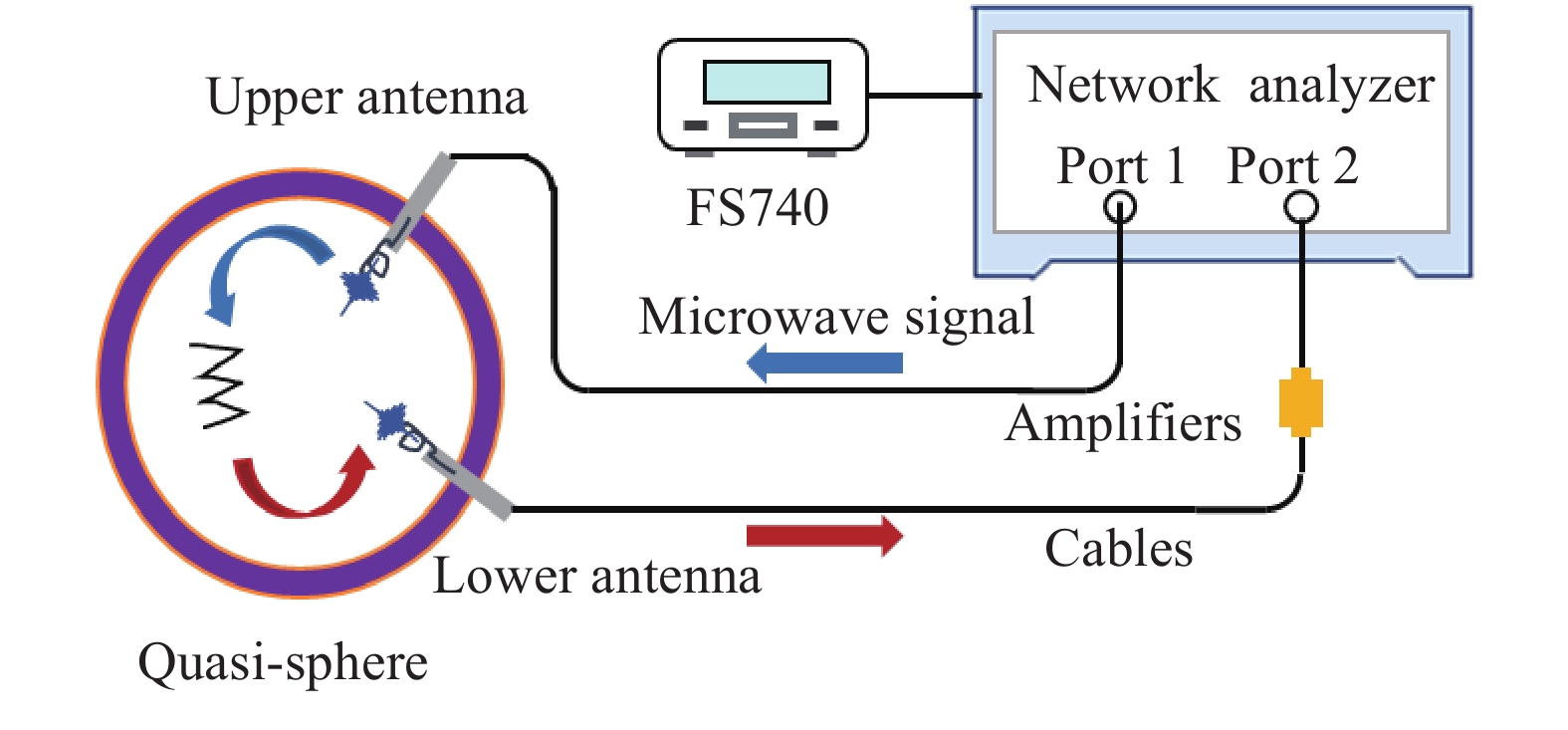
In situ evaluation of the linear thermal expansion coefficient of Cu-ETP from 4.3 K to 299 K
-
摘要: 采用多模式微波諧振法,開展了定壓氣體折射率基準測溫系統中諧振腔材料電解精煉韌銅(Cu-ETP)線性熱膨脹系數的高精度原位實驗測量及其不確定度分析研究,溫度范圍為4.3~299 K。針對不同的溫度區間,采用了降溫法(5~299 K)和控溫法(4.3~26 K)兩種實驗測量方案,通過降溫法測得的線性熱膨脹系數標準不確定度優于2.2×10?7 K?1,其中,重復性是其測量不確定度的主要來源;通過控溫法測得的線性熱膨脹系數標準不確定度優于2.9×10?9 K?1,微波模式一致性和重復性是其測量不確定度的兩大主要來源。由于控溫穩定性高、微波測量噪聲低,控溫法所獲得的線性熱膨脹系數結果更為精確。最后,按照溫區范圍進一步發展了該系統內Cu-ETP材料線性熱膨脹系數的計算方程,實現了實驗數據與溫度的高精度關聯。Abstract: In this study, the linear thermal expansion coefficient of electrolytic through pitch copper (Cu-ETP) was used as a resonator material in the single-pressure refractive-index gas thermometer and was evaluated in situ at high precision via the multi-mode microwave resonance method in the temperature range of 4.3 to 299 K. Two experimental measurement schemes, cooling method (5–299 K) and temperature control method (4.3–26 K), are employed for different temperature ranges. These methods adopt the same calculation method, wherein the relation between the length and temperature is obtained first, and then the polynomial fitting is used to obtain the linear thermal expansion coefficient of the resonator. The resonator installed in the cryostat has a quasi–spherical shape, with similar radii in the x, y, and z axes; for example, if the radius in one direction is R, then the radii in the other two directions are 1.001R and 1.0005R. The accurate radius of the quasi–sphere in low temperature can be measured by the multi-mode microwave resonance method, which is a mature method with a significant non-ideal correction to reduce the difference between the actual and ideal environments. For the cooling method, to reduce the impact of random errors, we collect five microwave modes (TM11, TE11, TM12, TE12, and TE13) and repeat four experiment runs (Run9, Run10, Run12, and Run17), assuming the average value as the final result. The max radius deviation during the different modes is 0.37 μm, indicating that the result has a good mode consistency. Then, the measurement uncertainty of the radius is analyzed, with all values within 0.27 μm and the mode consistency being the main influencing item. The linear thermal expansion coefficient can be calculated by the polynomial fitting method with the standard uncertainty of 2.2×10?7 K?1, with repeatability being the main source of uncertainty. As for the controlling method, the same analyzing procedure is implemented, the max deviation of the radius during the four modes (TM11, TE11, TM12, and TE13) is 0.12 μm, and the deviation of different runs from the average value is within 0.0056 μm, smaller than the radius uncertainty, which has good repeatability. The standard uncertainty of radius is within 0.12 μm in the entire range and the non-ideal correction and frequency stability are the two main influencing factors. The standard uncertainty of the linear thermal expansion is 2.9×10?9 K?1, and the two main sources are the microwave mode consistency and repeatability. Due to the higher stability of temperature control and lower microwave measurement noise, the results determined by the temperature control method are more accurate. Finally, equations for the linear thermal expansion coefficient of Cu-ETP are further developed to realize a high-precision correlation between the experimental data and temperature.
-
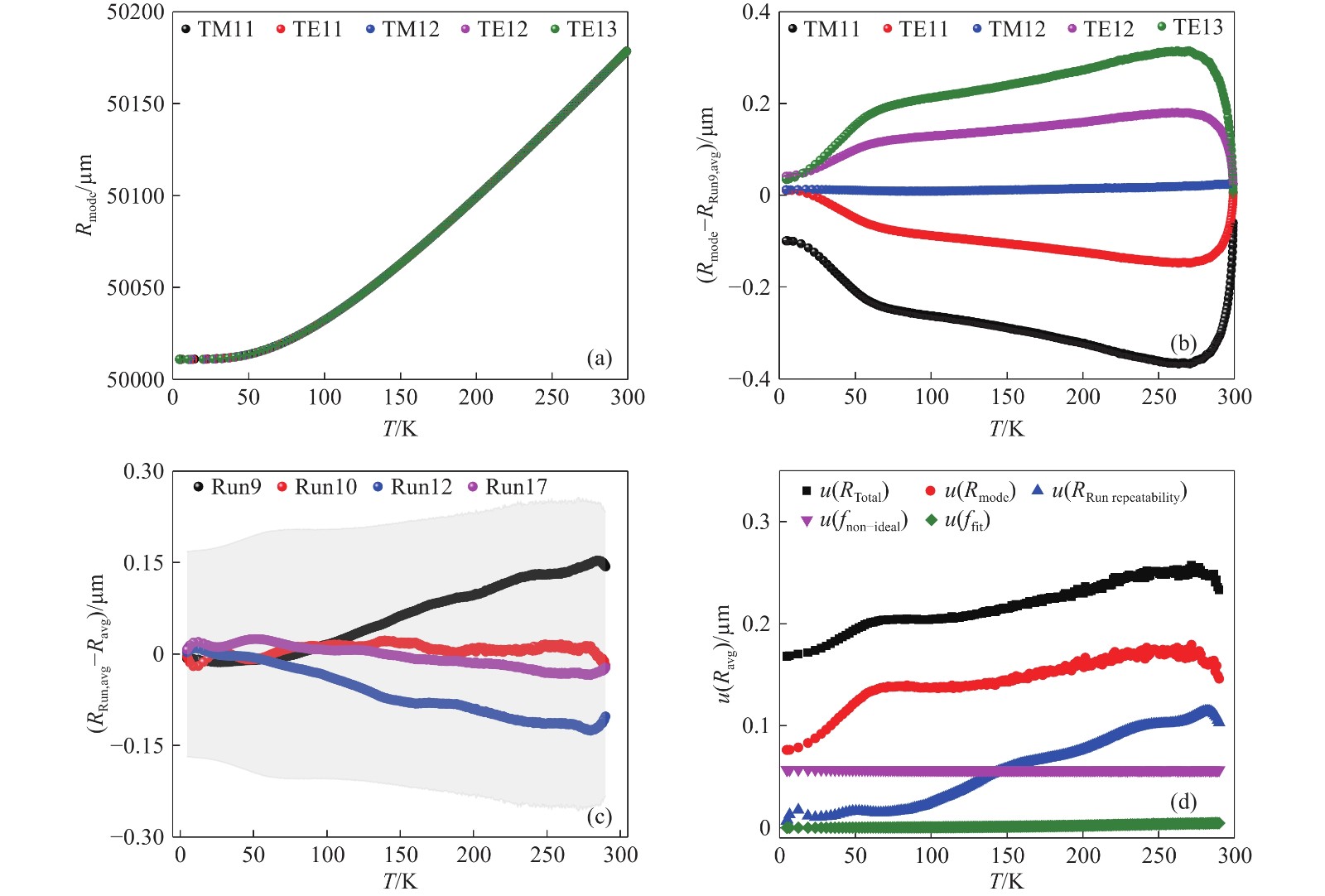
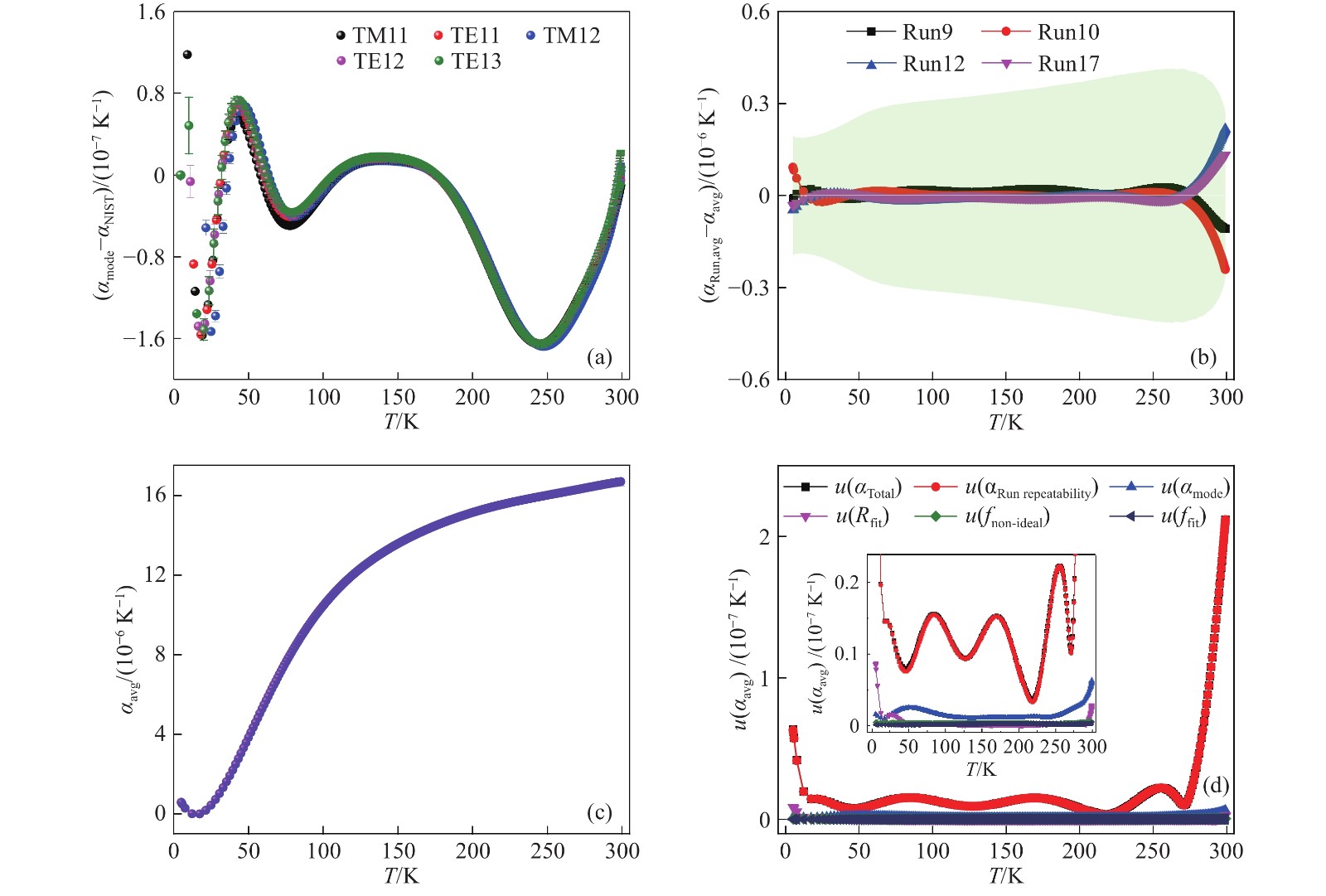
圖 4 降溫過程中的諧振腔半徑計算結果分析. (a) Run9單個微波模式測得的半徑; (b) Run9單個微波模式測得的半徑與平均半徑的偏差; (c) 不同輪實驗測得的半徑平均值與最終半徑平均值的偏差(灰色背景為半徑平均值的標準不確定度誤差帶); (d) 降溫過程中最終半徑平均值的不確定度分析
Figure 4. Analysis of the resonator radius during cooling: (a) radius of each microwave mode of Run9; (b) deviation of the single microwave mode and the average radius of Run9; (c) radius deviation in different runs and the average value (the gray background is the error bar of the standard uncertainty in the average radius value); (d) uncertainty analysis of the final average radius during cooling
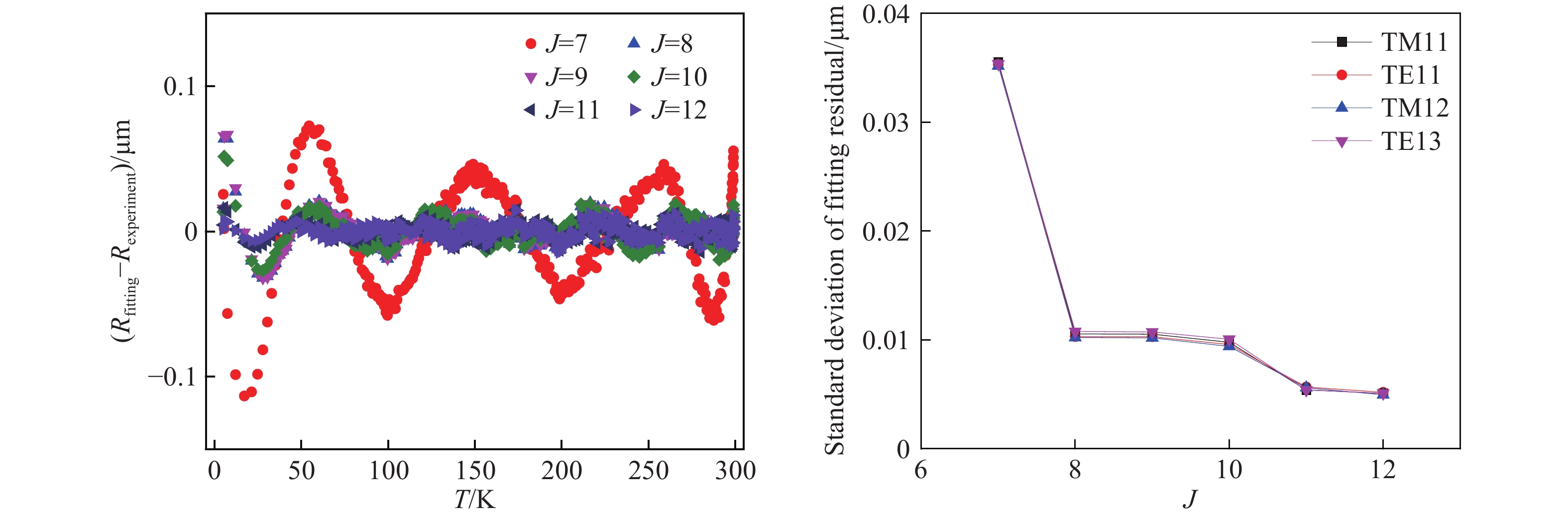
圖 5 不同擬合階數的擬合結果. (a) 不同擬合階數下半徑實驗值與擬合值相對偏差的變化; (b) 不同擬合階數下擬合殘差標準差的變化
Figure 5. Fitting result of different fitting sequences: (a) deviation of the experimental and fitting values of the radius with different fitting order; (b) change of standard deviation of the fitting residual with different fitting order
圖 6 Run9降溫過程中線性熱膨脹系數計算結果分析. (a) 各微波模式線性熱膨脹系數計算值和文獻值的偏差; (b) 不同輪實驗線性熱膨脹系數平均值與最終平均值的偏差; (c) 不同輪線性熱膨脹系數的最終平均值; (d) 線性熱膨脹系數的不確定度分析
Figure 6. Analysis of the linear thermal expansion during the cooling of Run9: (a) deviation of linear thermal expansion of every microwave mode and the literature value; (b) deviation of the linear thermal expansions of different runs and the final average value; (c) final average value of the linear thermal expansion of different runs; (d) uncertainty analysis of the linear thermal expansion
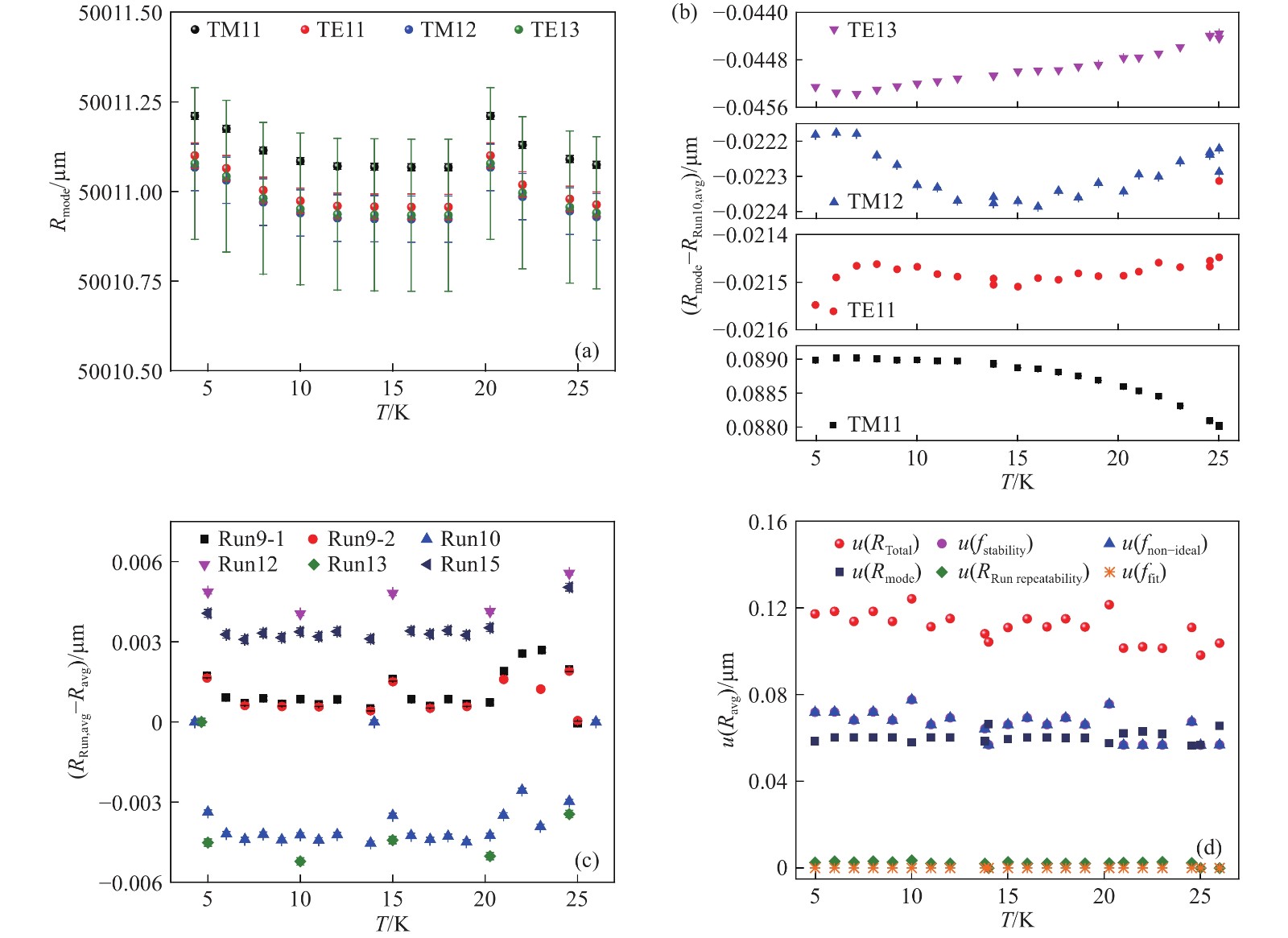
圖 7 控溫過程中諧振腔半徑計算結果分析. (a) Run10控溫過程中各微波模式諧振腔半徑計算結果; (b) Run10控溫過程單個微波模式半徑和平均半徑的偏差; (c) 各輪控溫過程中半徑各模式平均值和最終平均半徑值的偏差; (d) 控溫過程中半徑的不確定度分析
Figure 7. Analysis of the resonator radius during temperature control: (a) resonator radii of different microwave modes in Run10; (b) deviation of single microwave mode and average radius in Run10; (c) deviation of the average radii of different modes in different runs and the final average value; (d) uncertainty analysis of the resonator radius
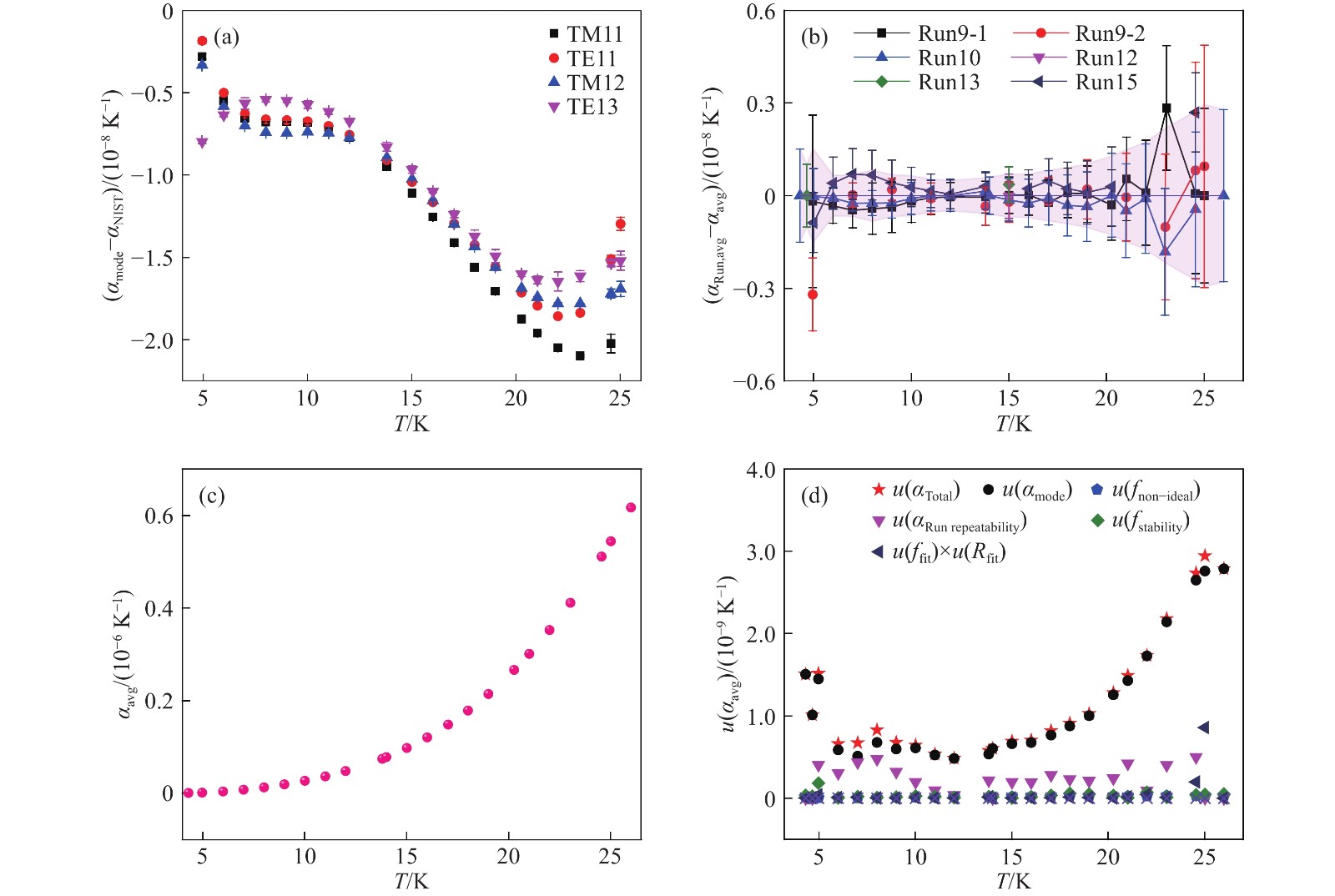
圖 8 控溫過程中線性熱膨脹系數計算結果分析. (a) Run10實驗中各微波模式線性熱膨脹系數計算結果與文獻值的偏差; (b) 不同輪實驗線性熱膨脹系數平均值和最終平均值的偏差(粉色背景為平均值的標準不確定度誤差帶); (c) 多輪控溫過程中線性熱膨脹系數的最終平均值; (d) 控溫過程中線性熱膨脹系數的不確定度分量占比
Figure 8. Analysis of the linear thermal expansion during temperature control: (a) deviation of experiment and reported linear thermal expansion of Run10 for microwave different modes; (b) deviation of average thermal expansion for different runs and the final average value (the pink background is the error bar of the standard uncertainty of the final average value); (c) final average value of linear thermal expansion for different runs; (d) uncertainty analysis of the final linear thermal expansion
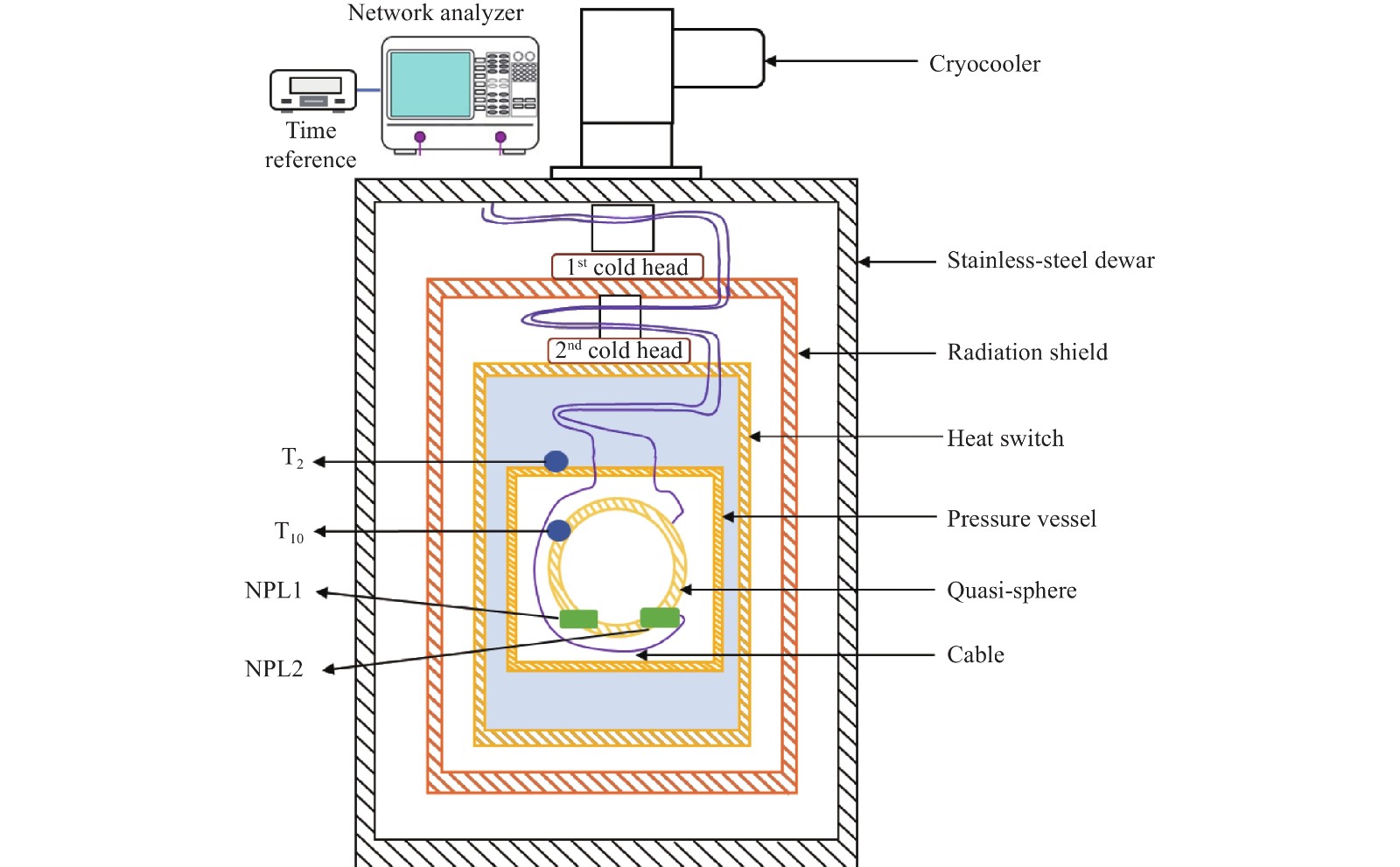
表 1 本裝置中的儀表信息
Table 1. Instrument information in this cryostat
Name Brand Typical accuracy Network Analyzer [32] Keysight 0.5×10?6 Hz* 2002 multimeter [33] Keithley 0.0006% AC resistance bridge
(ASLF900) [34]ASL 0.01 mK Cernox sensor
(CX-1050?
CU-HT?1.4L) [35]Lakeshore 4.2–10 K: ±5 mK
10–20 K: ±6 mK
20–30 K: ±9 mKRIRT censor
(NPL-calibrated)—
NPL1&NPL2 [36]Tinsley 5 K: 0.26 mK
26 K: 0.47 mKNote: *In this paper, GPS/GNSS time or frequency standard system (FS740) is used as the frequency reference, and the frequency measurement accuracy can reach the order of from 10?9 to 10?12. 表 2 5、15和24.5 K下準球形諧振腔半徑的不確定度分析
Table 2. Uncertainty analysis of the radius at 5, 15, and 24.5 K
Source u(R) / μm T = 5 K T = 15 K T = 24.5 K Frequency fitting 2.76×10?5 3.38×10?5 3.23×10?5 Frequency stability 0.072 0.066 0.067 Nonideal correction 0.071 0.065 0.066 Mode consistency 0.058 0.059 0.056 Run repeatability 0.0025 0.0027 0.0023 Total uncertainty 0.12 0.11 0.11 表 3 5、15和24.5 K下線性熱膨脹系數不確定度分析
Table 3. Uncertainty analysis of linear thermal expansion at 5, 15, and 24.5 K
Source u(α) / (10?9 K?1) T = 5 K T = 15 K T = 24.5 K Frequency fitting 0.042 0.0047 0.19 Frequency stability 0.18 0.0032 0.41 Nonideal correction 0.0058 0.019 0.029 Mode consistency 1.45 0.66 2.65 Run repeatability 0.40 0.20 0.50 Radius fitting 1.93×10?7 7.52×10?7 2.95×10?7 Total uncertainty 1.5 0.69 2.7 www.77susu.com<span id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> <span id="fpn9h"><noframes id="fpn9h"> <th id="fpn9h"></th> <strike id="fpn9h"><noframes id="fpn9h"><strike id="fpn9h"></strike> <th id="fpn9h"><noframes id="fpn9h"> <span id="fpn9h"><video id="fpn9h"></video></span> <ruby id="fpn9h"></ruby> <strike id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> -
參考文獻
[1] Phillips W D. The end of artefacts. Nat Phys, 2019, 15(5): 518 [2] Consultative Committee for Time and Frequency. Mise en pratique for the definition of the second in the SI [Z/OL]. Sciencepaper Online (2019-05-20) [2021-12-03].https://www.bipm.org/utils/en/pdf/si-mep/SI-App2-second.pdf [3] Gaiser C, Fellmuth B, Haft N. Primary thermometry from 2.5 K to 140 K applying dielectric-constant gas thermometry. Metrologia, 2017, 54(1): 141 doi: 10.1088/1681-7575/aa5389 [4] Pitre L, Sparasci F, Risegari L, et al. New measurement of the Boltzmann constantkby acoustic thermometry of helium-4 gas. Metrologia, 2017, 54(6): 856 doi: 10.1088/1681-7575/aa7bf5 [5] Rourke P M C, Gaiser C, Gao B, et al. Refractive-index gas thermometry. Metrologia, 2019, 56(3): 032001 doi: 10.1088/1681-7575/ab0dbe [6] Gao B, Pitre L, Luo E C, et al. Feasibility of primary thermometry using refractive index measurements at a single pressure. Measurement, 2017, 103: 258 doi: 10.1016/j.measurement.2017.02.039 [7] Simon N J, Drexler E S, Reed R P. Properties of copper and copper alloys at cryogenic temperatures [R/OL]. Sciencepaper Online (1992-02-01) [2021-12-03].https://www.osti.gov/servlets/purl/5340308 [8] Guo Y L. CIVA Simulation and Experimental Study of Eddy Current Array Detection Aluminum Sheet [Dissertation]. Nanchang: Nanchang Hangkong University, 2014郭永良. 渦流陣列檢測鋁薄板的CIVA仿真與試驗研究[學位論文]. 南昌: 南昌航空大學, 2014 [9] Mehl J B, Moldover M R, Pitre L. Designing quasi-spherical resonators for acoustic thermometry. Metrologia, 2004, 41(4): 295 doi: 10.1088/0026-1394/41/4/011 [10] Madonna Ripa D, Imbraguglio D, Gaiser C, et al. Refractive index gas thermometry between 13.8 K and 161.4 K. Metrologia, 2021, 58(2): 025008 doi: 10.1088/1681-7575/abe249 [11] Gaiser C, Fellmuth B. Method for extrapolating the compressibility data of solids from room to lower temperatures. Phys Status Solidi B, 2016, 253(8): 1549 doi: 10.1002/pssb.201552717 [12] Mendes S S, Filho J C A D, Melo A R A, et al. Determination of thermal expansion coefficient of a monofilament polyamide fiber using digital image correlation. Polym Test, 2020, 87: 106540 doi: 10.1016/j.polymertesting.2020.106540 [13] James J D, Spittle J A, Brown S R, et al. A review of measurement techniques for the thermal expansion coefficient of metals and alloys at elevated temperatures. Meas Sci Technol, 2001, 12(3): R1 doi: 10.1088/0957-0233/12/3/201 [14] Cooper R F. The thermal expansion of solids. Phys Educ, 1976, 11(4): 284 doi: 10.1016/S0031-8914(58)80103-2 [15] Ventura G, Bianchini G, Gottardi E, et al. Thermal expansion and thermal conductivity of Torlon at low temperatures. Cryogenics, 1999, 39(5): 481 doi: 10.1016/S0011-2275(99)00051-X [16] Roth P, Gmelin E. A capacitance displacement sensor with elastic diaphragm. Rev Sci Instrum, 1992, 63(3): 2051 doi: 10.1063/1.1143165 [17] Hamilton W O, Greene D B, Davidson D E. Thermal expansion of epoxies between 2 and 300°K. Rev Sci Instrum, 1968, 39(5): 645 doi: 10.1063/1.1683465 [18] Smith M H. Technical literature digest. AIAA J, 1963, 1(8): 1971 [19] Keyston J R G, MacPherson J D, Guptill E W. Coefficient of thermal expansion of Barium titanate. Rev Sci Instrum, 1959, 30(4): 246 doi: 10.1063/1.1716527 [20] Pudalov V M, Khaikin M S. Dilatometer with a sensitivity of 10?4 angstrom. Cryogenics, 1969, 9(2): 128 doi: 10.1016/0011-2275(69)90194-5 [21] Ewing M B, Mehl J B, Moldover M R, et al. Microwave measurements of the thermal expansion of a spherical cavity. Metrologia, 1988, 25(4): 211 doi: 10.1088/0026-1394/25/4/003 [22] Moldover M R, Waxman M, Greenspan M. Spherical acoustic resonators for temperature and thermophysical property measurements. High Temp-High Press, 1979, 11: 75 doi: 10.1121/1.2019734 [23] Zhang K, Feng X J, Zhang J T, et al. Microwave measurements of the length and thermal expansion of a cylindrical resonator for primary acoustic gas thermometry. Meas Sci Technol, 2017, 28(1): 015006 doi: 10.1088/1361-6501/28/1/015006 [24] Rourke P M C, Hill K D. Progress toward development of low-temperature microwave refractive index gas thermometry at NRC. Int J Thermophys, 2015, 36(2): 205 [25] May E F, Pitre L, Mehl J B, et al. Quasi-spherical cavity resonators for metrology based on the relative dielectric permittivity of gases. Rev Sci Instrum, 2004, 75(10): 3307 [26] Cheng Y H. Copper Electrorefining Workers (Copper Electrorefining Workers, Sulfate Workers). Beijing: Metallurgical Industry Press, 2013程永紅. 銅電解精煉工(銅電解工、硫酸鹽工). 北京: 冶金工業出版社, 2013 [27] Liu W J, Pitre L, Gao B, et al. Microwave method for closure of quasi-spherical resonator // 2018 Conference on Precision Electromagnetic Measurements (CPEM 2018). Paris, 2018: 1 [28] Preston-Thomas H. The international temperature scale of 1990 (ITS-90). Metrologia, 1990, 27(1): 3 doi: 10.1088/0026-1394/27/1/002 [29] Gao B, Zhang H Y, Han D X, et al. Measurement of thermodynamic temperature between 5 K and 24.5 K with single-pressure refractive-index gas thermometry. Metrologia, 2020, 57(6): 065006 [30] Chen Y Y, Zhang H Y, Song Y N, et al. Thermal response characteristics of a SPRIGT primary thermometry system. Cryogenics, 2019, 97: 1 doi: 10.1016/j.cryogenics.2018.10.015 [31] Hu J F, Zhang H Y, Song Y H, et al. Investigation of high-stability temperature control in primary tas thermometry. J Therm Sci, 2022, 21(3): 765 doi: 10.1016/j.scib.2018.05.023 [32] Keysight Technologies. Overview of vector network analyzer [Z/OL]. Keysight Technologies (2021-03-17) [2021-12-03].https://www.keysight.com/cn/zh/assets/7018-01698/technical-overviews/5989-7603.pdf [33] Keithley. Instrument Driver Network [Z/OL]. Engineer Ambitiously (2002) [2021-12-03].https://sine.ni.com/apps/utf8/niid_web_display.model_page?p_model_id=1547 [34] ISOTECH. F900 precision thermometry bridge—operator’s Handbook [Z/OL]. ISOTECH (2020) [2021-12-3]. http://www.isotechna.com/v/vspfiles/product_manuals/asl/F900.pdf [35] Lake Shore Cryotronics, Inc. Cernox®/technical-specifications [Z/OL]. Lake Shore Cryotronics (2021) [2021-12-3].https://www.lakeshore.com/products/categories/specification/temperature-products/cryogenic-temperature-sensors/cernox [36] Hu J F, Zhang H Y, Song Y N, et al. Investigation of high-stability temperature control in primary gas thermometry. J Therm Sci, 2022, 31(3): 765 [37] Sutton G, Underwood R, Pitre L, et al. Acoustic resonator experiments at the triple point of water: First results for the boltzmann constant and remaining challenges. Int J Thermophys, 2010, 31(7): 1310 [38] Underwood R J, Mehl J B, Pitre L, et al. Waveguide effects on quasispherical microwave cavity resonators. Meas Sci Technol, 2010, 21(7): 075103 doi: 10.1088/0957-0233/21/7/075103 [39] Mehl J B. Second-order electromagnetic eigenfrequencies of a triaxial ellipsoid II. Metrologia, 2015, 52(5): S227 doi: 10.1088/0026-1394/52/5/S227 -




 下載:
下載: