赤蘚糖醇/碳納米管復合相變材料熱特性模擬研究

閆曉鑫; 馮妍卉; 邱琳; 張欣欣

doi:10.13374/j.issn2095-9389.2021.09.14.002

赤蘚糖醇/碳納米管復合相變材料熱特性模擬研究

doi: 10.13374/j.issn2095-9389.2021.09.14.002

閆曉鑫¹,
馮妍卉^{1, 2, ,},
邱琳^{1, 2, ,},
張欣欣^{1, 2}

1.
北京科技大學能源與環境工程學院，北京 100083
2.
北京科技大學冶金工業節能減排北京市重點實驗室，北京 100083

基金項目: 國家重點研發計劃資助項目（2018YFA0702300）；國家自然科學基金資助項目（51876007，51876008）；北京市科技新星計劃資助項目（Z201100006820065）；北京市自然科學基金資助項目（3202020）；北京科技大學青年教師學科交叉研究資助項目（中央高校基本科研業務費專項資金）（FRF-IDRY-19-004）

詳細信息

通訊作者:
馮妍卉，E-mail: yhfeng@me.ustb.edu.cn

邱琳，E-mail: qiulin@ustb.edu.cn

中圖分類號: TK02
計量
- 文章訪問數: 4225
- HTML全文瀏覽量: 380
- PDF下載量: 70
- 被引次數: 0
出版歷程
- 收稿日期: 2021-09-14
- 網絡出版日期: 2021-12-02
- 刊出日期: 2022-04-02

Simulation of thermal properties of erythritol/carbon nanotube composite phase change materials

YAN Xiao-xin¹,
FENG Yan-hui^{1, 2
, ,},
QIU Lin^{1, 2
, ,},
ZHANG Xin-xin^{1, 2}

1.
School of Energy and Environmental Engineering, University of Science and Technology Beijing, Beijing 100083, China
2.
Beijing Key Laboratory of Energy Conservation and Emission Reduction in Metallurgical Industry, University of Science and Technology Beijing, Beijing 100083, China

More Information

Corresponding author: FENG Yan-hui, E-mail: yhfeng@me.ustb.edu.cn; QIU Lin, E-mail: qiulin@ustb.edu.cn

摘要

摘要: 在“碳達峰、碳中和”的大背景下，能源結構從一次能源向新能源轉變刻不容緩。由于新能源具有間歇性、波動性的特點，儲能技術可以有效解決上述問題而得到了廣泛的關注。相變材料作為儲能技術的關鍵，其熱導率低的問題亟需解決。赤蘚糖醇作為中低溫區常用的高焓值相變材料，熱導率僅為0.7 W?m^–1?K^–1，嚴重制約了實際應用中的能量利用效率。本文以赤蘚糖醇作為主要研究對象，采用具有超高導熱系數的單壁碳納米管作為導熱增強材料，借助分子動力學模擬的方法探究了碳納米管長度、質量分數以及分布方式對赤蘚糖醇/碳納米管復合相變材料熱導率的影響規律。當碳納米管軸向長度小于其聲子平均自由程時，復合相變材料熱導率隨碳納米管軸向長度增加而增大，同時隨碳納米管質量分數增加而增大，但表現出顯著的各向異性。由于引入赤蘚糖醇–碳納米管界面，復合相變材料徑向熱導率相比純赤蘚糖醇反而降低。當碳納米管在赤蘚糖醇中隨機分布時，熱導率的各向異性得到了顯著改善且各方向熱導率均得到了提升。通過對比復合前后赤蘚糖醇與碳納米管的聲子振動態密度發現，由于兩者間的相互作用，碳納米管的聲子振動受到抑制，而赤蘚糖醇中聲子熱輸運得到激發，從而提高了熱導率。
- 赤蘚糖醇 /
- 碳納米管 /
- 復合相變材料 /
- 熱導率 /
- 分子動力學模擬
Abstract: In the area of “carbon peaking and carbon neutralization,” changing energy structure from primary energy to new energy is an extremely important issue. Due to the intermittent and fluctuating characteristics of new energy, energy storage technology has proven a viable solution to this issue thus has attracted extensive attention. As a key to energy storage technology, the problem of the low thermal conductivity of phase change materials (PCMs) requires immediate attention. Erythritol is a high enthalpy phase change material commonly used in low-to-medium temperature processes. Its thermal conductivity of only 0.7 W?m^–1?K^–1 seriously hinders its energy utilization efficiency in practical application. In this paper, erythritol is the main research focus, and single-walled carbon nanotubes (CNTs) of ultra-high thermal conductivity are used as thermal conductivity reinforcements. The effects of length, mass fraction, and the distribution of CNTs on the thermal conductivity of erythritol/CNT composite PCMs were studied by means of molecular dynamics simulation. When the axial lengths of the CNTs were less than their phonon mean free paths, the thermal conductivity of the composite PCMs increased with increasing CNT axial length and mass fraction, although clear anisotropy was exhibited. Due to the introduction of erythritol–CNTs interfacial thermal resistance, the radial thermal conductivity of the composite materials was lower than that of pure erythritol. When CNTs were randomly distributed in erythritol, the anisotropy of thermal conductivity was significantly improved, as was thermal conductivity in all directions. Comparing the phonon vibration densities of the states of erythritol and CNT before and after recombination, it was found that, due to the interaction between the two, the phonon vibration of CNT was suppressed, and the phonon heat transport in erythritol was excited, thus improving thermal conductivity.
- erythritol /
- carbon nanotubes /
- composite phase change materials /
- thermal conductivity /
- molecular dynamic simulation

HTML全文

圖 1 赤蘚糖醇/碳納米管復合結構模型圖。（a）赤蘚糖醇單晶胞結構；（b）碳納米管質量分數分別為8.88%和13.35%的赤蘚糖醇/碳納米管復合結構模型

Figure 1. Erythritol/carbon nanotube composite structure model: (a) erythritol single cell structure; (b) erythritol/carbon nanotube composite structure model with a carbon nanotube mass fraction of 8.88% and 13.35%

下載: 全尺寸圖片幻燈片

圖 2 NEMD方法計算熱導率示意圖

Figure 2. Schematic model of the NEMD method for thermal conductivity calculation

下載: 全尺寸圖片幻燈片

圖 3 293 K溫度下赤蘚糖醇密度隨馳豫時間變化

Figure 3. Density of erythritol changes with a relaxation time at 293 K

下載: 全尺寸圖片幻燈片

圖 4 NEMD方法熱流與溫度分布圖。（a）體系施加/提取的能量（斜率為熱流）；（b）體系溫度分布圖

Figure 4. Heat flow and temperature distribution diagram of the NEMD method: (a) energy added/subtracted by the system (the slope is heat flux); (b) temperature distribution of the system

下載: 全尺寸圖片幻燈片

圖 5 赤蘚糖醇/碳納米管復合材料熱導率隨碳納米管長度變化

Figure 5. Thermal conductivity of erythritol/CNT composites as a function of the length of CNT

下載: 全尺寸圖片幻燈片

圖 6 （a）赤蘚糖醇/碳納米管復合材料熱導率隨碳納米管質量分數變化；（b）赤蘚糖醇與碳納米管間相互作用能隨碳納米管質量分數變化

Figure 6. (a) Thermal conductivity of erythritol/CNT composites as a function of the mass fraction of CNT; (b) interaction energy between erythritol and CNT varies with the mass fraction of CNT

下載: 全尺寸圖片幻燈片

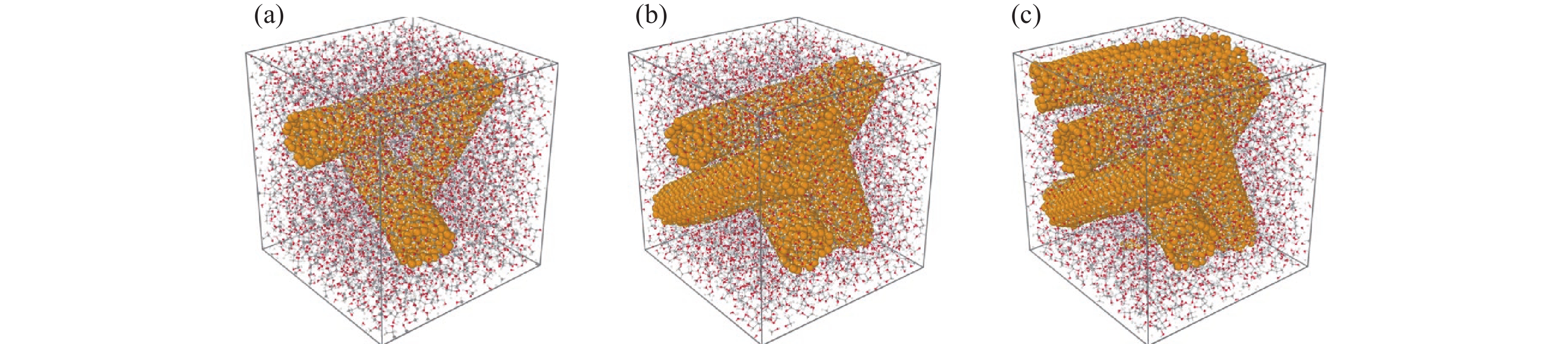
圖 7 赤蘚糖醇/碳納米管隨機填充復合模型。（a）赤蘚糖醇/碳納米管（3根）復合材料隨機模型；（b）赤蘚糖醇/碳納米管（5根）復合材料隨機模型；（c）赤蘚糖醇/碳納米管（6根）復合材料隨機模型

Figure 7. Random filling model of erythritol/CNTs: (a) random filling model of erythritol/3 CNTs composites; (b) random filling model of erythritol/5 CNTs composites; (c) random filling model of erythritol/6 CNTs composites

下載: 全尺寸圖片幻燈片

圖 8 赤蘚糖醇/碳納米管復合材料聲子振動態密度。（a）碳納米管復合前后聲子振動態密度；（b）赤蘚糖醇復合前后聲子振動態密度

Figure 8. VDOS of erythritol/CNT composite: (a) VDOS of CNTs before and after compound; (b) VDOS of erythritol before and after compound

下載: 全尺寸圖片幻燈片

表 1 赤蘚糖醇與碳納米管不同種類原子間L-J勢參數

Table 1. L-J potential parameters between erythritol and different kinds of carbon nanotubes

Atom type	ε_ij / eV	σ_ij / nm
C₂-C_p	0.0028	0.3000
C₁-C_p	0.0028	0.3000
Oh-C_p	0.0033	0.3620
ho-C_p	0.0021	0.3025
h-C_p	0.0000	0.0000

下載: 導出CSV

表 2 隨機分布方式下赤蘚糖醇/碳納米管復合材料熱導率

Table 2. Thermal conductivity of erythritol/CNTs composites with random distribution

Number of CNTs	k_x / (W?m^–1?K^–1)	k_y / (W?m^–1?K^–1)	k_z / (W?m^–1?K^–1)	k_mean / (W?m^–1?K^–1)	Enhancement ratio / %
3 (mass fraction of 16.00%)	1.61±0.03	1.61±0.07	1.29±0.03	1.50±0.01	123.88
5 (mass fraction of 25.28%)	2.28±0.01	1.61±0.01	1.92±0.06	1.94±0.02	189.56
6 (mass fraction of 30.33%)	2.27±0.11	2.33±0.10	1.87±0.08	2.16±0.06	222.39

下載: 導出CSV

www.77susu.com

參考文獻(40)

[1]	Iijima S. Helical microtubules of graphitic carbon. Nature, 1991, 354(6348): 56 doi: 10.1038/354056a0
[2]	Qiu L, Zhu N, Feng Y H, et al. A review of recent advances in thermophysical properties at the nanoscale: From solid state to colloids. Phys Rep, 2020, 843: 1 doi: 10.1016/j.physrep.2019.12.001
[3]	Hone J, Whitney M, Piskoti C, et al. Thermal conductivity of single-walled carbon nanotubes. Phys Rev B, 1999, 59(4): R2514 doi: 10.1103/PhysRevB.59.R2514
[4]	Berber S, Kwon Y K, Tománek D. Unusually high thermal conductivity of carbon nanotubes. Phys Rev Lett, 2000, 84(20): 4613 doi: 10.1103/PhysRevLett.84.4613
[5]	Xu C, Xu S L, Eticha R D. Experimental investigation of thermal performance for pulsating flow in a microchannel heat sink filled with PCM (paraffin/CNT composite). Energy Convers Manag, 2021, 236: 114071 doi: 10.1016/j.enconman.2021.114071
[6]	Al-Ahmed A, Sar? A, Mazumder M A J, et al. Thermal energy storage and thermal conductivity properties of fatty acid/fatty acid-grafted-CNTs and fatty acid/CNTs as novel composite phase change materials. Sci Rep, 2020, 10: 15388 doi: 10.1038/s41598-020-71891-1
[7]	Cong R S, Xu C L, Chen Y K, et al. Enhanced thermal conductivity of palmitic acid/copper foam composites with carbon nanotube as thermal energy storage materials. J Energy Storage, 2021, 40: 102783 doi: 10.1016/j.est.2021.102783
[8]	Rabady R I, Malkawi D S. Thermal conductivity enhancement of sodium thiosulfate pentahydrate by adding carbon nano-tubes/graphite nano-particles. J Energy Storage, 2020, 27: 101166 doi: 10.1016/j.est.2019.101166
[9]	Li A, Hai G T, Cheng P, et al. Molecular insights into the interaction mechanism between C18 phase change materials and methyl-modified carbon nanotubes. Ceram Int, 2021, 47(16): 23564 doi: 10.1016/j.ceramint.2021.05.074
[10]	Tafrishi H, Sadeghzadeh S, Ahmadi R, et al. Investigation of tetracosane thermal transport in presence of graphene and carbon nanotube fillers—A molecular dynamics study. J Energy Storage, 2020, 29: 101321 doi: 10.1016/j.est.2020.101321
[11]	Yu Y S, Zhao C Y, Tao Y B, et al. Superior thermal energy storage performance of NaCl–SWCNT composite phase change materials: A molecular dynamics approach. Appl Energy, 2021, 290: 116799 doi: 10.1016/j.apenergy.2021.116799
[12]	Du Y P, Zhou T, Zhao C Y, et al. Molecular dynamics simulation on thermal enhancement for carbon nano tubes (CNTs) based phase change materials (PCMs). Int J Heat Mass Transf, 2022, 182: 122017 doi: 10.1016/j.ijheatmasstransfer.2021.122017
[13]	Zhang H C, Rindt C C M, Smeulders D M J, et al. Nanoscale heat transfer in carbon nanotubes - sugar alcohol composite as heat storage materials. J Phys Chem C, 2016, 120(38): 21915 doi: 10.1021/acs.jpcc.6b05466
[14]	Zou H Y, Feng Y H, Qiu L, et al. Effect of the loading amount and arrangement of iodine chains on the interfacial thermal transport of carbon nanotubes: A molecular dynamics study. RSC Adv, 2020, 10(72): 44196 doi: 10.1039/D0RA06870E
[15]	Ikeshoji T, Hafskjold B. Non-equilibrium molecular dynamics calculation of heat conduction in liquid and through liquid-gas interface. Mol Phys, 1994, 81(2): 251 doi: 10.1080/00268979400100171
[16]	Jund P, Jullien R. Molecular-dynamics calculation of the thermal conductivity of vitreous silica. Phys Rev B, 1999, 59(21): 13707 doi: 10.1103/PhysRevB.59.13707
[17]	Müller-Plathe F. A simple nonequilibrium molecular dynamics method for calculating the thermal conductivity. J Chem Phys, 1997, 106(14): 6082 doi: 10.1063/1.473271
[18]	Zhang Q, Luo Z L, Guo Q L, et al. Preparation and thermal properties of short carbon fibers/erythritol phase change materials. Energy Convers Manag, 2017, 136: 220 doi: 10.1016/j.enconman.2017.01.023
[19]	Shimada A. Crystal and molecular structure of mesoerythritol. Acta Cryst, 1958, 11(10): 748 doi: 10.1107/S0365110X58002036
[20]	Plimpton S. Fast parallel algorithms for short-range molecular dynamics. J Comput Phys, 1995, 117(1): 1 doi: 10.1006/jcph.1995.1039
[21]	Stukowski A. Visualization and analysis of atomistic simulation data with OVITO–the open visualization tool. Modelling Simul Mater Sci Eng, 2010, 18(1): 015012 doi: 10.1088/0965-0393/18/1/015012
[22]	Schmid N, Eichenberger A P, Choutko A, et al. Definition and testing of the GROMOS force-field versions 54A7 and 54B7. Eur Biophys J, 2011, 40(7): 843 doi: 10.1007/s00249-011-0700-9
[23]	Tersoff J. New empirical approach for the structure and energy of covalent systems. Phys Rev B, 1988, 37(12): 6991 doi: 10.1103/PhysRevB.37.6991
[24]	Qiu L, Zhu N, Feng Y H, et al. Interfacial thermal transport properties of polyurethane/carbon nanotube hybrid composites. Int J Heat Mass Transf, 2020, 152: 119565 doi: 10.1016/j.ijheatmasstransfer.2020.119565
[25]	Hu Y, Feng T L, Gu X K, et al. Unification of nonequilibrium molecular dynamics and the mode-resolved phonon Boltzmann equation for thermal transport simulations. Phys Rev B, 2020, 101(15): 155308 doi: 10.1103/PhysRevB.101.155308
[26]	Li Z, Xiong S Y, Sievers C, et al. Influence of thermostatting on nonequilibrium molecular dynamics simulations of heat conduction in solids. J Chem Phys, 2019, 151(23): 234105 doi: 10.1063/1.5132543
[27]	Feng B, Fan L W, Zeng Y, et al. Atomistic insights into the effects of hydrogen bonds on the melting process and heat conduction of erythritol as a promising latent heat storage material. Int J Therm Sci, 2019, 146: 106103 doi: 10.1016/j.ijthermalsci.2019.106103
[28]	Yan X X, Feng Y H, Qiu L, et al. Thermal conductivity and phase change characteristics of hierarchical porous diamond/erythritol composite phase change materials. Energy, 2021, 233: 121158 doi: 10.1016/j.energy.2021.121158
[29]	H?hlein S, K?nig-Haagen A, Brüggemann D. Thermophysical characterization of MgCl₂·6H₂O, xylitol and erythritol as phase change materials (PCM) for latent heat thermal energy storage (LHTES). Materials, 2017, 10(4): 444 doi: 10.3390/ma10040444
[30]	Chai Y, Xiao Z Y, Chan P C H. Horizontally aligned carbon nanotube bundles for interconnect application: Diameter-dependent contact resistance and mean free path. Nanotechnology, 2010, 21(23): 235705 doi: 10.1088/0957-4484/21/23/235705
[31]	Yu C, Shi L, Yao Z, et al. Thermal conductance and thermopower of an individual single-wall carbon nanotube. Nano Lett, 2005, 5(9): 1842 doi: 10.1021/nl051044e
[32]	S??skilahti K, Oksanen J, Volz S, et al. Frequency-dependent phonon mean free path in carbon nanotubes from nonequilibrium molecular dynamics. Phys Rev B, 2015, 91(11): 115426 doi: 10.1103/PhysRevB.91.115426
[33]	Wang J, Li C, Li J, et al. A multiscale study of the filler-size and temperature dependence of the thermal conductivity of graphene-polymer nanocomposites. Carbon, 2021, 175: 259 doi: 10.1016/j.carbon.2020.12.086
[34]	Bae M H, Li Z Y, Aksamija Z, et al. Ballistic to diffusive crossover of heat flow in graphene ribbons. Nat Commun, 2013, 4: 1734 doi: 10.1038/ncomms2755
[35]	Qiu L, Zhang X H, Guo Z X, et al. Interfacial heat transport in nano-carbon assemblies. Carbon, 2021, 178: 391 doi: 10.1016/j.carbon.2021.02.105
[36]	Feng D L, Feng Y H, Liu Y Z, et al. Thermal conductivity of a 2D covalent organic framework and its enhancement using fullerene 3D self-assembly: A molecular dynamics simulation. J Phys Chem C, 2020, 124(15): 8386 doi: 10.1021/acs.jpcc.0c00448
[37]	Yousefi F, Khoeini F, Rajabpour A. Thermal conductivity and thermal rectification of nanoporous graphene: A molecular dynamics simulation. Int J Heat Mass Transf, 2020, 146: 118884 doi: 10.1016/j.ijheatmasstransfer.2019.118884
[38]	Yu Z P, Feng Y H, Feng D L, et al. Thermal conductance bottleneck of a three dimensional graphene–CNT hybrid structure: A molecular dynamics simulation. Phys Chem Chem Phys, 2019, 22(1): 337
[39]	Zhao C Y, Tao Y B, Yu Y S. Molecular dynamics simulation of thermal and phonon transport characteristics of nanocomposite phase change material. J Mol Liq, 2021, 329: 115448 doi: 10.1016/j.molliq.2021.115448
[40]	Dickey J M, Paskin A. Computer simulation of the lattice dynamics of solids. Phys Rev, 1969, 188(3): 1407 doi: 10.1103/PhysRev.188.1407