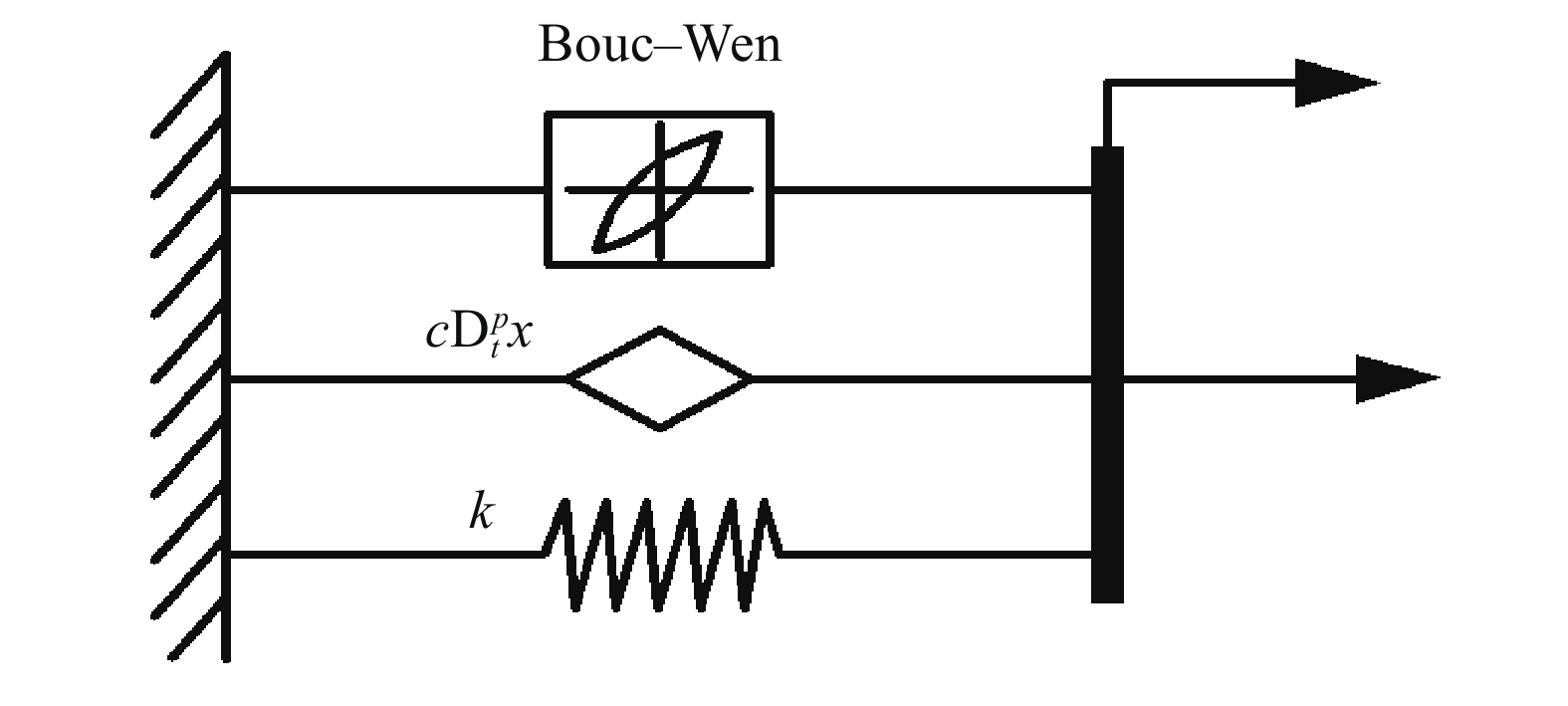
Modified Bouc?Wen model based on a fractional derivative for describing the hysteretic characteristics of magnetorheological elastomers
-
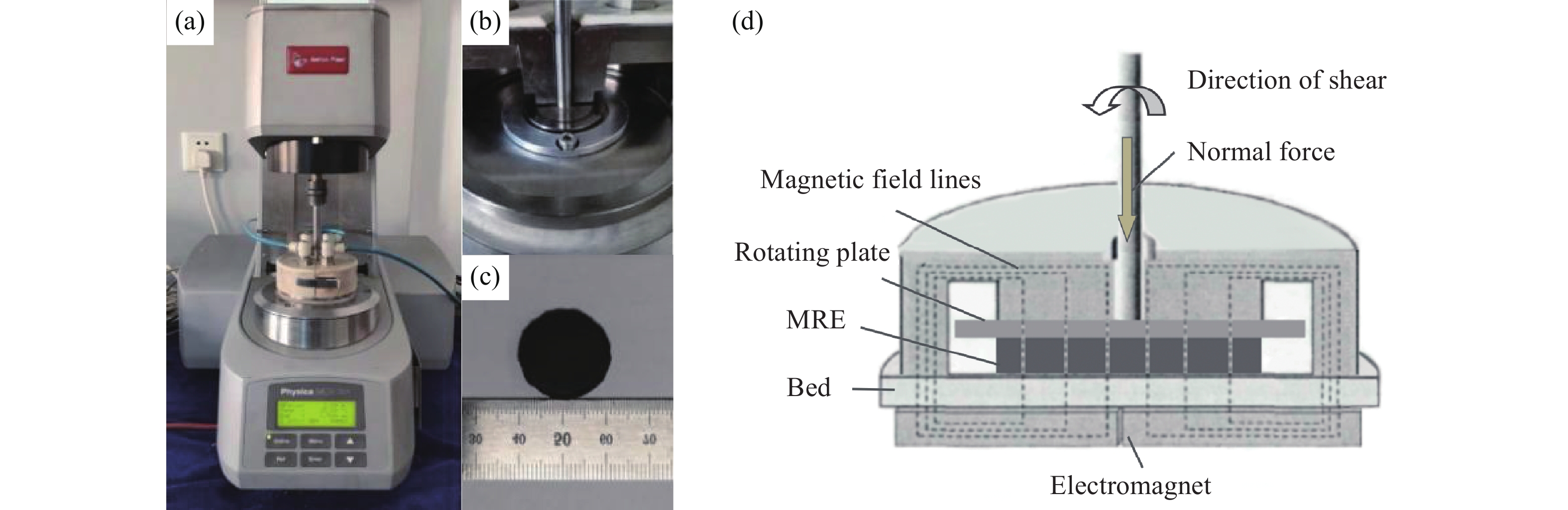
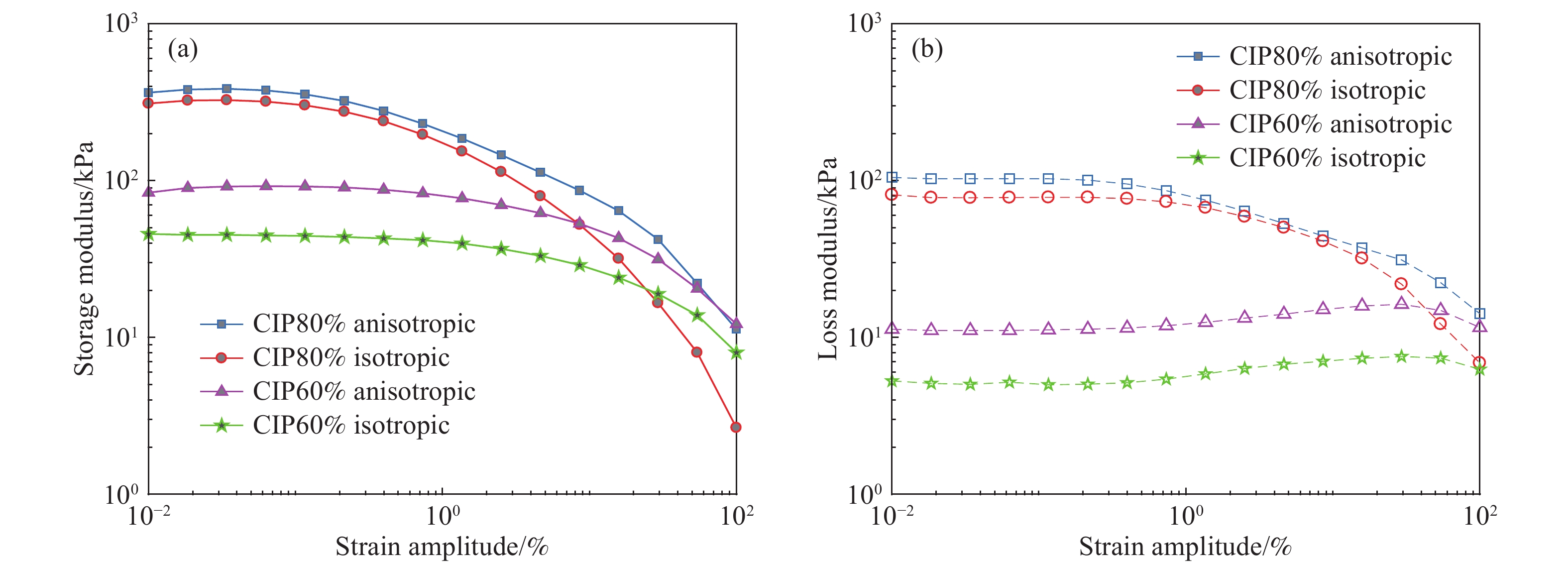
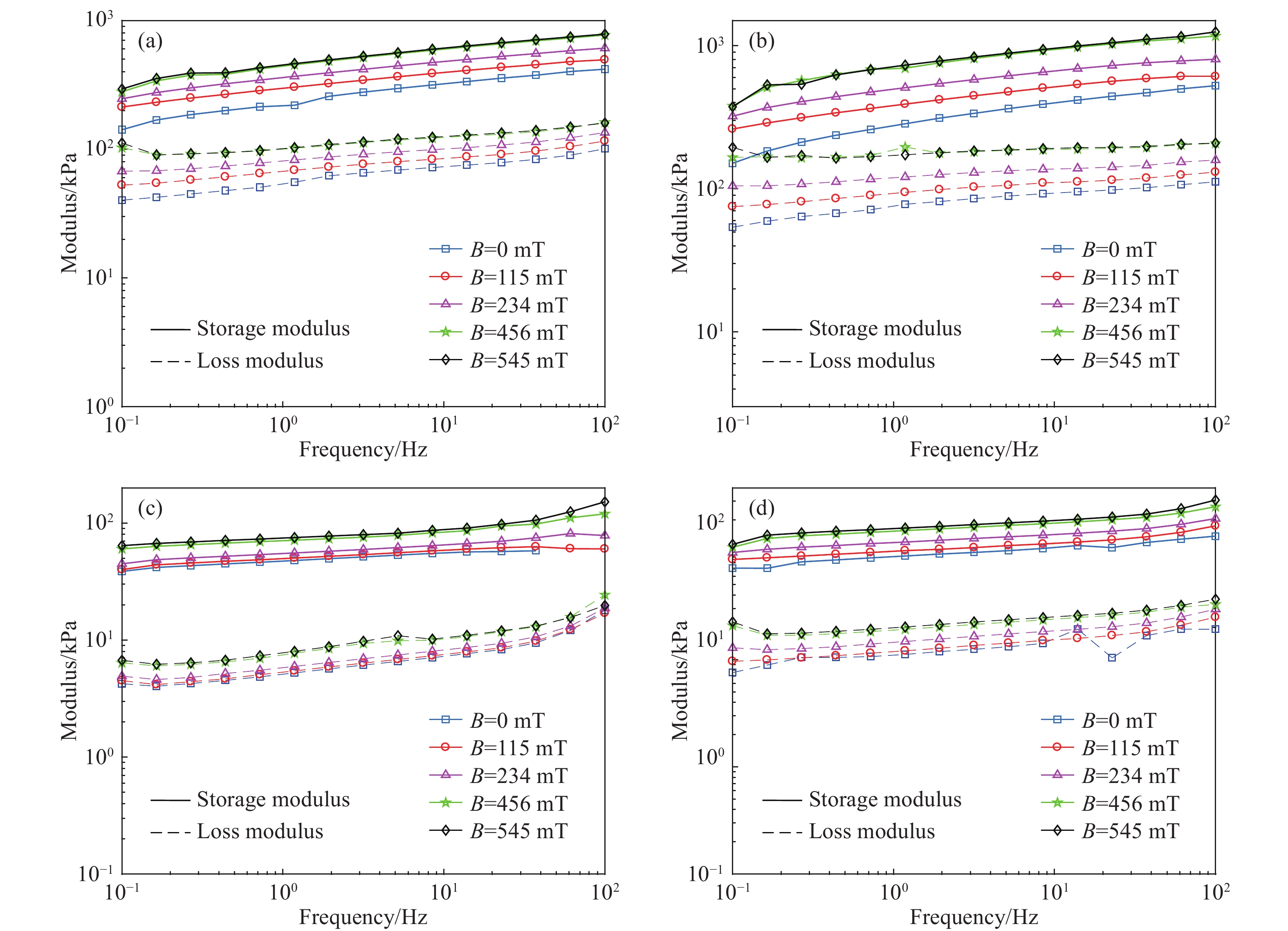
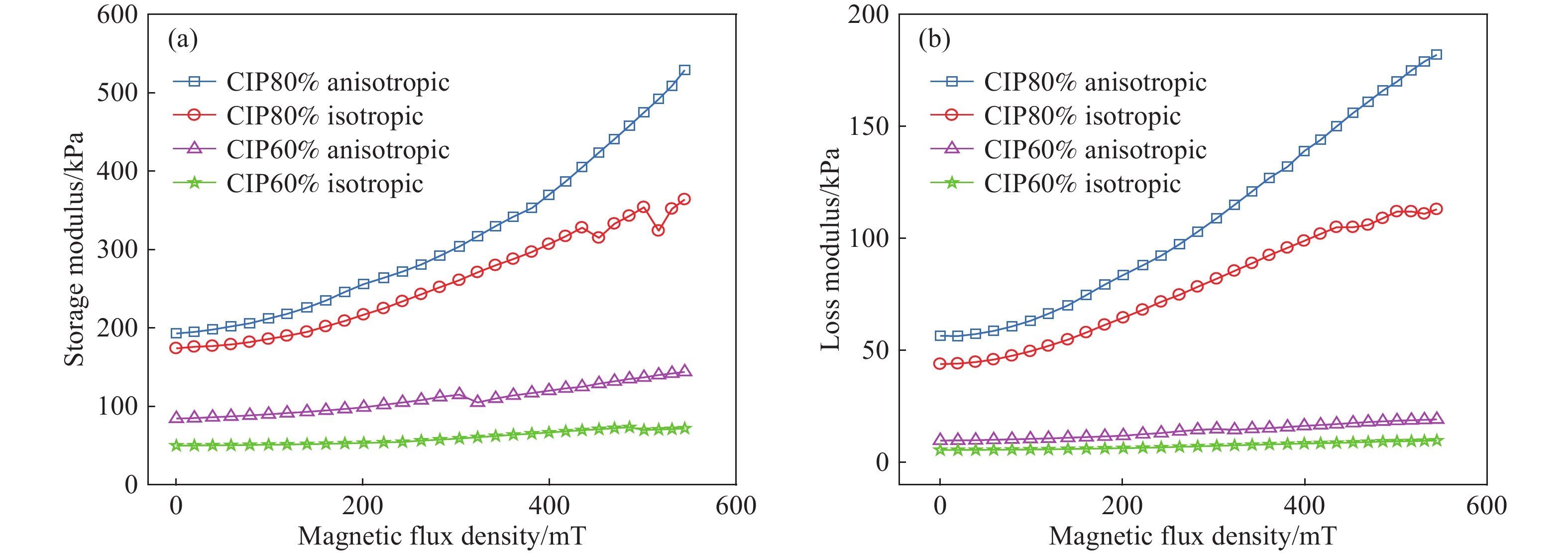
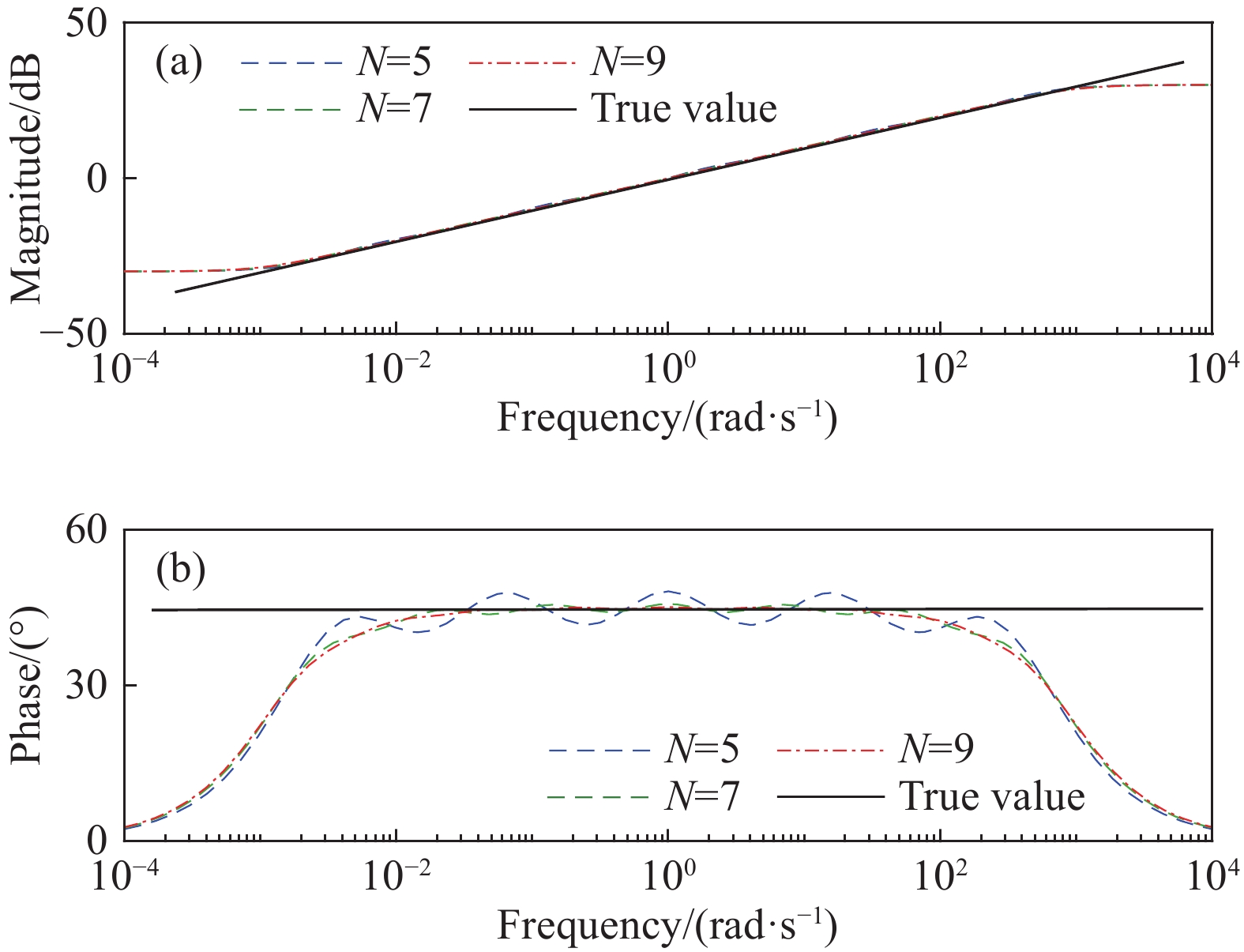
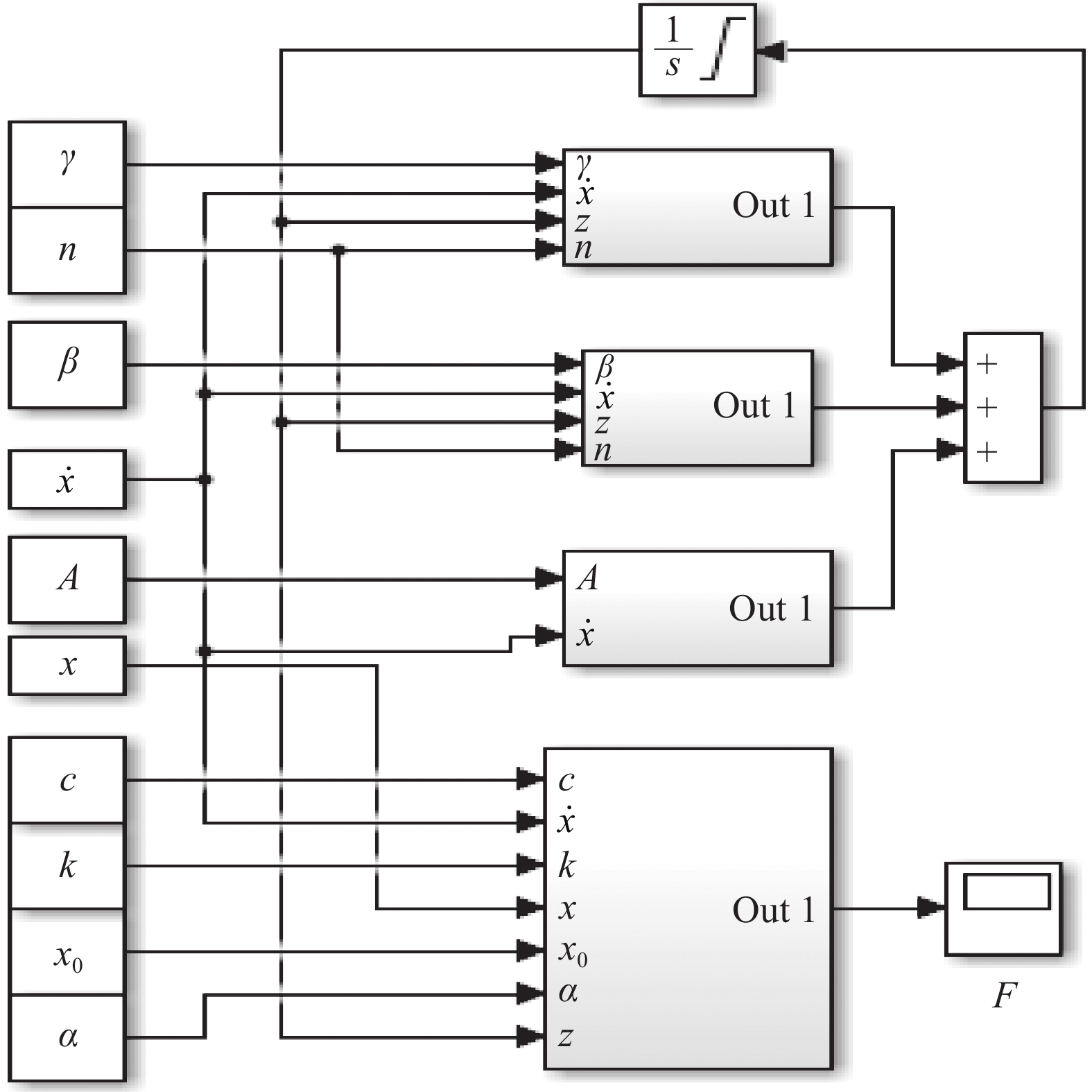
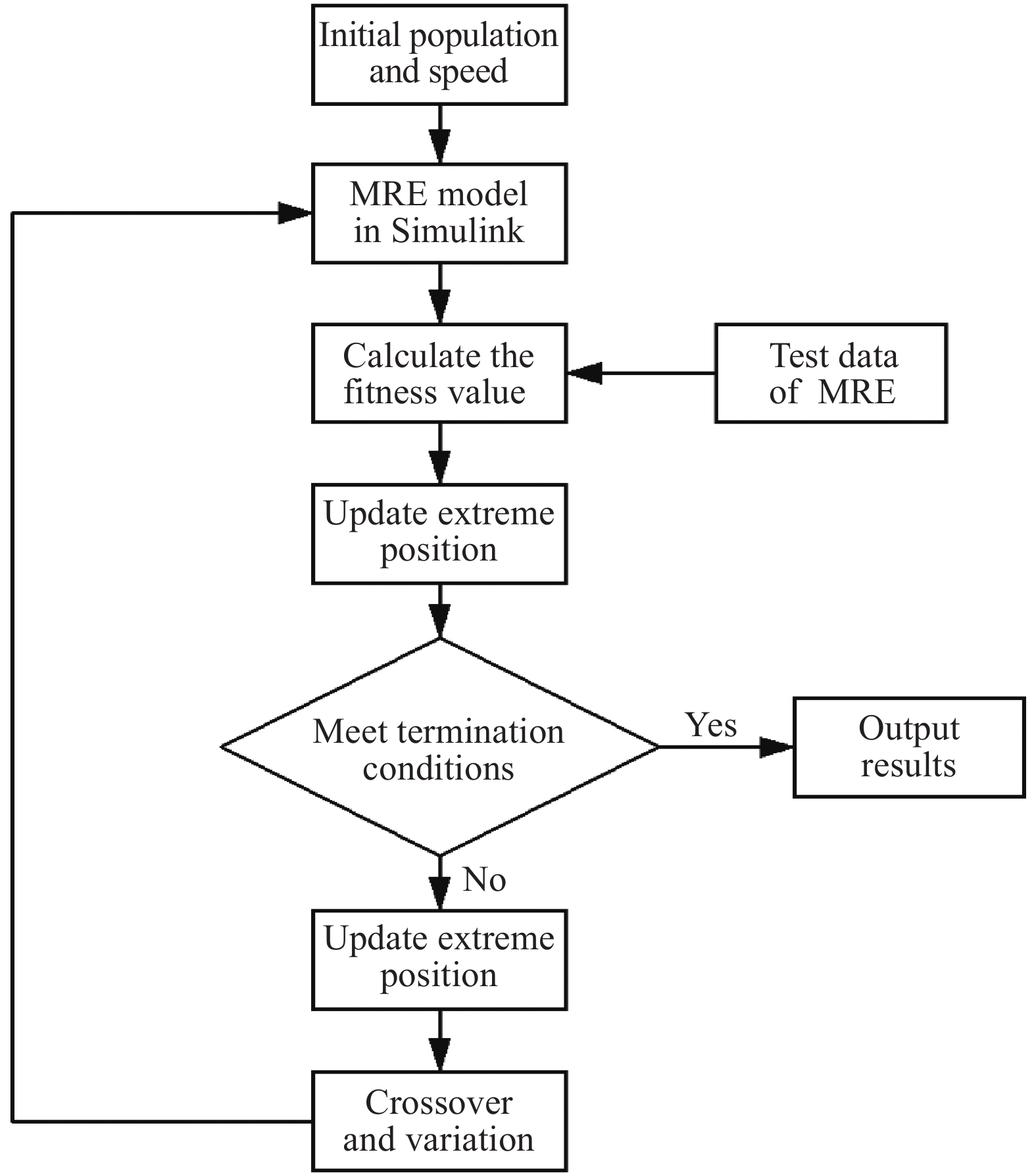
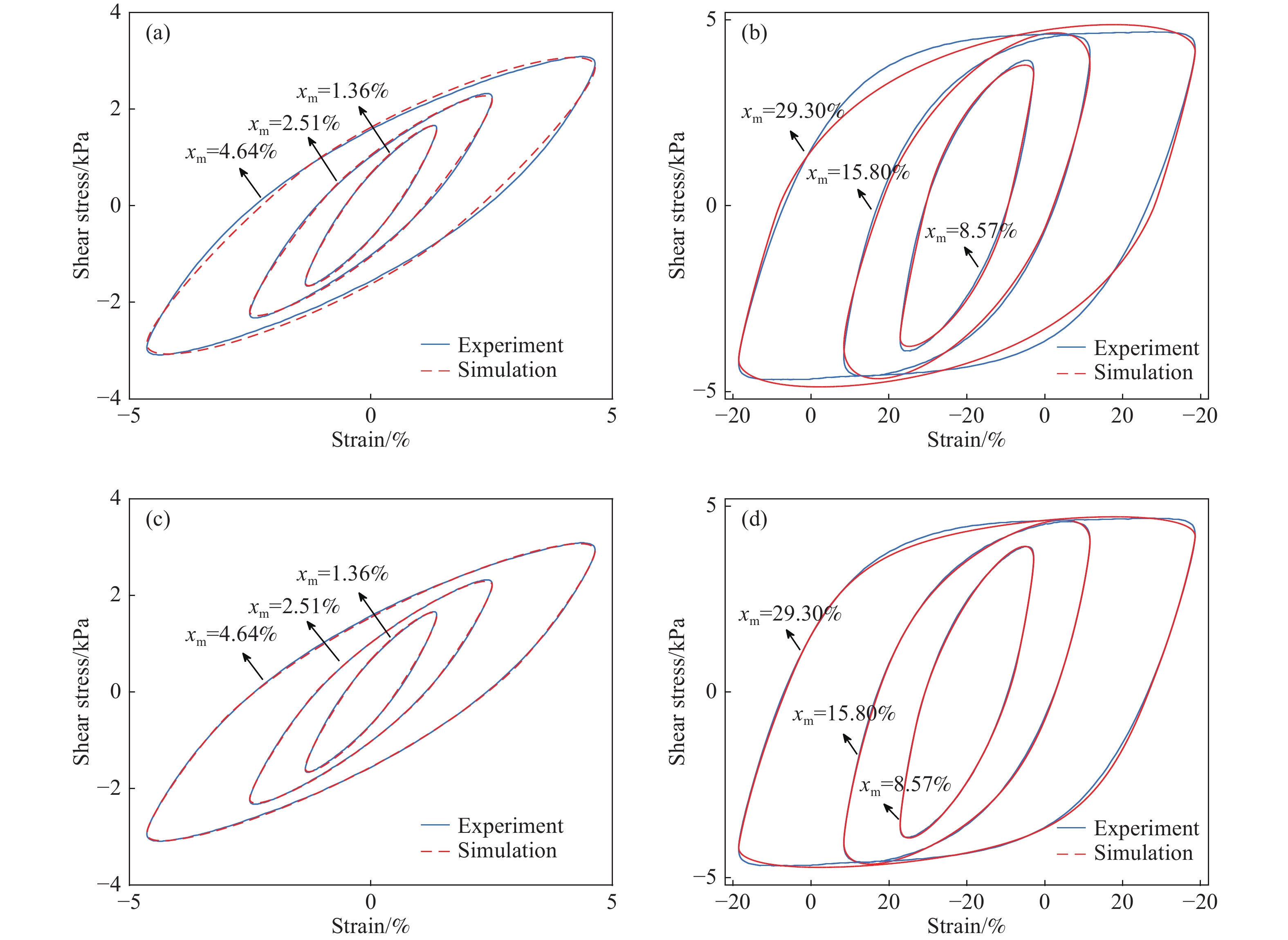
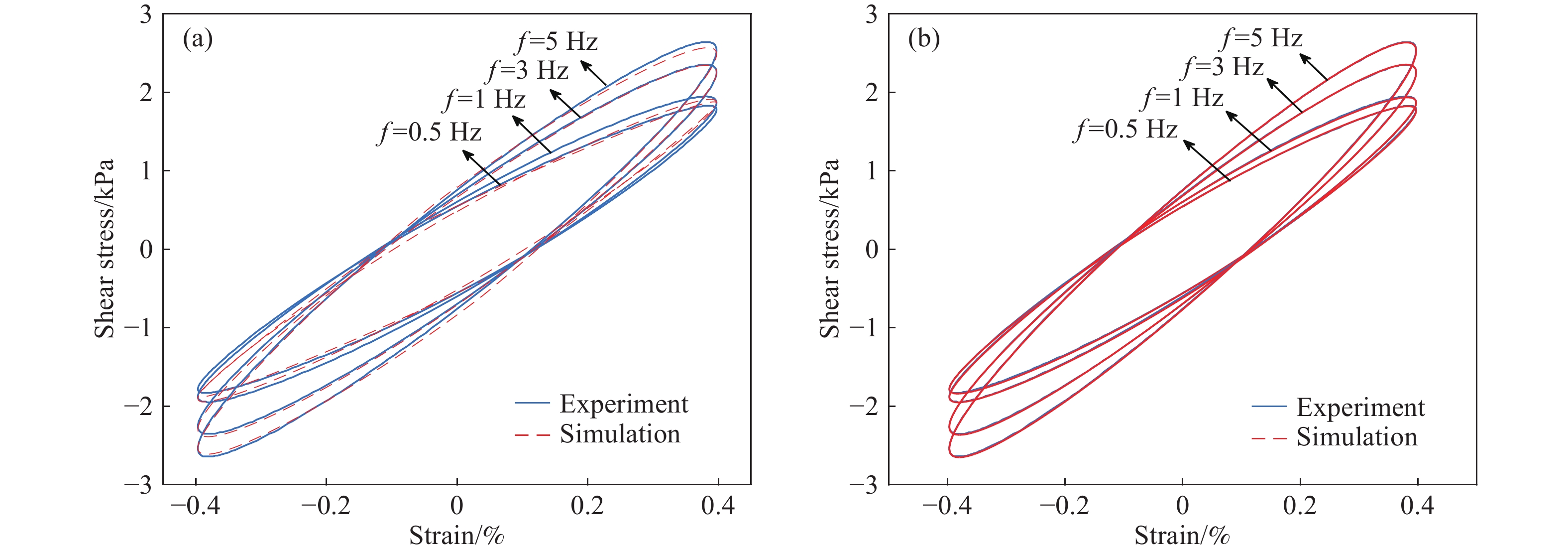
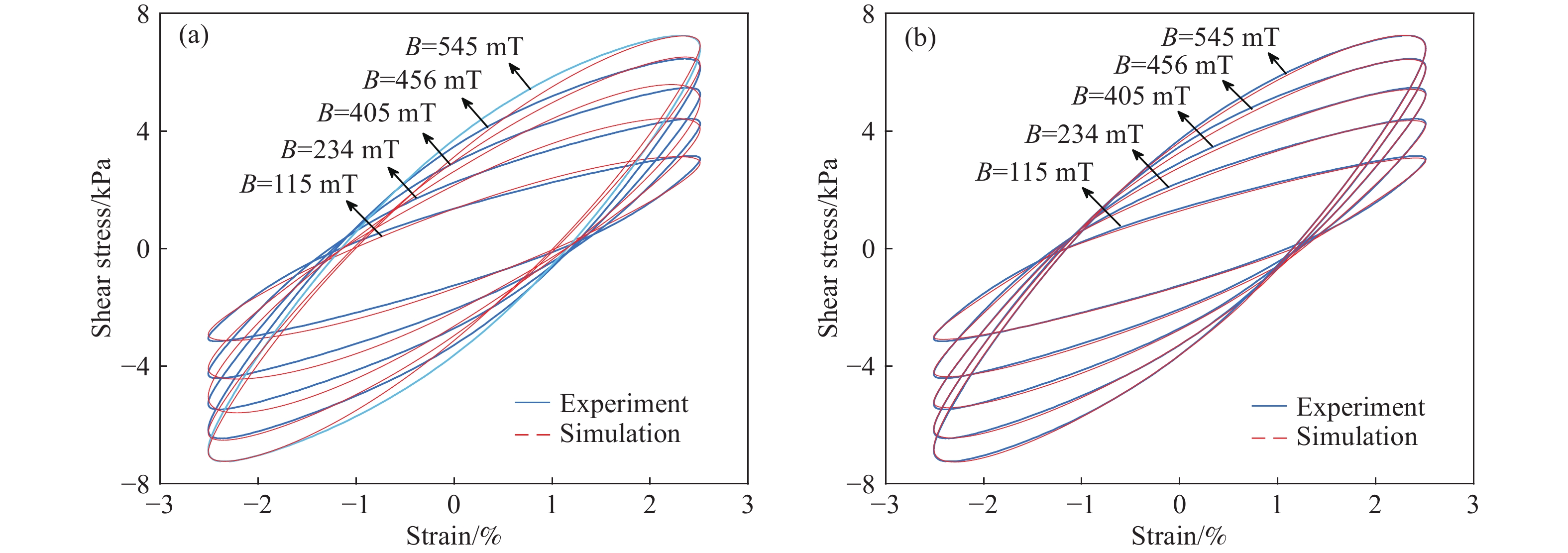
摘要: 為了準確表征大范圍應變幅值、激勵頻率和磁場下磁流變彈性體(Magnetorheological elastomer, MRE)的力學行為，本文引入黏彈性分數階導數，提出一種描述磁流變彈性體滯回特性的分數階導數改進Bouc?Wen模型。分析了各向同性與異性MRE的微觀形貌特征，對MRE進行了性能試驗，研究發現，MRE的儲能和損耗模量隨著應變幅值(0～100%)增大先不變后減小，隨著頻率(0～100 Hz)增大而增大，隨著磁場(0～545 mT)增大而增大。在此基礎上，基于分數階導數提出改進Bouc?Wen模型，在Simulink軟件中建立仿真模型，利用Oustaloup濾波器算法對分數階導數項近似計算，對比分析驗證了改進模型的有效性，各工況下仿真數據和試驗數據的吻合度均高于98%。結果表明：改進Bouc?Wen模型能準確地模擬MRE應力應變滯回曲線，擬合精度較Bouc?Wen模型明顯提升，改進模型在較寬的應變幅值、頻率和磁場范圍內是準確有效的，為實現MRE的工程應用打下基礎。Abstract: As a new type of magnetic sensitivity smart material, magnetorheological elastomers showing a good magnetorheological effect have been broadly applied in the field of intelligent structures and devices. A viscoelastic fractional derivative element was introduced into the stress?strain relationship of magnetorheological elastomers based on the Bouc?Wen model to accurately characterize the mechanical behavior of magnetorheological elastomers under a wide range of strain amplitude, excitation frequency, and magnetic field and to make it better applied in engineering practice. Further, a modified Bouc?Wen model based on a fractional derivative was proposed to describe the hysteresis characteristics of magnetorheological elastomers. The Bouc?Wen model has good universality and can accurately describe the hysteretic characteristics of the magnetorheological elastomer’s nonlinear viscoelastic region, but it cannot accurately simulate magneto-viscoelasticity and frequency dependence. The fractional derivative can express this characteristic with fewer parameters and higher accuracy. The micromorphology characteristics of isotropic and anisotropic magnetorheological elastomers were analyzed, and the performance tests of the magnetorheological elastomers were conducted. The storage and loss modulus of the magnetorheological elastomers initially remain unchanged and then decrease with an increase in strain amplitude (0–100%). Moreover, the storage and loss modulus of the magnetorheological elastomers increase with an increase in frequency (0–100 Hz) and magnetic flux density (0–545 mT). On this basis, a modified Bouc?Wen model was proposed based on the fractional derivative. The simulation model was established using the Simulink software, and the fractional derivative part of the modified model was approximately calculated using the Oustaloup filter algorithm. The effectiveness of the modified model was verified through a comparative analysis. The fitness values of simulation and experimental data under different loading conditions are higher than 98%. Results show that the modified Bouc?Wen model can accurately simulate the stress?strain hysteresis loops of the magnetorheological elastomers, and the fitting accuracy is significantly improved compared with that of the Bouc?Wen model. The modified model is accurate and effective in a wide range of strain amplitudes, frequencies, and magnetic fields, which can lay a foundation for the engineering application of magnetorheological elastomers.
-
圖 2 MRE的截面形貌。（a）CIP60%各向同性；（b）CIP80%各向同性；（c）CIP60%各向異性；（d）CIP80%各向異性
Figure 2. Cross section of MRE: (a) CIP60% isotropic; (b) CIP80% isotropic; (c) CIP60% anisotropic; (d) CIP80% anisotropy
圖 3 （a，b）旋轉流變儀；（c）MRE試件；（d）測試示意圖
Figure 3. (a, b) Rotary rheometer; (c) MRE specimen; (d) schematic of the measuring system
圖 4 MRE的儲能和損耗模量隨應變幅值的變化曲線。（a）儲能模量；（b）損耗模量
Figure 4. Storage modulus (a) and loss modulus (b) curves of MRE with strain amplitude
圖 5 MRE的儲能和損耗模量隨應變頻率的變化曲線。（a）CIP80%各向同性；（b）CIP80%各向異性；（c）CIP60%各向同性；（d）CIP60%各向異性
Figure 5. Storage and loss modulus curves of MRE with strain frequency: (a) CIP80% isotropic; (b) CIP80% anisotropic; (c) CIP60% isotropic; (d) CIP60% anisotropic
圖 6 MRE儲能和損耗模量隨磁感應強度的變化曲線。（a）儲能模量；（b）損耗模量
Figure 6. Storage modulus (a) and loss modulus (b) of MRE with magnetic flux density
圖 8 頻率響應曲線。（a）幅頻；（b）相頻
Figure 8. Frequency response curves: (a) amplitude-frequency; (b) phase-frequency
圖 11 不同幅值下的仿真與試驗數據對比。（a, b）Bouc?Wen模型；（c, d） 改進Bouc?Wen模型
Figure 11. Comparison of simulation and experimental data under different amplitudes: (a, b) Bouc?Wen model; (c, d) modified Bouc?Wen model
圖 12 不同頻率下的仿真與試驗數據對比。（a）Bouc?Wen模型；（b）改進Bouc?Wen模型
Figure 12. Comparison of simulation and test data under different frequencies: (a) Bouc?Wen model; (b) modified Bouc?Wen model
圖 13 不同磁場下的仿真與試驗數據對比。（a）Bouc?Wen模型；（b）改進Bouc?Wen模型
Figure 13. Comparison of simulation and test data under different magnetic flux densities: (a) Bouc?Wen model; (b) modified Bouc?Wen model
圖 14 各參數的變化趨勢。（a～h）不同應變幅值下；（i～p）不同磁感應強度下
Figure 14. Change trends of parameters under different strain amplitudes (a?h) and under different magnetic flux densities (i?p)
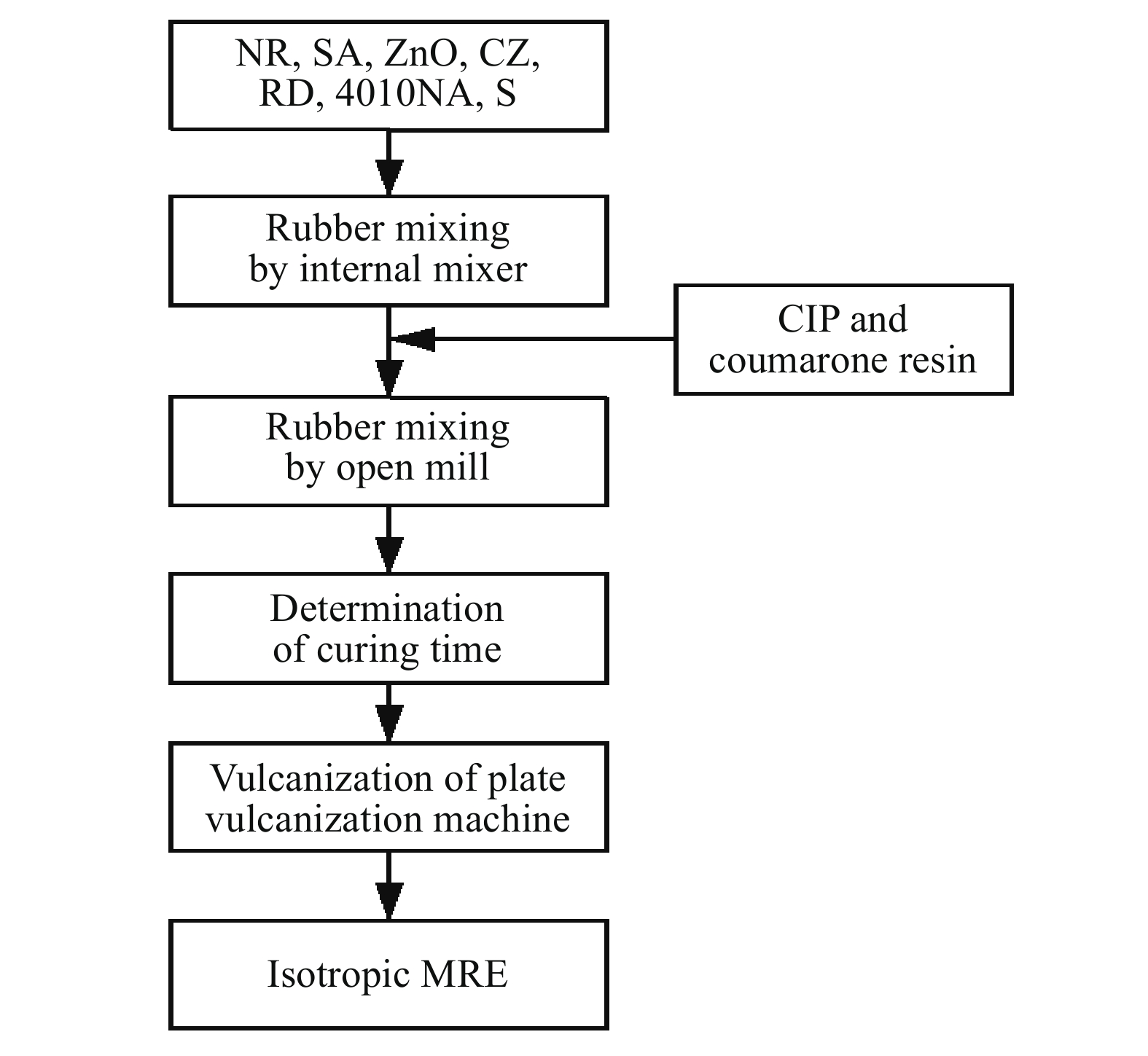
表 1 MRE的成分配比
Table 1. Composition of MRE
g Coumarone resin SA ZnO CZ RD 4010NA S NR CIP 12 1 5 0.5 3 2 3 100 190 12 1 5 0.5 3 2 3 100 506 
下載: 導出CSV
表 2 Bouc?Wen模型識別結果及吻合率
Table 2. Identified values and fitness values of the Bouc?Wen model
B/ mT f/Hz xm/% fitness values k c α A γ β n 0 1 1.36 0.9730 6.1106 5.9804 0.5310 39.9773 11.3493 2.3570 0.7731 0 1 2.51 0.9681 4.4045 3.5773 0.6137 54.4966 17.0611 3.0967 0.5451 0 1 4.64 0.9565 2.6280 3.0000 0.6595 74.9881 12.5262 2.2414 0.9174 0 1 8.57 0.9467 1.8639 2.6686 0.4699 45.5637 11.5298 1.3959 0.5629 0 1 15.8 0.9397 2.7776 1.0000 0.6278 54.0000 12.8755 4.7350 0.8254 0 1 29.3 0.9430 1.0000 0.1139 0.3029 72.0000 8.0525 0.5736 1.1378 405 0.5 0.40 0.9554 9.8393 17.0504 0.1054 57.1985 15.1242 1.7420 0.1000 405 1 0.40 0.9419 11.2673 15.0000 0.4228 73.6573 14.6013 2.6526 0.5289 405 3 0.40 0.9765 7.9062 8.3759 0.0038 73.8195 9.9851 4.6420 0.8466 405 5 0.40 0.9741 11.7603 4.8326 0.0864 59.9666 11.5887 1.5288 0.3563 115 1 2.51 0.9461 4.4521 5.9309 0.4151 46.3326 12.5141 2.0746 1.3497 234 1 2.51 0.9409 4.7443 9.0000 0.4838 70.0000 13.4964 1.8649 1.3741 405 1 2.51 0.9386 6.4304 13.7396 0.6064 80.0000 6.6630 1.2085 1.3839 456 1 2.51 0.9344 6.2437 9.1639 0.3505 70.0000 18.7092 5.6384 0.6457 545 1 2.51 0.9380 6.0084 10.3366 0.2640 66.8783 16.8824 1.0650 1.2103
下載: 導出CSV
表 3 改進Bouc?Wen模型識別結果及吻合率
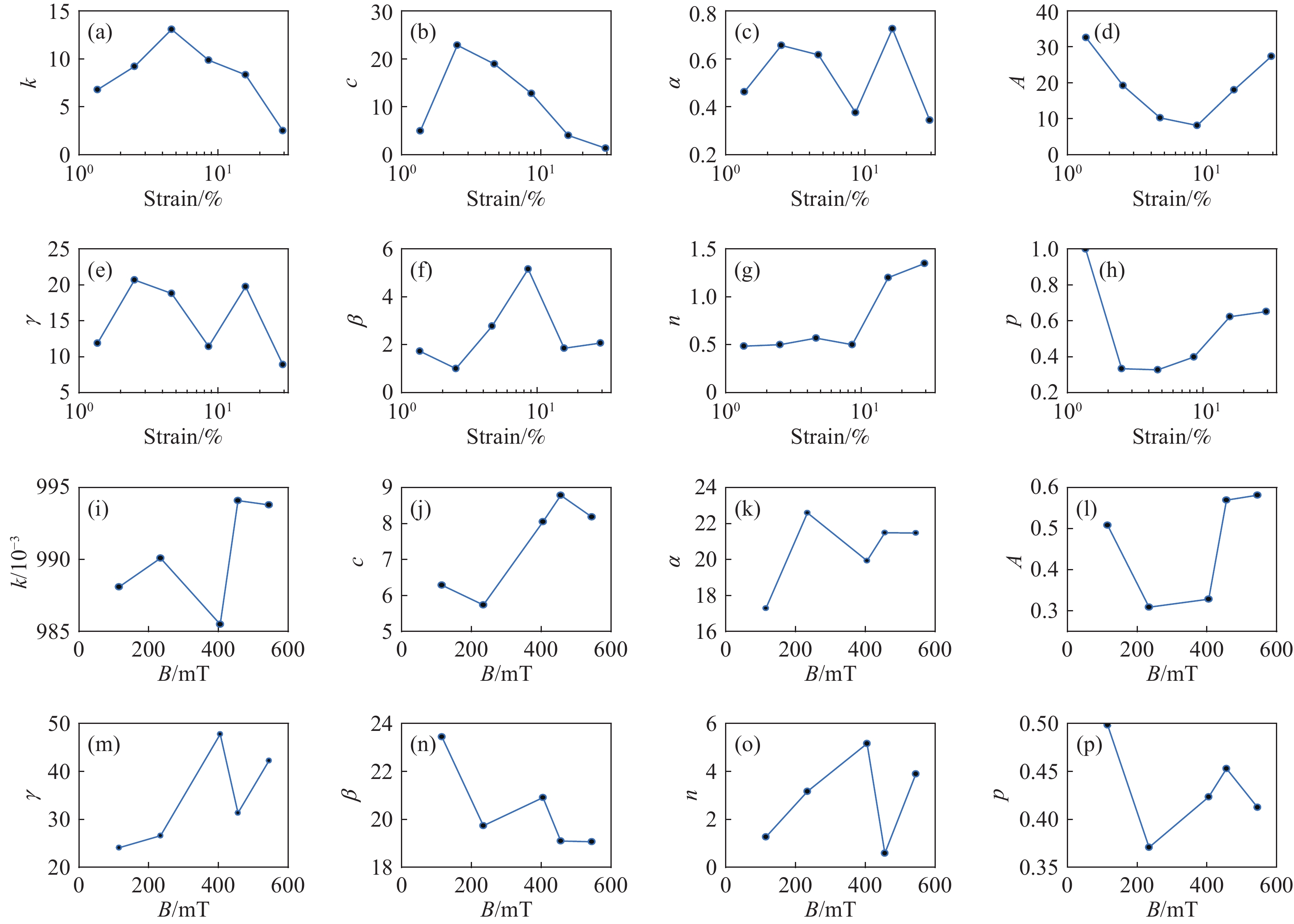
Table 3. Identified values and fitness values of the modified Bouc?Wen model
B/ mT f/Hz xm/% fitness values k c α A γ β n p 0 1 1.36 0.9831 6.7864 4.9731 0.4624 32.5858 11.8852 1.7276 0.4847 1.0000 0 1 2.51 0.9904 9.2082 22.8462 0.6561 19.2403 20.6769 1.0023 0.5000 0.3334 0 1 4.64 0.9928 13.0716 18.9248 0.6167 10.2625 18.8049 2.7732 0.5684 0.3270 0 1 8.57 0.9884 9.8591 12.7818 0.3759 8.1462 11.4349 5.1525 0.5000 0.3984 0 1 15.8 0.9887 8.3377 4.0287 0.7254 18.0359 19.7456 1.8512 1.1993 0.6228 0 1 29.3 0.9802 2.5102 1.3608 0.3440 27.3639 8.9086 2.0680 1.3468 0.6513 405 0.5 0.40 0.9924 19.0175 34.0650 0.6236 61.4151 21.0888 1.0865 0.7105 1.0000 405 1 0.40 0.9918 19.8181 22.6808 0.5380 49.3512 19.723 2.5815 0.6600 0.9000 405 3 0.40 0.9955 18.2508 24.4390 0.5066 52.4992 2.3542 2.6633 1.2512 0.7043 405 5 0.40 0.9957 11.8541 22.7924 0.3706 69.4789 4.5770 3.4270 1.4916 0.6600 115 1 2.51 0.9881 6.2890 17.2922 0.5086 24.0852 23.4419 1.2659 0.4984 0.3998 234 1 2.51 0.9901 5.7381 22.5996 0.3092 26.5923 19.7345 3.1640 0.3708 0.4425 405 1 2.51 0.9855 8.0516 19.9349 0.3287 47.7665 20.9086 5.1609 0.4234 0.6927 456 1 2.51 0.9941 8.7869 21.4934 0.5697 31.3416 19.0964 0.5867 0.4529 0.6205 545 1 2.51 0.9938 8.1853 21.4785 0.5817 42.2406 19.0661 3.8937 0.4125 0.6129
下載: 導出CSV
www.77susu.com<span id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> <span id="fpn9h"><noframes id="fpn9h"> <th id="fpn9h"></th> <strike id="fpn9h"><noframes id="fpn9h"><strike id="fpn9h"></strike> <th id="fpn9h"><noframes id="fpn9h"> <span id="fpn9h"><video id="fpn9h"></video></span> <ruby id="fpn9h"></ruby> <strike id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> -
參考文獻
[1] Dong X F, Ma N, Qi M, et al. The pressure-dependent MR effect of magnetorheological elastomers. Smart Mater Struct, 2012, 21(7): 075014 doi: 10.1088/0964-1726/21/7/075014 [2] Ahamed R, Choi S B, Ferdaus M M. A state of art on magneto-rheological materials and their potential applications. J Intell Mater Syst Struct, 2018, 29(10): 2051 doi: 10.1177/1045389X18754350 [3] An J S, Kwon S H, Choi H J, et al. Modified silane-coated carbonyl iron/natural rubber composite elastomer and its magnetorheological performance. Compos Struct, 2017, 160: 1020 doi: 10.1016/j.compstruct.2016.10.128 [4] Tong Y, Dong X F, Qi M. Improved tunable range of the field-induced storage modulus by using flower-like particles as the active phase of magnetorheological elastomers. Soft Matter, 2018, 14(18): 3504 doi: 10.1039/C8SM00359A [5] Jolly M R, Carlson J D, Mu?oz B C. A model of the behaviour of magnetorheological materials. Smart Mater Struct, 1996, 5(5): 607 doi: 10.1088/0964-1726/5/5/009 [6] Davis L C. Model of magnetorheological elastomers. J Appl Phys, 1999, 85(6): 3348 doi: 10.1063/1.369682 [7] Chen L, Gong X L, Li W H. Microstructures and viscoelastic properties of anisotropic magnetorheological elastomers. Smart Mater Struct, 2007, 16(6): 2645 doi: 10.1088/0964-1726/16/6/069 [8] Zhang X Z, Peng S L, Wen W J, et al. Analysis and fabrication of patterned magnetorheological elastomers. Smart Mater Struct, 2008, 17(4): 045001 doi: 10.1088/0964-1726/17/4/045001 [9] Wang B C, Kari L. A visco-elastic-plastic constitutive model of isotropic magneto-sensitive rubber with amplitude, frequency and magnetic dependency. Int J Plast, 2020, 132: 102756 doi: 10.1016/j.ijplas.2020.102756 [10] Li W H, Zhou Y, Tian T F. Viscoelastic properties of MR elastomers under harmonic loading. Rheol Acta, 2010, 49(7): 733 doi: 10.1007/s00397-010-0446-9 [11] Kari L, Blom P. Magneto-sensitive rubber in a noise reduction context: Exploring the potential. Plast Rubber Compos, 2005, 34(8): 365 doi: 10.1179/174328905X59692 [12] Chen L, Jerrams S. A rheological model of the dynamic behavior of magnetorheological elastomers. J Appl Phys, 2011, 110(1): 013513 doi: 10.1063/1.3603052 [13] Blom P, Kari L. A nonlinear constitutive audio frequency magneto-sensitive rubber model including amplitude, frequency and magnetic field dependence. J Sound Vib, 2011, 330(5): 947 doi: 10.1016/j.jsv.2010.09.010 [14] Xu Z D, Xu C, Hu J. Equivalent fractional Kelvin model and experimental study on viscoelastic damper. J Vib Control, 2015, 21(13): 2536 doi: 10.1177/1077546313513604 [15] Xu Z D, Shen Y P, Guo Y Q. Semi-active control of structures incorporated with magnetorheological dampers using neural networks. Smart Mater Struct, 2003, 12(1): 80 doi: 10.1088/0964-1726/12/1/309 [16] Behrooz M, Wang X J, Gordaninejad F. Modeling of a new semi-active/passive magnetorheological elastomer isolator. Smart Mater Struct, 2014, 23(4): 045013 doi: 10.1088/0964-1726/23/4/045013 [17] Xu Z D, Suo S, Zhu J T, et al. Performance tests and modeling on high damping magnetorheological elastomers based on bromobutyl rubber. J Intell Mater Syst Struct, 2018, 29(6): 1025 doi: 10.1177/1045389X17730909 [18] Wang B C, Kari L. A nonlinear constitutive model by spring, fractional derivative and modified bounding surface model to represent the amplitude, frequency and the magnetic dependency for Magneto-sensitive rubber. J Sound Vib, 2019, 438: 344 doi: 10.1016/j.jsv.2018.09.028 [19] Kong F, Hou Z X, Xu J, et al. Steady-state response determination of a hysteretic system endowed with fractional elements via a multi-harmonic balance method. J Vib Eng, 2021, 34(3): 552孔凡, 侯召旭, 徐軍, 等. 基于多諧波平衡法的滯回分數階系統穩態動力響應. 振動工程學報, 2021, 34(3):552 [20] Wang B C, Kari L. Modeling and vibration control of a smart vibration isolation system based on magneto-sensitive rubber. Smart Mater Struct, 2019, 28(6): 065026 doi: 10.1088/1361-665X/ab1ab4 [21] Dominguez A, Sedaghati R, Stiharu I. Modelling the hysteresis phenomenon of magnetorheological dampers. Smart Mater Struct, 2004, 13(6): 1351 doi: 10.1088/0964-1726/13/6/008 [22] Yang J, Du H P, Li W H, et al. Experimental study and modeling of a novel magnetorheological elastomer isolator. Smart Mater Struct, 2013, 22(11): 117001 doi: 10.1088/0964-1726/22/11/117001 [23] Zhao Y W, Liu Y Q, Yang S P, et al. An improved Bouc-Wen model for describing hysteretic characteristics of shock absorbers. Chin J Eng, 2020, 42(10): 10趙義偉, 劉永強, 楊紹普, 等. 一種描述減振器滯回特性的Bouc?Wen改進模型. 工程科學學報, 2020, 42(10):10 [24] Xu Z D, Li A Q, Cheng W R, et al. A temperature phenomenological model with mass element of magnetorheological damper. Eng Mech, 2005, 22(2): 144 doi: 10.3969/j.issn.1000-4750.2005.02.026徐趙東, 李愛群, 程文瀼, 等. 磁流變阻尼器帶質量元素的溫度唯象模型. 工程力學, 2005, 22(2):144 doi: 10.3969/j.issn.1000-4750.2005.02.026 [25] Wang Q, Dong X F, Li L Y, et al. A nonlinear model of magnetorheological elastomer with wide amplitude range and variable frequencies. Smart Mater Struct, 2017, 26(6): 065010 doi: 10.1088/1361-665X/aa66e3 [26] Chang Y J, Tian W W, Chen E L, et al. Dynamic model for the nonlinear hysteresis of metal rubber based on the fractional-order derivative. J Vib Shock, 2020, 39(14): 233常宇健, 田沃沃, 陳恩利, 等. 基于分數階微分的金屬橡膠遲滯非線性動力學模型. 振動與沖擊, 2020, 39(14):233 [27] You H, Shen Y J, Xing H J, et al. Optimal control and parameters design for the fractional-order vehicle suspension system. J Low Freq Noise Vib Active Control, 2018, 37(3): 456 doi: 10.1177/0263092317717166 [28] Xue D Y, Zhao C N, Chen Y Q. A modified approximation method of fractional order system // 2006 International Conference on Mechatronics and Automation. Luoyang, 2006: 1043 [29] Liu Y Y, Dai J J, Zhao S S, et al. Optimization of five-parameter BRDF model based on hybrid GA-PSO algorithm. Optik, 2020, 219: 164978 doi: 10.1016/j.ijleo.2020.164978 [30] Liu Y Q, Yang S P, Liao Y Y. A new method of parameters identification for magnetorheological damper model. J Mech Eng, 2018, 54(6): 62 doi: 10.3901/JME.2018.06.062劉永強, 楊紹普, 廖英英. 一種磁流變阻尼器模型參數識別新方法. 機械工程學報, 2018, 54(6):62 doi: 10.3901/JME.2018.06.062 -
點擊查看大圖
計量
- 文章訪問數: 622
- HTML全文瀏覽量: 337
- PDF下載量: 59
- 被引次數: 0
