Analytical solutions of fracture parameters for a centrally cracked Brazilian disk considering the loading friction
-
摘要: 運用權函數法推導出考慮加載端摩擦的四種形式分布載荷加載下，中心直裂紋巴西圓盤試樣在任意I/II復合型斷裂模式下I、II型應力強度因子及T應力的解析解，并探究了端部摩擦及載荷分布角度對斷裂參數的影響。研究結果表明：（1）當中心裂紋相對長度β較小時，純I型、純II型斷裂的YI、YII及T*（分別是量綱為一的I型、II型應力強度因子及T應力）均隨摩擦系數及載荷分布角度增大而減小；但是，當β較大時，摩擦系數增大可使純I型YI增大，而載荷分布角度增大可使純II型T*增大。（2）接觸載荷分布形式為常數函數時，載荷分布角度對斷裂參數的影響最顯著，而四次函數下其對斷裂參數的影響相對最小。（3）當β較小時，純II型加載角度隨載荷分布角度增大而減小；當β較大時，其隨載荷分布角度增大而增大；摩擦系數增大可使純II型加載角度增大。Abstract: A centrally cracked Brazilian disk (CCBD) specimen subjected to a pair of diametral compressive forces has been widely used to study mixed-mode I and II fractures of brittle and quasi-brittle materials. Reasons for using the CCBD are mainly due to its capability to introduce different mode mixities from pure mode I to pure mode II, the existence of closed-form solutions for fracture parameters, and the simple setup of compressive test. In addition to the diametrical concentrated force loading, the partially distributed pressure loading is also an important loading condition for CCBD specimen tests. Using the weight function method, analytical solutions of stress intensity factors and T stress considering the tangential loading friction for a CCBD specimen that is subjected to four typical partially distributed loads were derived, and effects of the boundary friction and load distribution angle on the fracture parameters were also explored. The results obtained are as follows: (1) For short cracks, geometric parameters YI, YII, and T* of pure mode I and II fractures decrease with an increase in the friction coefficient and load distribution angle. However, for long cracks, an increase in the friction coefficient causes an increase in pure mode-I YI, and an increase in the load distribution angle causes an increase in pure mode-II T*; (2) The influence of the load distribution angle on the fracture parameters is the most significant when the distributed pressure follows a constant function form, while it is the least significant for the case of quartic polynomial pressure; (3) The critical loading angle for pure mode II fractures decreases with an increase in the load distribution angle for short cracks, whereas it increases for long cracks. When the load distribution angle is fixed, an increase in friction can raise the critical loading angle for pure mode II fractures. These results have further improved the research of fracture parameters in CCBD specimens.
-
圖 1 CCBD試樣與BD試樣示意圖。(a) CCBD試樣；(b) BD試樣
Figure 1. Schematic of (a) centrally cracked Brazilian disk and (b) Brazilian disk specimens
圖 2 圓盤邊界上(r=R)式(13)計算結果與q(θ)的對比
Figure 2. Comparison between the calculated results based on Eq. (13) and the applied normal pressures q(θ)
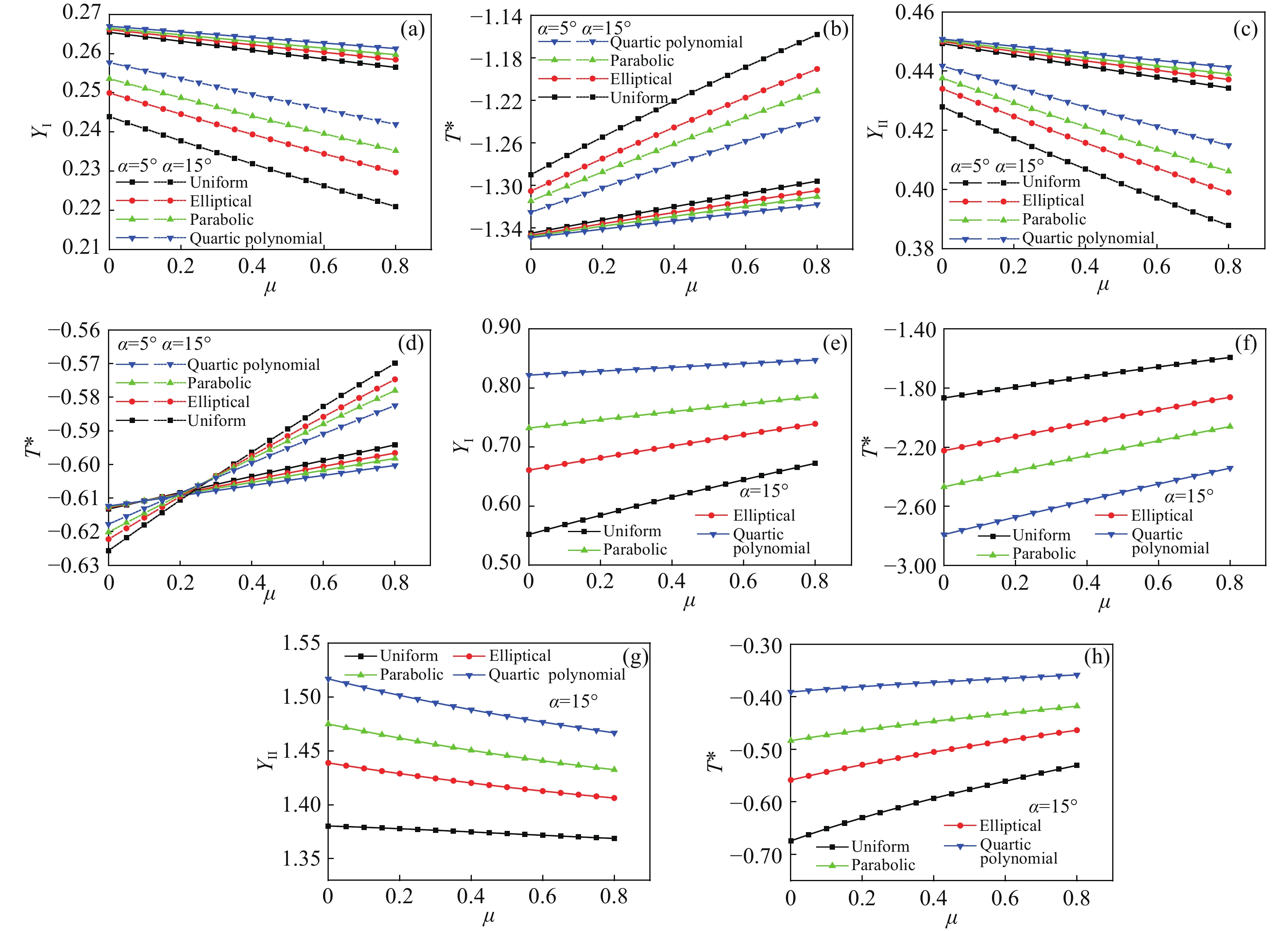
圖 4 純I型及純II型斷裂的幾何參數隨摩擦系數的變化特征。（a） β=0.2：純I型YI；（b）β=0.2：純I型T*；（c）β=0.2：純II型YII；（d） β=0.2：純II型T*；（e）β=0.8：純I型YI；（f）β=0.8：純I型T*；（g） β=0.8：純II型YII；（h）β=0.8：純II型T*
Figure 4. Variations in the YI, YII and T* of pure mode I and II fractures versus friction coefficient μ: (a) β=0.2: pure mode-I YI; (b) β=0.2: pure mode-I T*; (c) β=0.2: pure mode-II YII; (d) β=0.2: pure mode-II T*; (e) β=0.8: pure mode-I YI; (f) β=0.8: pure mode-I T*; (g) β=0.8: pure mode-II YII; (h) β=0.8: pure mode-II T*
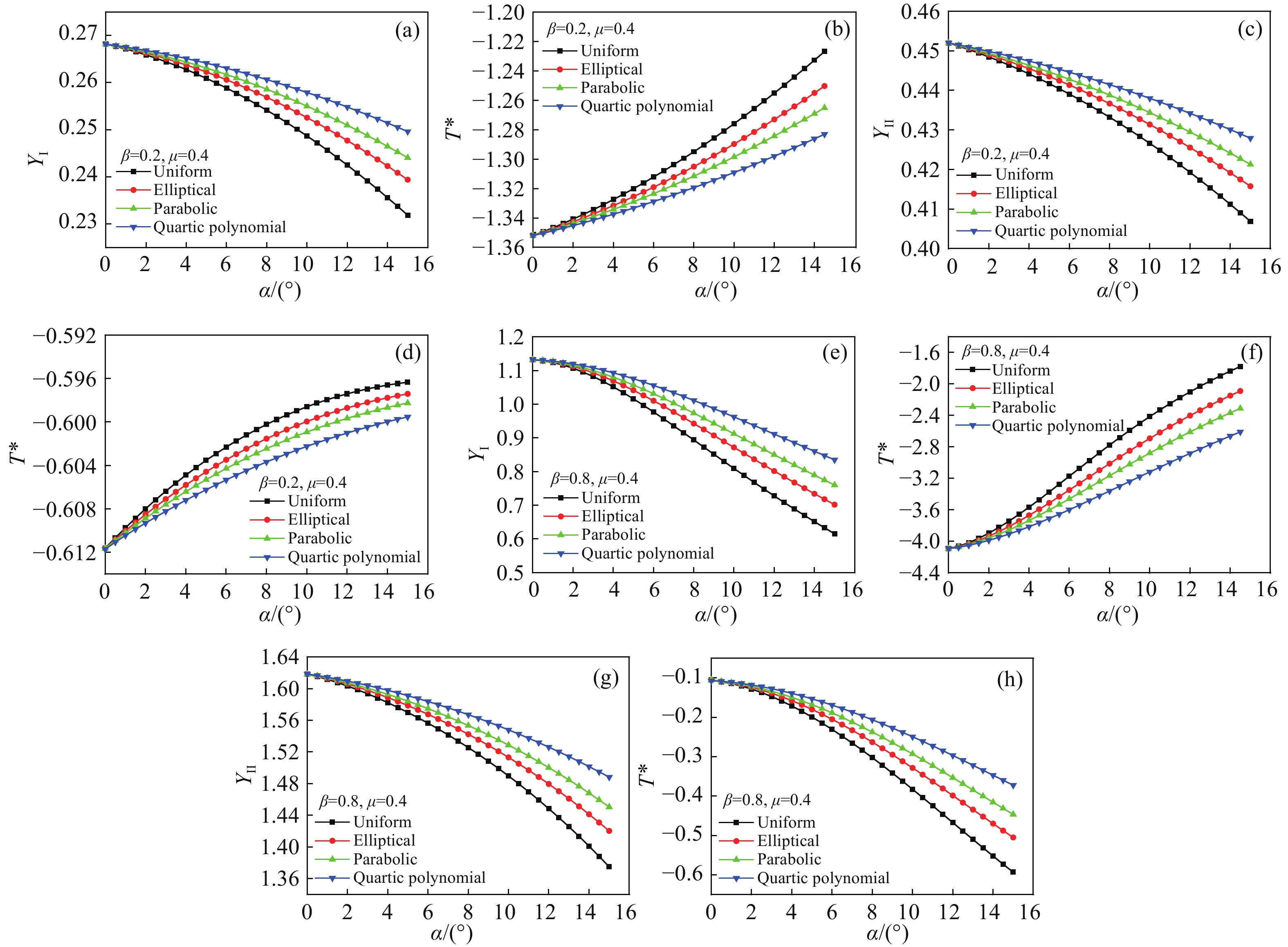
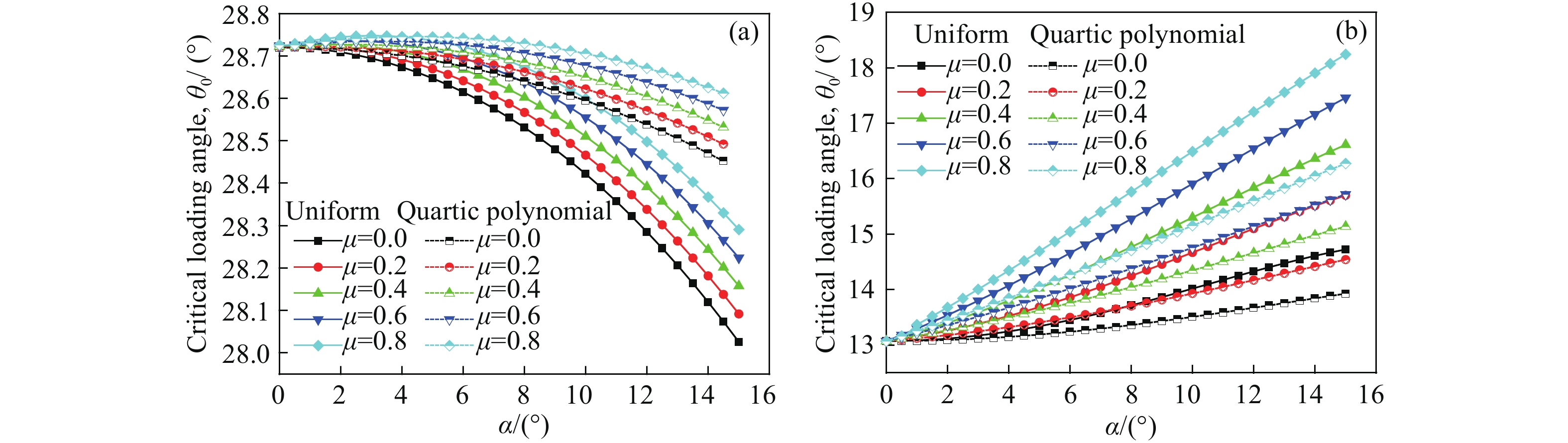
圖 5 純I型及純II型斷裂的幾何參數隨載荷分布角度的變化特征。（a） β=0.2：純I型YI；（b）β=0.2：純I型T*；（c）β=0.2：純II型YII；（d） β=0.2：純II型T*；（e）β=0.8: 純I型YI；（f）β=0.8：純I型T*；（g） β=0.8：純II型YII；（h）β=0.8：純II型T*
Figure 5. Variations in the YI, YII, and T* of pure mode I and II fractures versus the load distribution angle α: (a) β = 0.2: pure mode-I YI; (b) β = 0.2: pure mode-I T*; (c) β = 0.2: pure mode-II YII; (d) β = 0.2: pure mode-II T*; (e) β = 0.8: pure mode-I YI; (f) β = 0.8: pure mode-I T*; (g) β = 0.8: pure mode-II YII; (h) β = 0.8: pure mode-II T*
圖 6 載荷分布角度對純II型加載角度的影響。（a）β=0.2；（b） β=0.8
Figure 6. Effect of the load distribution angle on the critical loading angle for pure mode II fractures: (a) β = 0.2; (b) β = 0.8
表 1 分布載荷加載下巴西圓盤應力解析解的系數
Table 1. Series coefficients Cn of the stress analytical solutions for the Brazilian disk subjected to distributed pressures
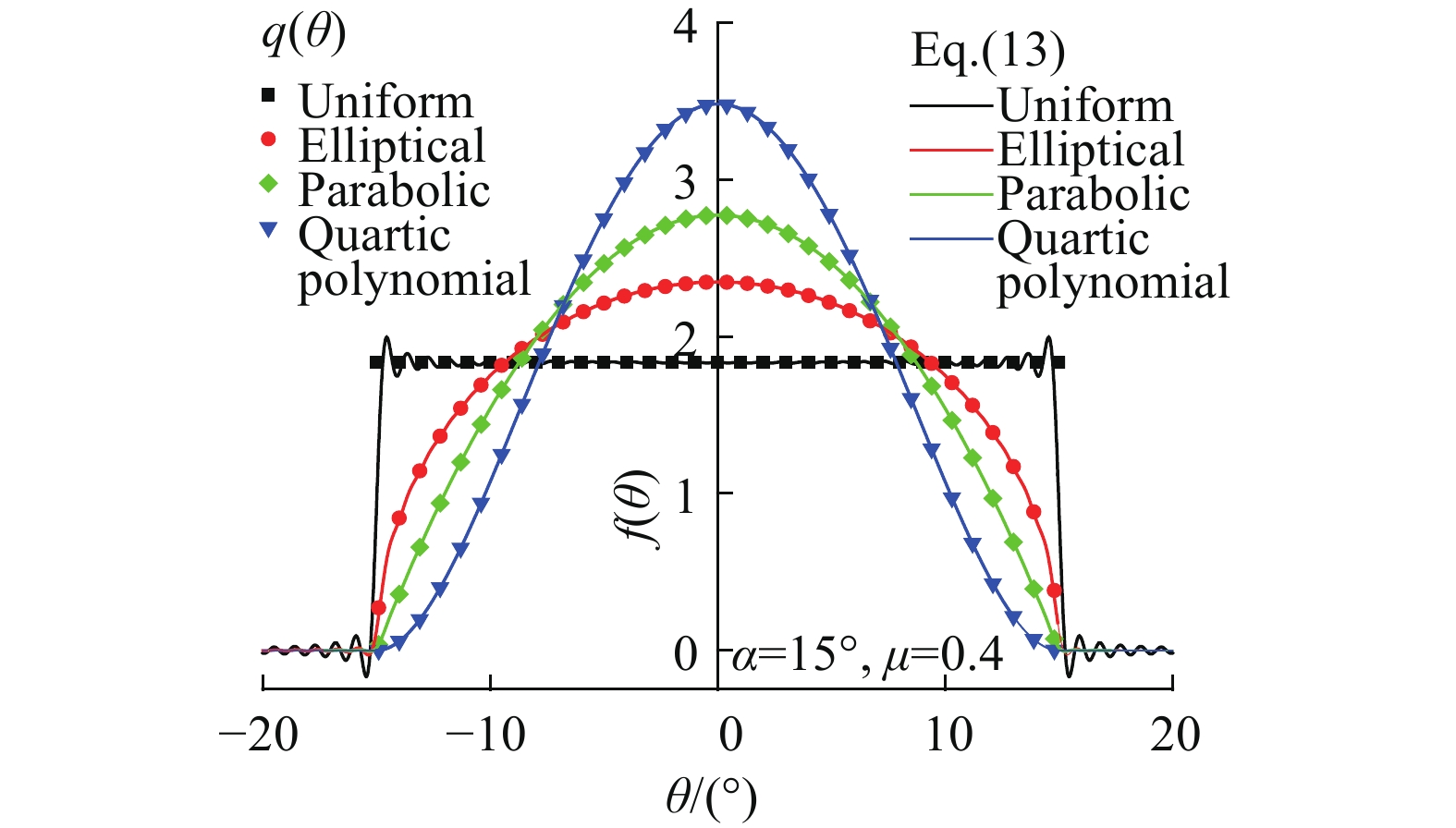
Distribution form f(θ)/qmax qmax C0 Cn (n=±1, ±2, ···) Uniform 1 $ {[2(\sin \alpha + \mu (1 - \cos \alpha ))]^{ - 1}} $ $ \dfrac{{2\alpha }}{{\text{π}} }{q_{\max }} $ $ {q_{\max }}\dfrac{{\sin 2n\alpha - 2\mu {{(\sin n\alpha )}^2}}}{{n{\text{π}} }} $ Elliptical $ {\left(1 - {\left(\dfrac{\theta }{\alpha }\right)^2}\right)^{1/2}} $ $ {[{\text{π}} ({J_1}(\alpha ) + \mu {H_1}(\alpha ))]^{ - 1}} $ $ \dfrac{\alpha }{2}{q_{\max }} $ $ {q_{\max }}\dfrac{{{J_1}(2n\alpha ) - \mu {H_1}(2n\alpha )}}{{2n}} $ Parabolic $ 1 - {\left(\dfrac{\theta }{\alpha }\right)^2} $ $ \begin{gathered} {\alpha ^2}[4\mu (1 + {\alpha ^2}/2 - \alpha \sin \alpha - \\ \cos \alpha ) + 4\sin \alpha - 4\alpha \cos \alpha {]^{ - 1}} \\ \end{gathered} $ $ \dfrac{{4\alpha }}{{3{\text{π}} }}{q_{\max }} $ $\begin{gathered} {q_{\max } }[\mu (2\alpha n\sin 2n\alpha + \cos 2n\alpha - 2{\alpha ^2}{n^2} - 1)+ \\ \sin 2n\alpha - 2\alpha n\cos 2n\alpha ]/(2{\text{π} } {\alpha ^2}{n^3}) \\ \end{gathered}$ Quartic polynomial $ {\left(1 - {\left(\dfrac{\theta }{\alpha }\right)^2}\right)^2} $ $\begin{gathered} {\alpha ^4}[16(3 - {\alpha ^2})\sin \alpha - 48\alpha \cos \alpha + \\ 2\mu ({\alpha ^4} + 4{\alpha ^2} + 24 + \\ 8({\alpha ^2} - 3)\cos \alpha - 24\alpha \sin \alpha ){]^{ - 1} } \\ \end{gathered}$ $ \dfrac{{16\alpha }}{{15{\text{π}} }}{q_{\max }} $ $ \begin{gathered} {q_{\max }}[(3\mu - 4{\alpha ^2}{n^2}\mu - 6\alpha n)\cos 2n\alpha + \\ (6\alpha n\mu + 3 - 4{\alpha ^2}{n^2})\sin 2n\alpha - \\ 2\mu ({\alpha ^4}{n^4} + {\alpha ^2}{n^2} + 3/2)]/(2{\text{π}} {n^5}{\alpha ^4}) \\ \end{gathered} $ 
下載: 導出CSV
www.77susu.com<span id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> <span id="fpn9h"><noframes id="fpn9h"> <th id="fpn9h"></th> <strike id="fpn9h"><noframes id="fpn9h"><strike id="fpn9h"></strike> <th id="fpn9h"><noframes id="fpn9h"> <span id="fpn9h"><video id="fpn9h"></video></span> <ruby id="fpn9h"></ruby> <strike id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> -
參考文獻
[1] Atkinson C, Smelser R E, Sanchez J. Combined mode fracture via the cracked Brazilian disk test. Int J Fract, 1982, 18(4): 279 doi: 10.1007/BF00015688 [2] Fett T. T-stresses in rectangular plates and circular disks. Eng Fract Mech, 1998, 60(5-6): 631 doi: 10.1016/S0013-7944(98)00038-1 [3] Fett T. Stress intensity factors and T-stress for single and double-edge-cracked circular disks under mixed boundary conditions. Eng Fract Mech, 2002, 69(1): 69 doi: 10.1016/S0013-7944(01)00078-9 [4] Dong S M, Wang Y, Xia Y M. Stress intensity factors for central cracked circular disk subjected to compression. Eng Fract Mech, 2004, 71(7-8): 1135 doi: 10.1016/S0013-7944(03)00120-6 [5] Akbardoost J, Rastin A. Comprehensive data for calculating the higher order terms of crack tip stress field in disk-type specimens under mixed mode loading. Theor Appl Fract Mech, 2015, 76: 75 doi: 10.1016/j.tafmec.2015.01.004 [6] Smith D J, Ayatollahi M R, Pavier M J. The role of T-stress in brittle fracture for linear elastic materials under mixed-mode loading. Fatigue Fract Eng Mater Struct, 2001, 24(2): 137 doi: 10.1046/j.1460-2695.2001.00377.x [7] Dong Z, Tang S B, Lang Y X. Hydraulic fracture prediction theory based on the minimum strain energy density criterion. Chin J Eng, 2019, 41(4): 436董卓, 唐世斌, 郎穎嫻. 基于最小應變能密度因子斷裂準則的巖石裂紋水力壓裂研究. 工程科學學報, 2019, 41(4):436 [8] Liu H Y. Initiation mechanism of cracks of rock in compression and shear considering T-stress. Chin J Geotech Eng, 2019, 41(7): 1296劉紅巖. 考慮T應力的巖石壓剪裂紋起裂機理. 巖土工程學報, 2019, 41(7):1296 [9] Ayatollahi M R, Aliha M R M. Mixed mode fracture in soda lime glass analyzed by using the generalized MTS criterion. Int J Solids Struct, 2009, 46(2): 311 doi: 10.1016/j.ijsolstr.2008.08.035 [10] Aliha M R M, Ayatollahi M R. Analysis of fracture initiation angle in some cracked ceramics using the generalized maximum tangential stress criterion. Int J Solids Struct, 2012, 49(13): 1877 doi: 10.1016/j.ijsolstr.2012.03.029 [11] Ayatollahi M R, Aliha M R M. On the use of Brazilian disc specimen for calculating mixed mode I-II fracture toughness of rock materials. Eng Fract Mech, 2008, 75(16): 4631 doi: 10.1016/j.engfracmech.2008.06.018 [12] Hua W, Dong S M, Peng F, et al. Experimental investigation on the effect of wetting-drying cycles on mixed mode fracture toughness of sandstone. Int J Rock Mech Min Sci, 2017, 93: 242 doi: 10.1016/j.ijrmms.2017.01.017 [13] Yin T B, Wu Y, Wang C, et al. Mixed-mode I + II tensile fracture analysis of thermally treated granite using straight-through notch Brazilian disc specimens. Eng Fract Mech, 2020, 234: 107111 doi: 10.1016/j.engfracmech.2020.107111 [14] Awaji H, Sato S. Combined mode fracture toughness measurement by the disk test. J Eng Mater Technol, 1978, 100(2): 175 doi: 10.1115/1.3443468 [15] Dorogoy A, Banks-Sills L. Effect of crack face contact and friction on Brazilian disk specimens—A finite difference solution. Eng Fract Mech, 2005, 72(18): 2758 doi: 10.1016/j.engfracmech.2005.05.005 [16] Ayatollahi M R, Aliha M R M. Wide range data for crack tip parameters in two disc-type specimens under mixed mode loading. Comput Mater Sci, 2007, 38(4): 660 doi: 10.1016/j.commatsci.2006.04.008 [17] Xu J G, Dong S M, Hua W. Effect of confining pressure on stress intensity factors determined by cracked Brazilian disk. Rock Soil Mech, 2015, 36(7): 1959徐積剛, 董世明, 華文. 圍壓對巴西裂紋圓盤應力強度因子影響分析. 巖土力學, 2015, 36(7):1959 [18] Hua W, Xu J G, Dong S M, et al. Effect of confining pressure on stress intensity factors for cracked Brazilian disk. Int J Appl Mechanics, 2015, 7(3): 1550051 doi: 10.1142/S1758825115500519 [19] Hua W, Li Y F, Dong S M, et al. T-stress for a centrally cracked Brazilian disk under confining pressure. Eng Fract Mech, 2015, 149: 37 doi: 10.1016/j.engfracmech.2015.09.048 [20] Hou C, Wang Z Y, Liang W G, et al. Determination of fracture parameters in center cracked circular discs of concrete under diametral loading: A numerical analysis and experimental results. Theor Appl Fract Mech, 2016, 85: 355 doi: 10.1016/j.tafmec.2016.04.006 [21] Li Y F, Dong S M, Hua W. T-stress for central cracked Brazilian disk subjected to compression. Rock Soil Mech, 2016, 37(11): 3191李一凡, 董世明, 華文. 中心裂紋巴西圓盤壓縮載荷下T應力研究. 巖土力學, 2016, 37(11):3191 [22] Hou C, Wang Z Y, Liang W G, et al. Investigation of the effects of confining pressure on SIFs and T-stress for CCBD specimens using the XFEM and the interaction integral method. Eng Fract Mech, 2017, 178: 279 doi: 10.1016/j.engfracmech.2017.03.049 [23] Tang S B. Stress intensity factors for a Brazilian disc with a central crack subjected to compression. Int J Rock Mech Min Sci, 2017, 93: 38 doi: 10.1016/j.ijrmms.2017.01.003 [24] Dong Z, Tang S B. Effect of confining pressure and diametrical force on stress intensity fracture in central cracked disk. Chin J Comput Mech, 2018, 35(2): 168 doi: 10.7511/jslx20170221001董卓, 唐世斌. 圍壓與徑向荷載共同作用下巴西盤裂紋應力強度因子的解析解. 計算力學學報, 2018, 35(2):168 doi: 10.7511/jslx20170221001 [25] Markides C F, Pazis D N, Kourkoulis S K. Stress intensity factors for the Brazilian disc with a short central crack: Opening versus closing cracks. Appl Math Model, 2011, 35(12): 5636 doi: 10.1016/j.apm.2011.05.013 [26] Hondros G. The evaluation of Poisson's ratio and the modulus of materials of low tensile resistance by the Brazilian (indirect tensile) test with particular reference to concrete. Australian J Appl Sci, 1959, 10(3): 243 [27] Fairhurst C. On the validity of the ‘Brazilian’ test for brittle materials. Int J Rock Mech Min Sci Geomech Abstr, 1964, 1(4): 535 doi: 10.1016/0148-9062(64)90060-9 [28] Hung K M, Ma C C. Theoretical analysis and digital photoelastic measurement of circular disks subjected to partially distributed compressions. Exp Mech, 2003, 43(2): 216 [29] Wei X X, Chau K T. Three dimensional analytical solution for finite circular cylinders subjected to indirect tensile test. Int J Solids Struct, 2013, 50(14-15): 2395 doi: 10.1016/j.ijsolstr.2013.03.026 [30] Japaridze L. Stress-deformed state of cylindrical specimens during indirect tensile strength testing. J Rock Mech Geotech Eng, 2015, 7(5): 509 doi: 10.1016/j.jrmge.2015.06.006 [31] Yu J H, Shang X C, Wu P F. Influence of pressure distribution and friction on determining mechanical properties in the Brazilian test: Theory and experiment. Int J Solids Struct, 2019, 161: 11 doi: 10.1016/j.ijsolstr.2018.11.002 [32] Markides C F, Kourkoulis S K. The stress field in a standardized Brazilian disc: The influence of the loading type acting on the actual contact length. Rock Mech Rock Eng, 2012, 45(2): 145 doi: 10.1007/s00603-011-0201-2 [33] Kourkoulis S K, Markides C F, Chatzistergos P E. The Brazilian disc under parabolically varying load: Theoretical and experimental study of the displacement field. Int J Solids Struct, 2012, 49(7-8): 959 doi: 10.1016/j.ijsolstr.2011.12.013 [34] Yu J H, Shang X C. Analysis of the influence of boundary pressure and friction on determining fracture toughness of shale using cracked Brazilian disc test. Eng Fract Mech, 2019, 212: 57 doi: 10.1016/j.engfracmech.2019.03.009 -
點擊查看大圖
圖(6) / 表(1)
計量
- 文章訪問數: 645
- HTML全文瀏覽量: 337
- PDF下載量: 44
- 被引次數: 0
