Coordinated variable-based guidance method and experimental verification for multi-UAVs
-
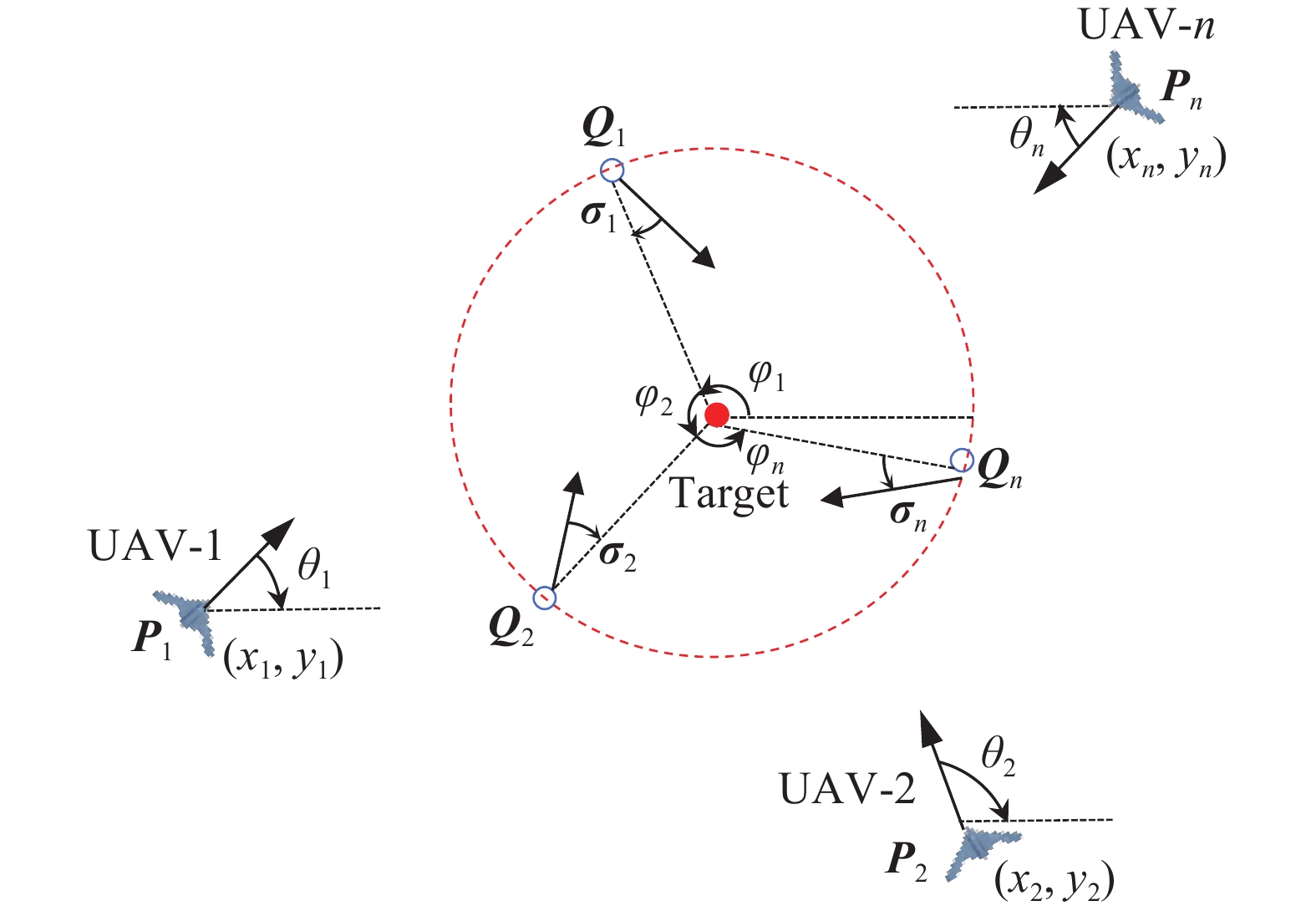
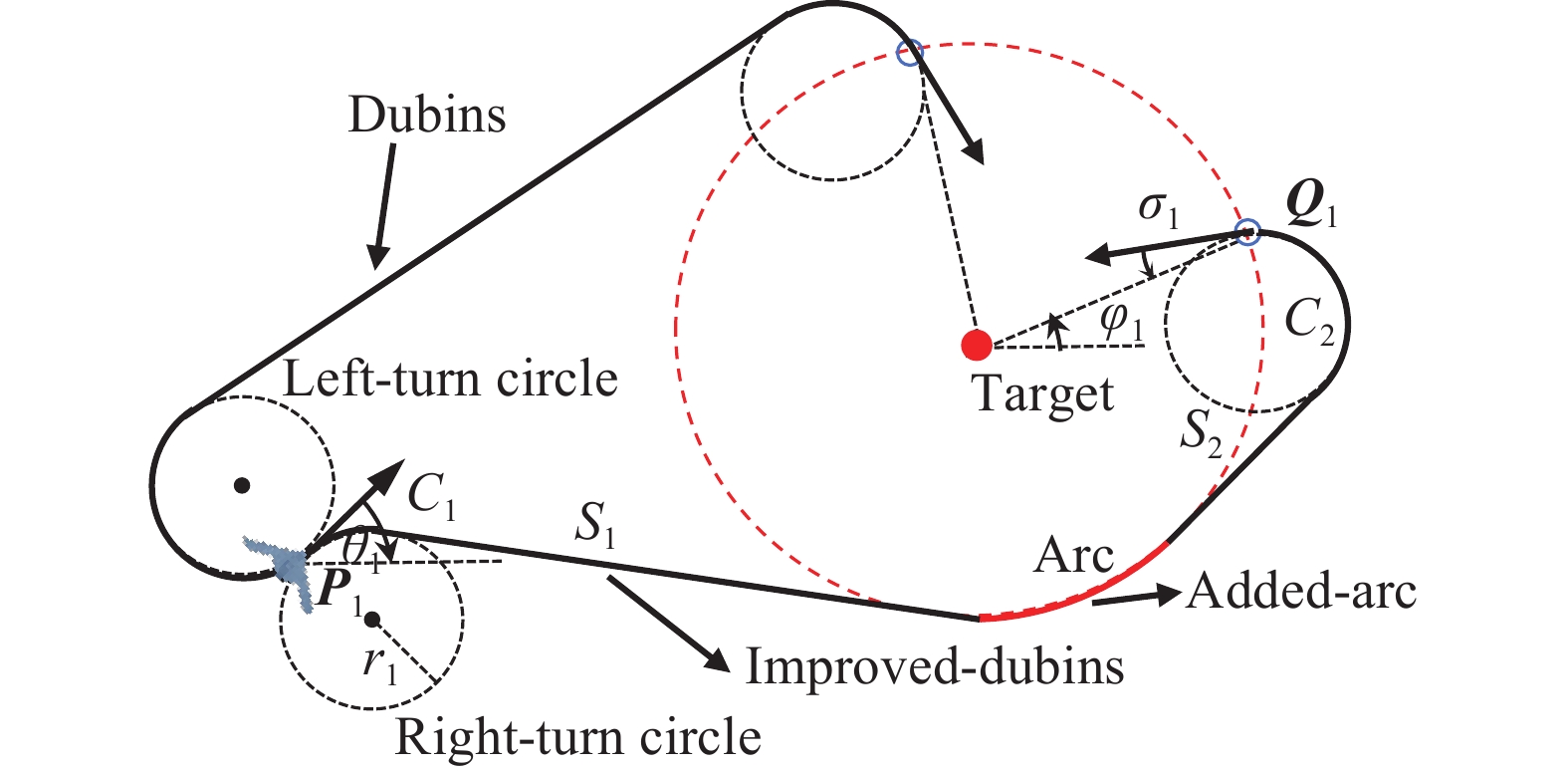
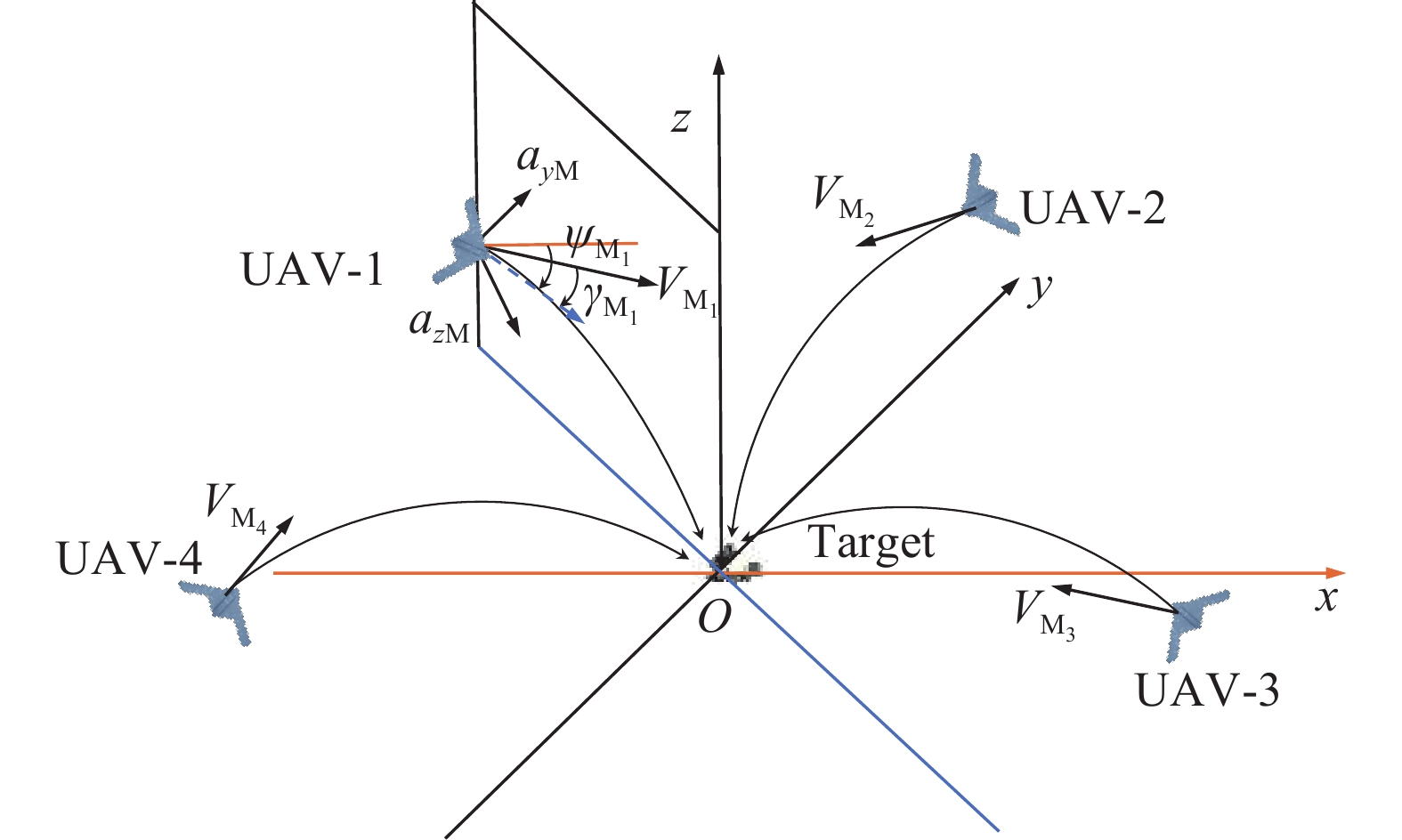
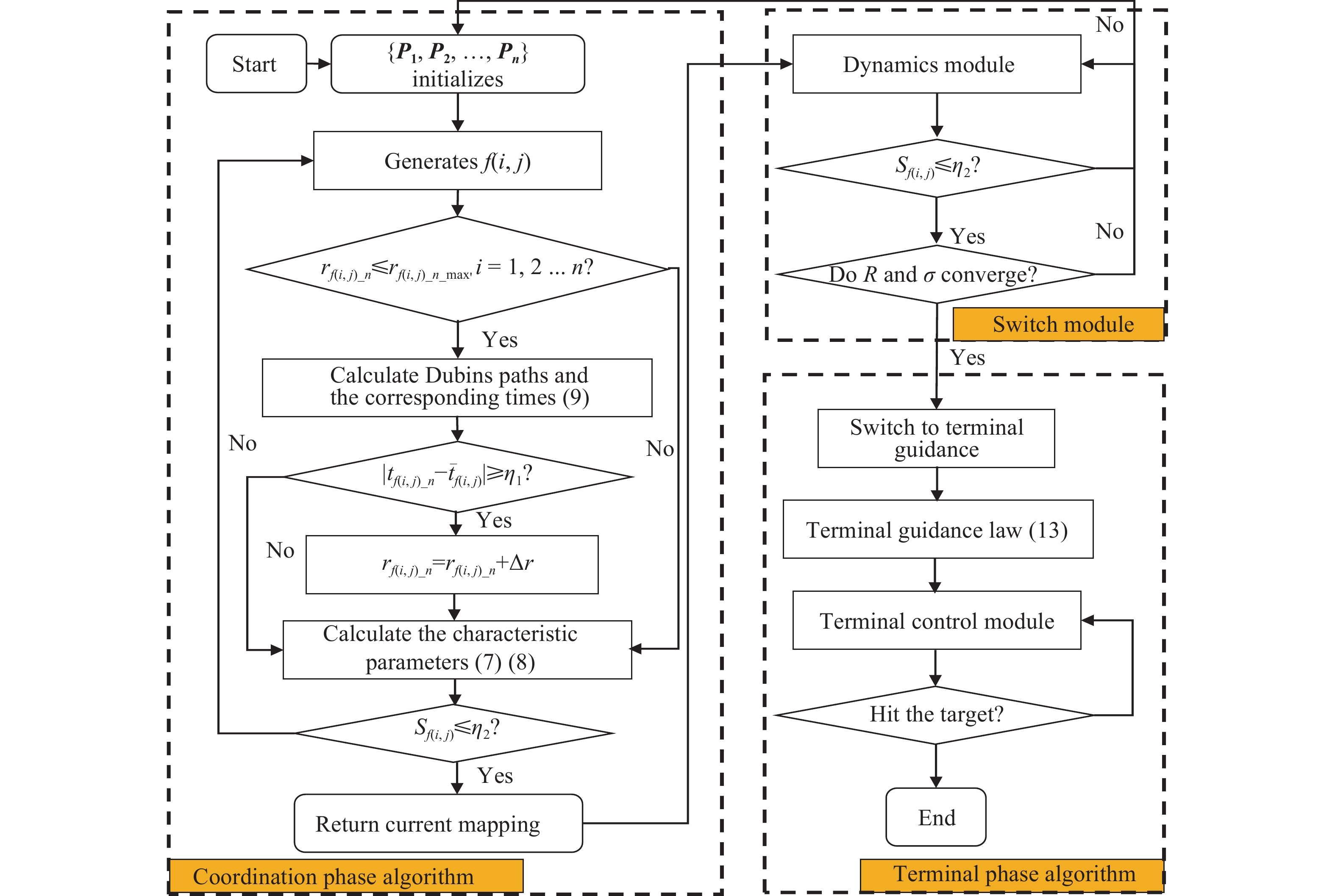
摘要: 根據多無人機協同打擊的作戰特點和要求，提出了一種通用性集群時空協同打擊制導控制方案。該方案分析了比例導引律(Proportional navigation law, PN)在滿足特定協調變量一致時具有下彈道唯一的特性，以此為基礎，通過選取協調變量，將制導段分為協調段和末制導段。協調段的航跡控制采用改進Dubins方法，實現了協調變量的時空同步收斂；末制導段將三維空間制導解耦為縱向平面與側向平面的制導，基于同系數比例導引實現集群攻擊時間一致。分段航跡控制實現了集群在考慮目標防御射界約束下的時空協同。數值仿真和實際飛行試驗結果表明，該方案具有實時的在線規劃能力，能夠實現大規模集群時空協同下的全向飽和攻擊，打擊時間精度和空間精度較高。Abstract: With the gradual establishment of regional cooperative air defense systems by the world’s military powers, the success rate of a single-aircraft penetration operation is greatly reduced, and the concept of many-to-one cooperative operation has been widely valued. As a new type of lethal aerial weapon, suicide unmanned aerial vehicles (UAVs) have played an important role in many local wars recently. Compared with traditional missiles, suicide UAVs can hover in a combat area for a long time, waiting for potential targets. Moreover, a suicide UAV cannot be easily detected via an early warning system and can approach targets covertly. Further, the manufacturing cost of a suicide UAV is low, and it can form a large-scale swarm for a surprise attack. Therefore, in the foreseeable future, a multi-UAV cooperative attack is likely to subvert existing combat styles. According to the operational characteristics and requirements of multi-UAV cooperative attacks, a general guidance scheme for the cooperative attack of multi-UAVs is proposed. Based on the theory that proportional navigation law has trajectory uniqueness under specific variable constraints, the guidance phase is divided into coordination and terminal phases by selecting coordinated variables. The improved Dubins method is used in the track control of the coordination phase to realize the space–time synchronous convergence of coordination variables. The 3D space guidance is decoupled into longitudinal- and lateral-plane guidance in the terminal phase, and the impact time of the swarm is consistent based on the proportional guidance with the same coefficient. A track segment control realizes the space–time cooperation of the swarm considering the target defense range constraint. Numerical simulation and actual flight test results show that the scheme has real-time online planning ability, can realize an omnidirectional saturation attack under the space–time cooperation of a large-scale UAV swarm, and has high impact time and space precision.
-
Key words:
- multi-UAVs /
- cooperative attack /
- space–time coordination /
- coordinated variables /
- segmented track /
- flight experiment
-
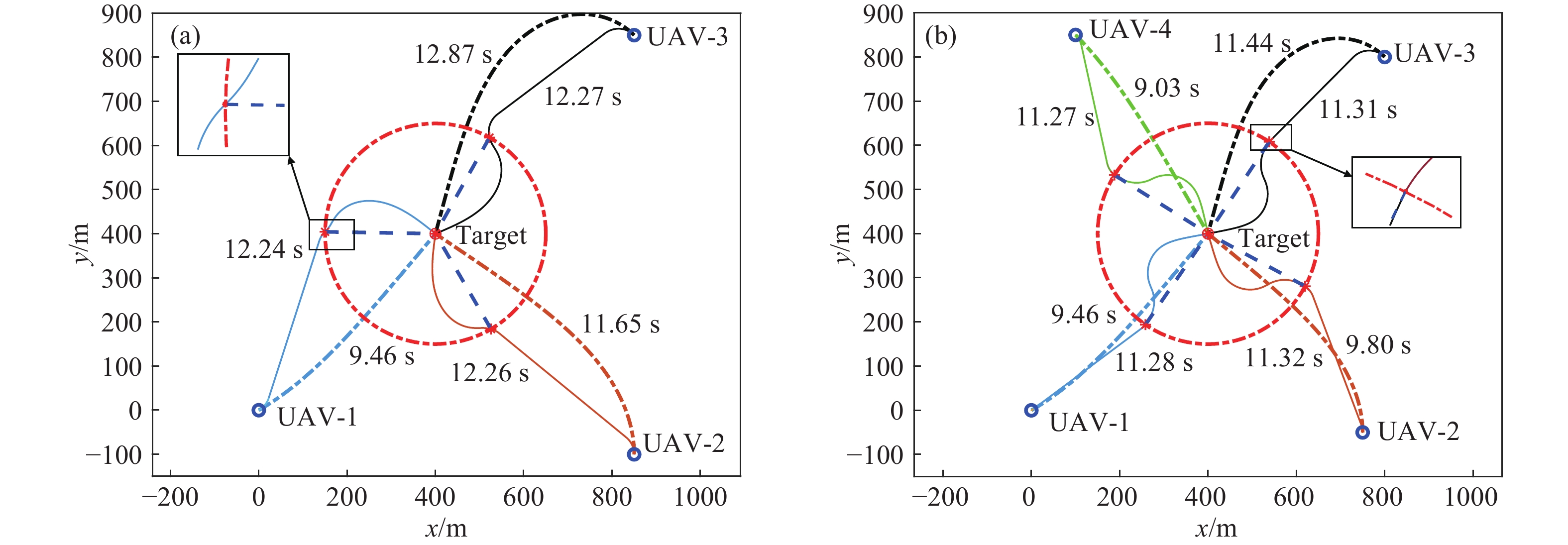
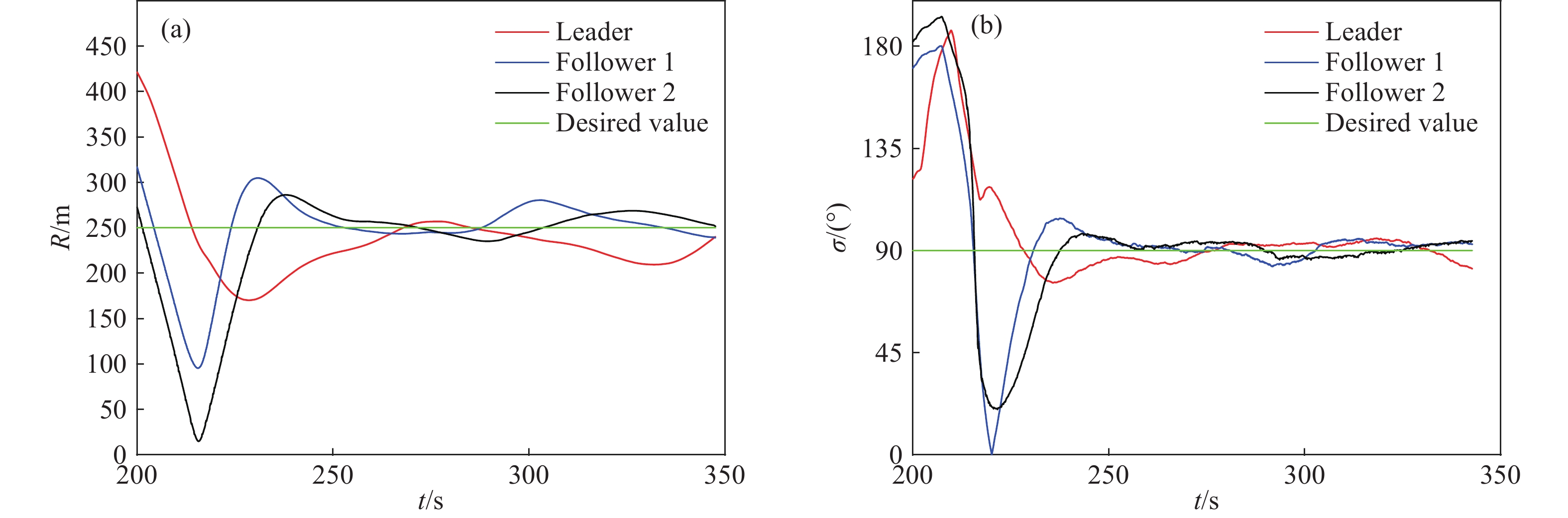
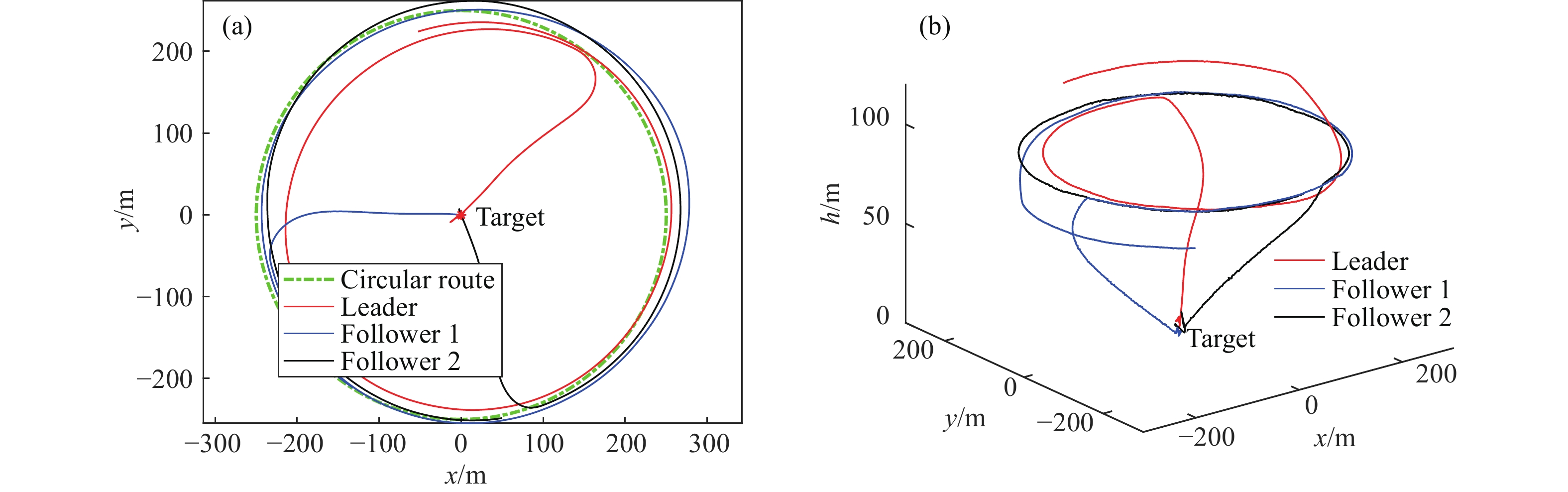
圖 6 仿真結果. (a) 三機
$ {\sigma ^ * }{\text{ = 4}}{{\text{5}}^ \circ } $ 分段制導仿真結果; (b) 四機${\sigma ^ * } = {0^ \circ }$ 分段制導仿真結果Figure 6. Simulation results: (a) 3-UAVs segmented guidance when
${\sigma ^ * }{\text{ = 4}}{{\text{5}}^ \circ } $ ; (b) 4-UAVs segmented guidance when$ {\sigma ^ * } = {0^ \circ } $ 
圖 7 系統組成. (a) 協同打擊驗證系統架構; (b) 模型機設備情況
Figure 7. System construction: (a) architecture of the collaborative attack verification system; (b) installation of the model UAV
圖 9 協調段飛行數據. (a)協調段二維航跡; (b)僚機相對相位變化
Figure 9. Flight data of the coordination phase: (a) 2D track of the coordination phase; (b) relative phase change of wing UAVs
圖 10 協調變量. (a) 二維距離R變化; (b) 速度前置角
$\sigma $ 變化Figure 10. Coordinated variables: (a) change process of the 2D distance; (b) change process of the velocity leading angle
圖 11 末制導段航跡. (a)末制導段二維航跡; (b) 末制導段三維航跡
Figure 11. Track of terminal phase: (a) 2D track; (b) 3D track
圖 12 實拍圖像. (a)打擊前一時刻各機位置; (b) 打擊瞬間圖像
Figure 12. Real images: (a) positions of UAVs at the moment before striking; (b) images of an instant hit
表 1 飛行相關點的相對坐標
Table 1. Relative coordinates of flight-related points
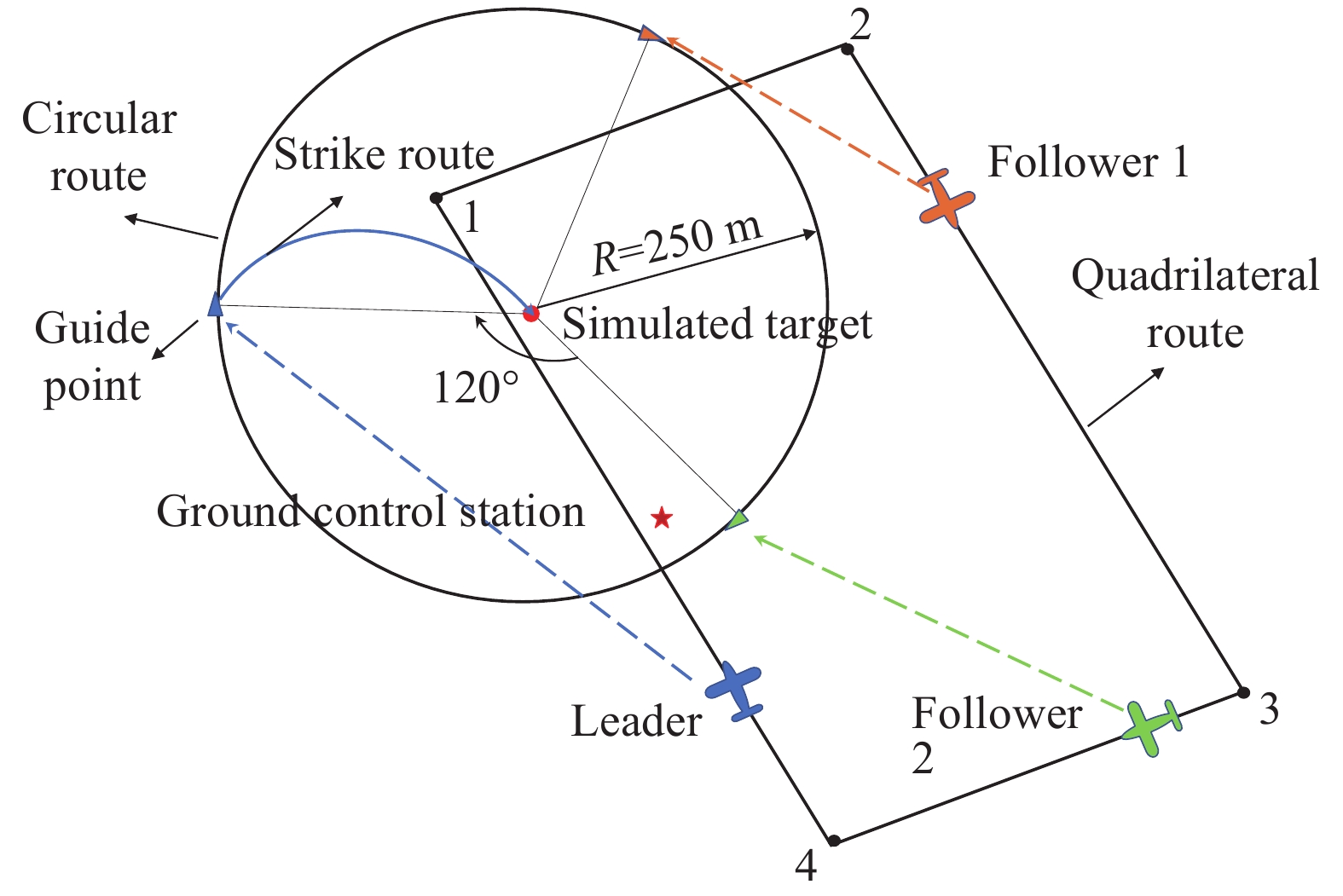
Flight-related points East/m North/m Height/m Ground control station 0 0 0 Attack point ?88 165 0 Waypoint 1 ?115 221 90 Waypoint 2 121 257 90 Waypoint 3 334 ?94 90 Waypoint 4 88 ?156 90 
下載: 導出CSV
表 2 打擊發起時刻協調變量偏差
Table 2. Coordinate variables deviation at the attack initiation time
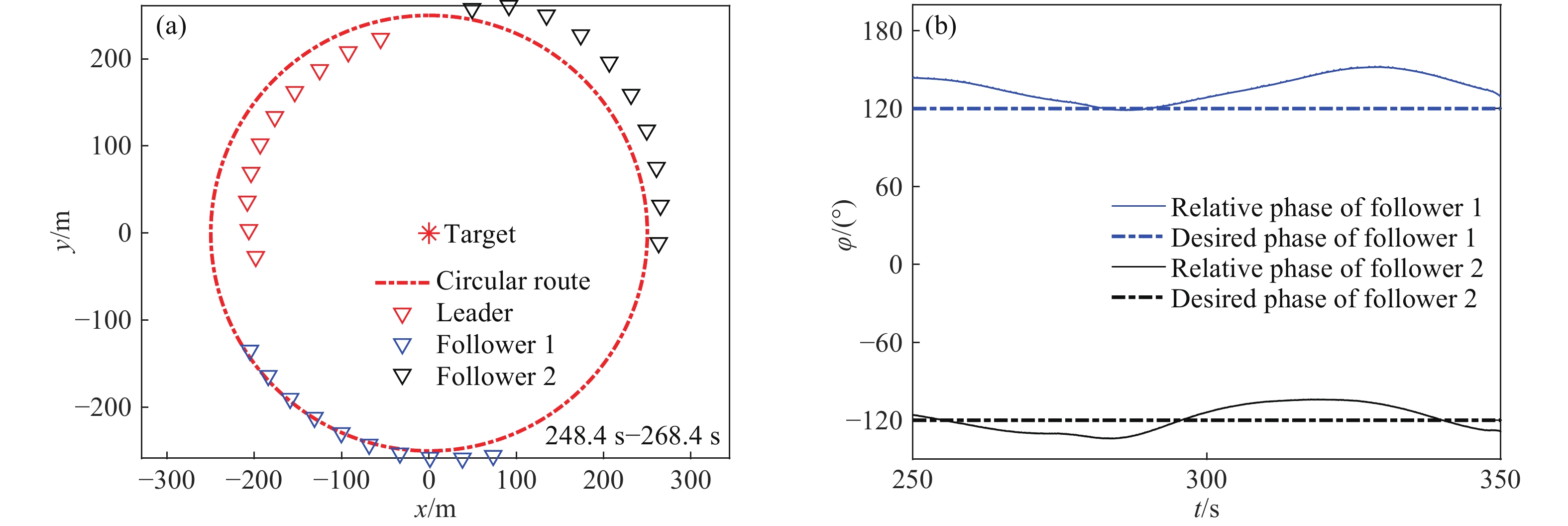
Number Deviation of $\varphi $/(°) Deviation of $R$/m Deviation of $\sigma $/(°) Leader 0 ?10.2 ?8.5 Wing 1 4.5 ?10.5 4.8 Wing 2 ?5.2 2.5 5.2
下載: 導出CSV
表 3 末制導段飛行時間和空間偏差
Table 3. Flight time and space deviation of the terminal phase
Number Flight time of terminal phase /s Deviation of 2D distance/m Deviation of
height/mLeader 11.9 0.28 0.27 Wing 1 10.6 0.23 0.25 Wing 2 11.3 0.06 0.31
下載: 導出CSV
www.77susu.com<span id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> <span id="fpn9h"><noframes id="fpn9h"> <th id="fpn9h"></th> <strike id="fpn9h"><noframes id="fpn9h"><strike id="fpn9h"></strike> <th id="fpn9h"><noframes id="fpn9h"> <span id="fpn9h"><video id="fpn9h"></video></span> <ruby id="fpn9h"></ruby> <strike id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> -
參考文獻
[1] Kim H G, Kim H J. Backstepping-based impact time control guidance law for missiles with reduced seeker field-of-view. IEEE Trans Aerosp Electron Syst, 2019, 55(1): 82 doi: 10.1109/TAES.2018.2848319 [2] Zeng J, Dou L H, Xin B. A joint mid-course and terminal course cooperative guidance law for multi-missile salvo attack. Chin J Aeronaut, 2018, 31(6): 1311 doi: 10.1016/j.cja.2018.03.016 [3] Zhen Z Y, Xing D J, Gao C. Cooperative search-attack mission planning for multi-UAV based on intelligent self-organized algorithm. Aerosp Sci Technol, 2018, 76: 402 doi: 10.1016/j.ast.2018.01.035 [4] Duan H B, Zhao J X, Deng Y M, et al. Dynamic discrete pigeon-inspired optimization for multi-UAV cooperative search-attack mission planning. IEEE Trans Aerosp Electron Syst, 2021, 57(1): 706 doi: 10.1109/TAES.2020.3029624 [5] Liu X, Liu L, Wang Y J. Minimum time state consensus for cooperative attack of multi-missile systems. Aerosp Sci Technol, 2017, 69: 87 doi: 10.1016/j.ast.2017.06.016 [6] He S M, Kim M, Song T, et al. Three-dimensional salvo attack guidance considering communication delay. Aerosp Sci Technol, 2018, 73: 1 doi: 10.1016/j.ast.2017.11.019 [7] Kang S, Wang J N, Li G, et al. Optimal cooperative guidance law for salvo attack: An MPC-based consensus perspective. IEEE Trans Aerosp Electron Syst, 2018, 54(5): 2397 doi: 10.1109/TAES.2018.2816880 [8] Peng Z H, Sun L, Chen J. Online path planning for UAV low-altitude penetration based on an improved differential evolution algorithm. J Univ Sci Technol Beijing, 2012, 34(1): 96彭志紅, 孫琳, 陳杰. 基于改進差分進化算法的無人機在線低空突防航跡規劃. 北京科技大學學報, 2012, 34(1):96 [9] Kim C Y, Ra W S, Whang I H. Time-to-go rational function biased PN guidance law for precise impact angle // 2017 17th International Conference on Control, Automation and Systems (ICCAS). Jeju, 2017: 1804 [10] Chen X T, Wang J Z. Nonsingular sliding-mode control for field-of-view constrained impact time guidance. J Guid Control Dyn, 2018, 41(5): 1214 doi: 10.2514/1.G003146 [11] Erer K S, Tekin R. Impact time and angle control based on constrained optimal solutions. J Guid Control Dyn, 2016, 39(10): 2448 doi: 10.2514/1.G000414 [12] Hou Z W, Liu L, Wang Y J. Time-to-go estimation for terminal sliding mode based impact angle constrained guidance. Aerosp Sci Technol, 2017, 71: 685 doi: 10.1016/j.ast.2017.10.016 [13] Zhao J B, Yang S X. Integrated cooperative guidance framework and cooperative guidance law for multi-missile. Chin J Aeronaut, 2018, 31(3): 546 doi: 10.1016/j.cja.2017.12.013 [14] Xu Q Q, Ge J Q, Yang T. Multiple missiles cooperative guidance based on proportional navigation guidance // 2020 Chinese Control and Decision Conference (CCDC). Hefei, 2020: 4423 [15] Song J H, Song S M, Xu S L. Three-dimensional cooperative guidance law for multiple missiles with finite-time convergence. Aerosp Sci Technol, 2017, 67: 193 doi: 10.1016/j.ast.2017.04.007 [16] Kim H G, Cho D, Kim H J. Sliding mode guidance law for impact time control without explicit time-to-go estimation. IEEE Trans Aerosp Electron Syst, 2019, 55(1): 236 doi: 10.1109/TAES.2018.2850208 [17] Zhu J W, Su D L, Xie Y, et al. Impact time and angle control guidance independent of time-to-go prediction. Aerosp Sci Technol, 2019, 86: 818 doi: 10.1016/j.ast.2019.01.047 [18] Zhu J W, Yang Y P, Zhang W A, et al. Cooperative attack tolerant tracking control for multi-agent system with a resilient switching scheme. Neurocomputing, 2020, 409: 372 doi: 10.1016/j.neucom.2020.06.087 [19] Zhao J B, Yang S X. Review of multi-missile cooperative guidance. Acta Aeronaut et Astronaut Sin, 2017, 38(1): 020256趙建博, 楊樹興. 多導彈協同制導研究綜述. 航空學報, 2017, 38(1):020256 [20] Lü T, Lü Y Y, Li C J, et al. Time-cooperative guidance law for multiple missiles with spatial cooperation. Acta Aeronaut et Astronaut Sin, 2018, 39(10): 322115呂騰, 呂躍勇, 李傳江, 等. 帶空間協同的多導彈時間協同制導律. 航空學報, 2018, 39(10):322115 [21] Ji H B, Liu X D, Song Z Y, et al. Time-varying sliding mode guidance scheme for maneuvering target interception with impact angle constraint. J Frankl Inst, 2018, 355(18): 9192 doi: 10.1016/j.jfranklin.2017.01.036 [22] He S M, Wang W, Wang J. Three-dimensional impact angle guidance laws based on model predictive control and sliding mode disturbance observer. J Dyn Syst Meas Control, 2016, 138(8): 081006 doi: 10.1115/1.4033272 [23] Liu B J, Hou M S, Yu Y, et al. Three-dimensional impact angle control guidance with field-of-view constraint. Aerosp Sci Technol, 2020, 105: 106014 doi: 10.1016/j.ast.2020.106014 [24] Shaferman V, Shima T. Cooperative differential games guidance laws for imposing a relative intercept angle. J Guid Control Dyn, 2017, 40(10): 2465 doi: 10.2514/1.G002594 [25] Wei X Q, Yang J Y, Fan X R. Design of distributed guidance laws for multiple unmanned aerial vehicles cooperative attack of a moving target based on reducing surrounding area. Trans Inst Meas Control, 2020, 42(12): 2155 doi: 10.1177/0142331220908683 [26] Lee C H, Tsourdos A. Cooperative control for multiple interceptors to maximize collateral damage. IFAC-PapersOnLine, 2018, 51(12): 56 doi: 10.1016/j.ifacol.2018.07.088 [27] Yang Z. Research on Multi-Constrainted Terminal Guidance Laws and Target State Estimation Methods [Dissertation]. Beijing: Beijing Institute of Technology, 2017楊哲. 多約束末制導律與目標狀態估計方法研究[學位論文]. 北京: 北京理工大學, 2017 [28] Xin H B, Chen Q Y, Wang Y J, et al. A path planning and guidance method for multi-UAVs coordinated strike with time-space constraints // 2020 12th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC). Hangzhou, 2020: 193 [29] Xu C, Huang D Q, Kong F Q. Small UAV passive target localization approach and accuracy analysis. Chin J Sci Instrum, 2015, 36(5): 1115徐誠, 黃大慶, 孔繁鏘. 一種小型無人機無源目標定位方法及精度分析. 儀器儀表學報, 2015, 36(5):1115 -
點擊查看大圖
計量
- 文章訪問數: 492
- HTML全文瀏覽量: 282
- PDF下載量: 106
- 被引次數: 0
