Creep property and damage constitutive model of dioritic porphyrite under cyclic loading-unloading
-
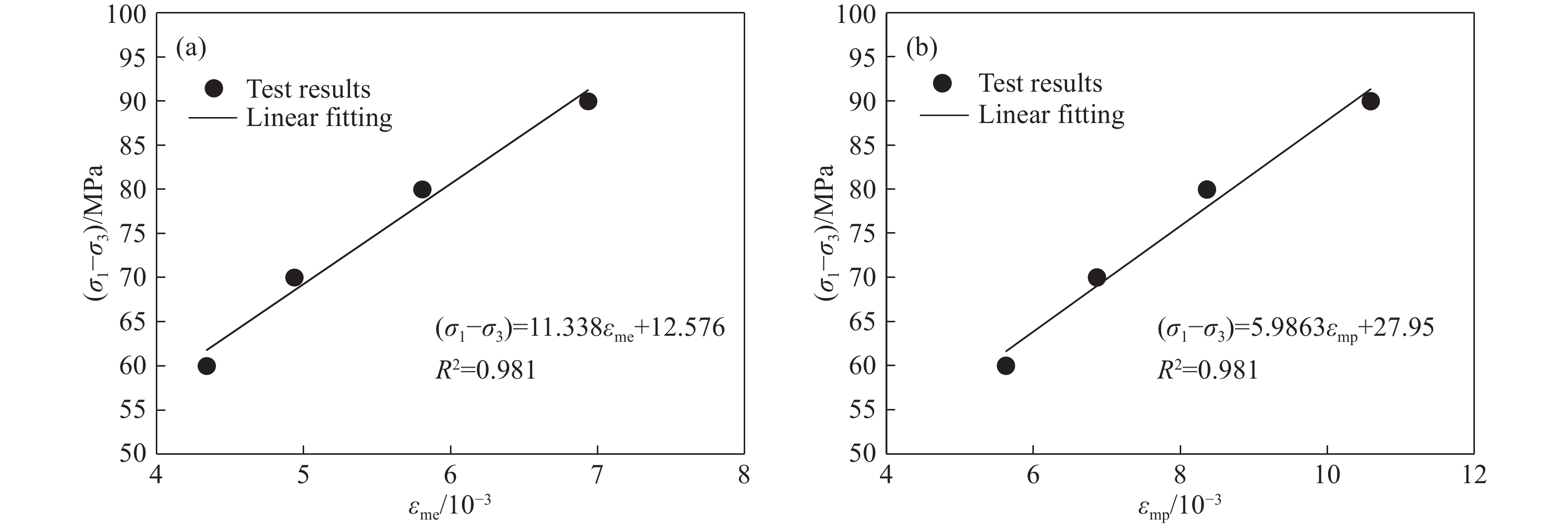
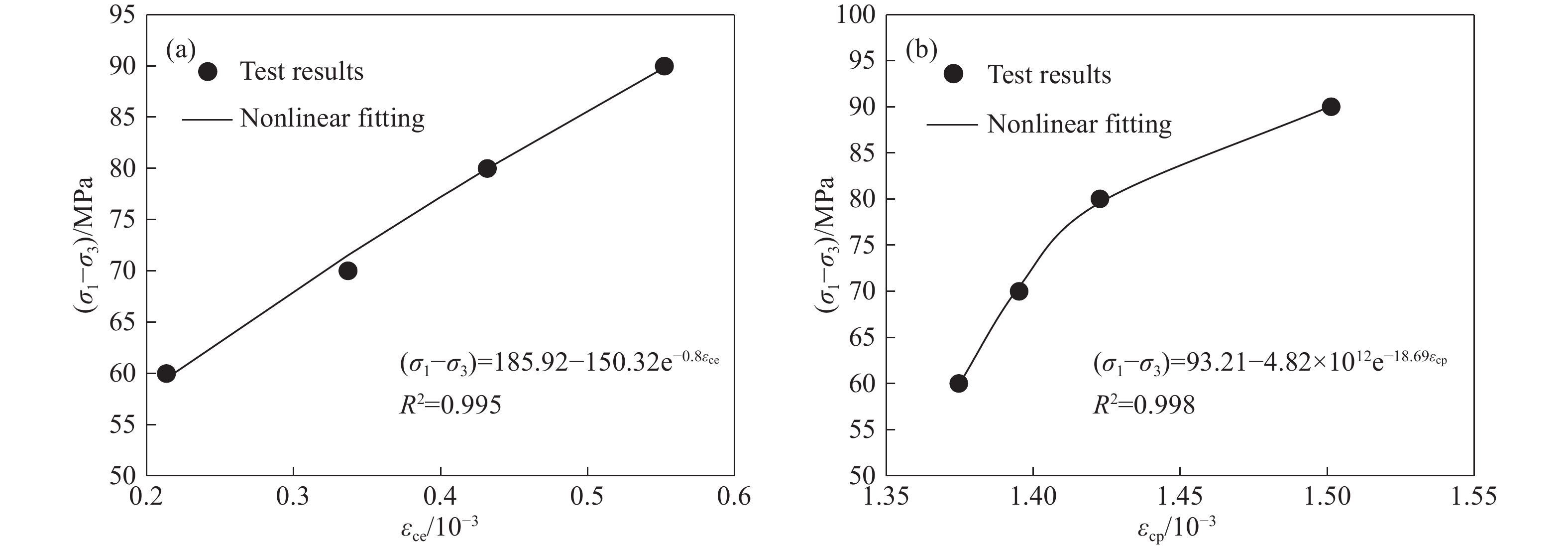
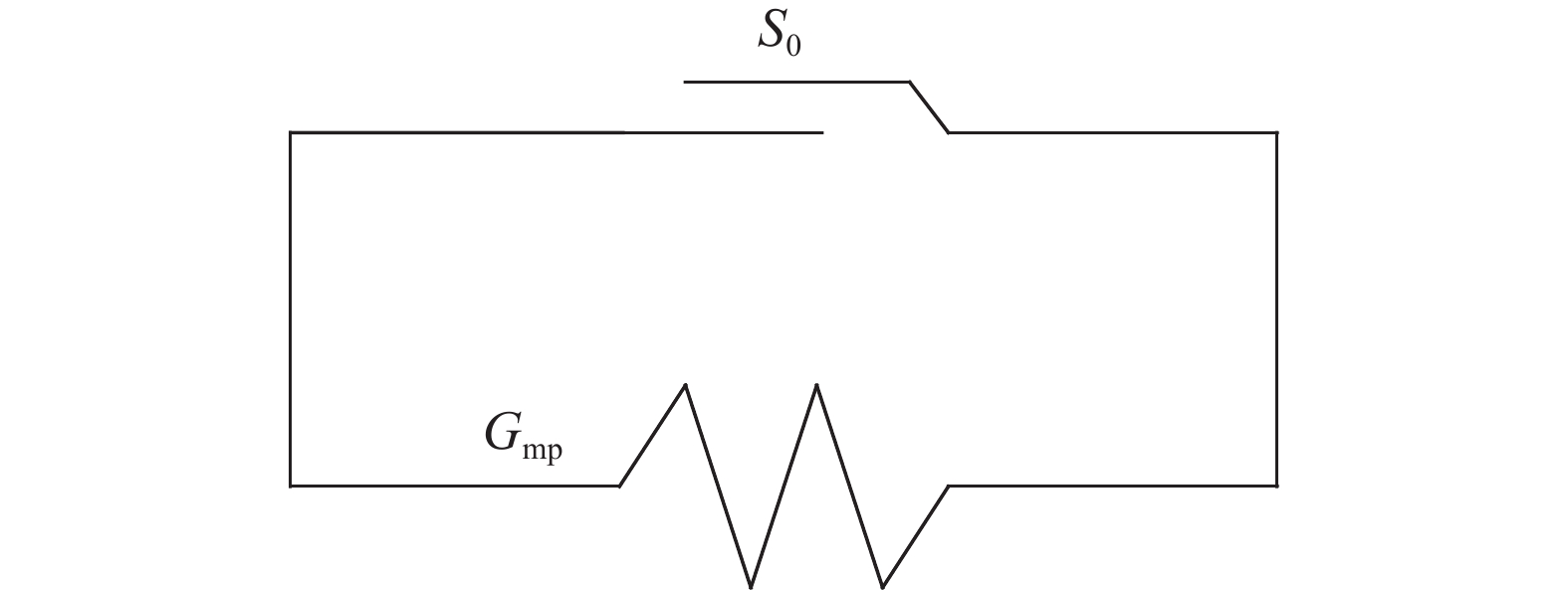
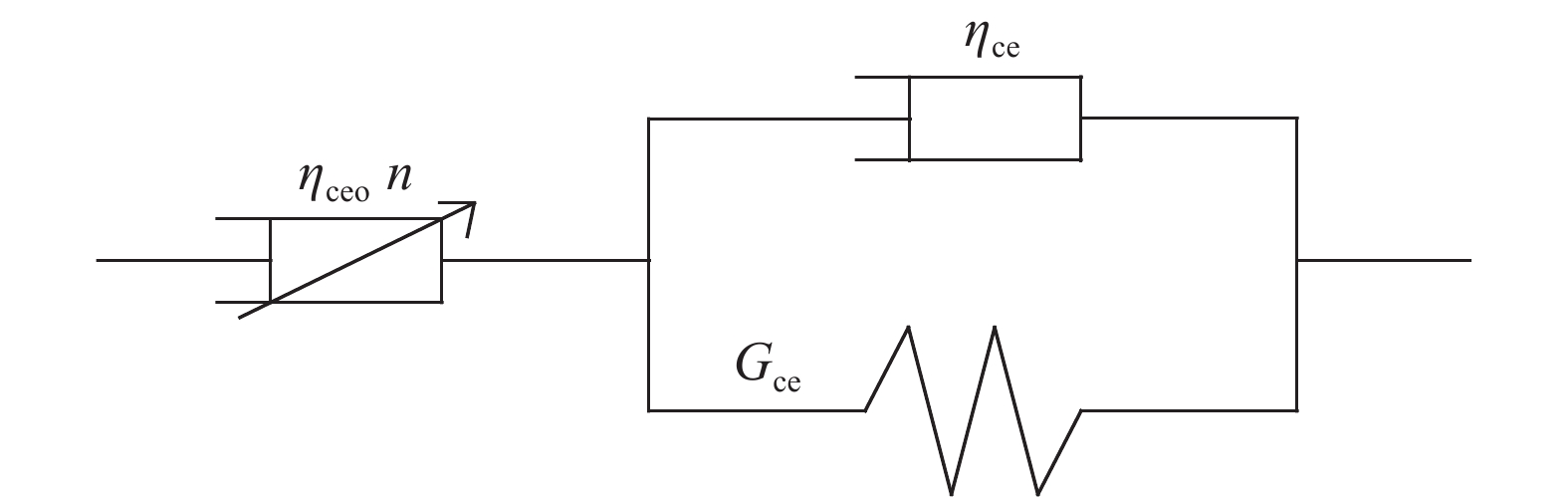
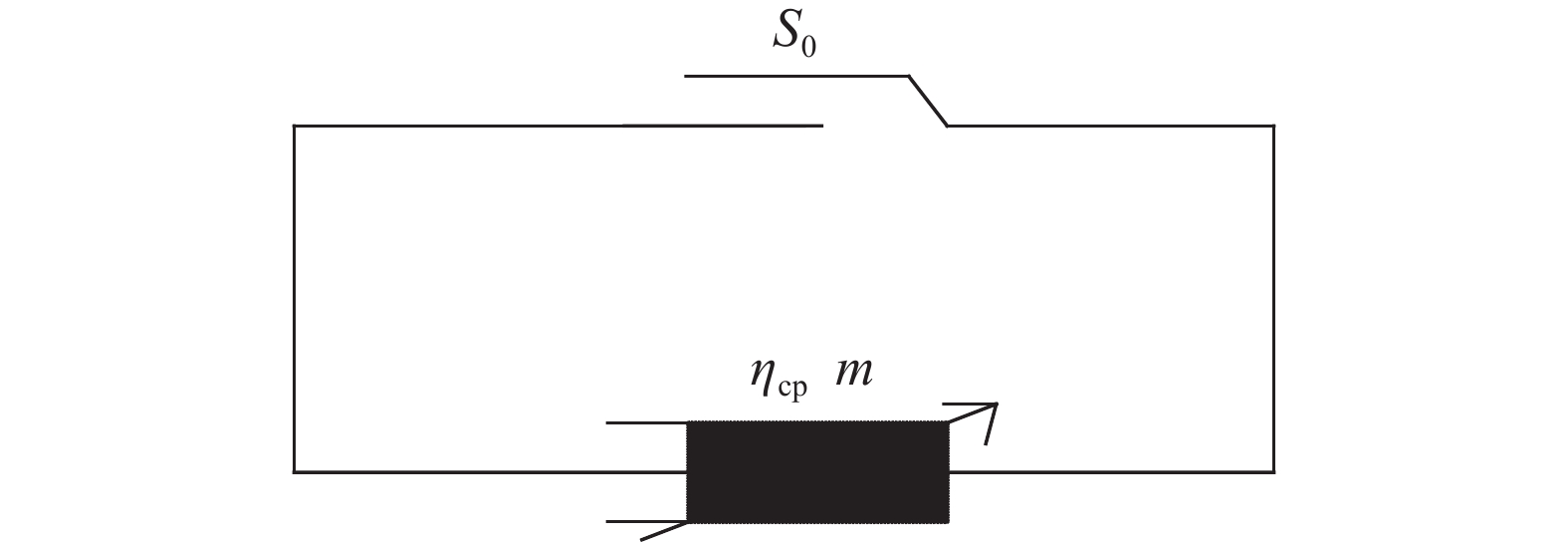
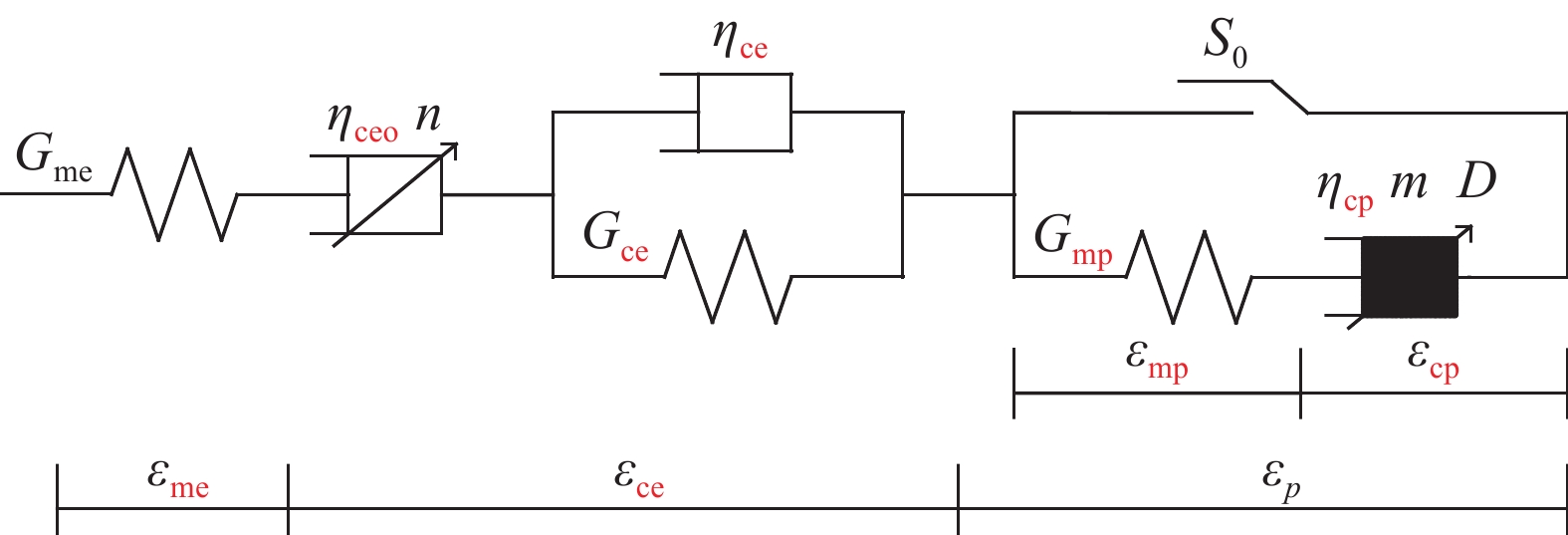
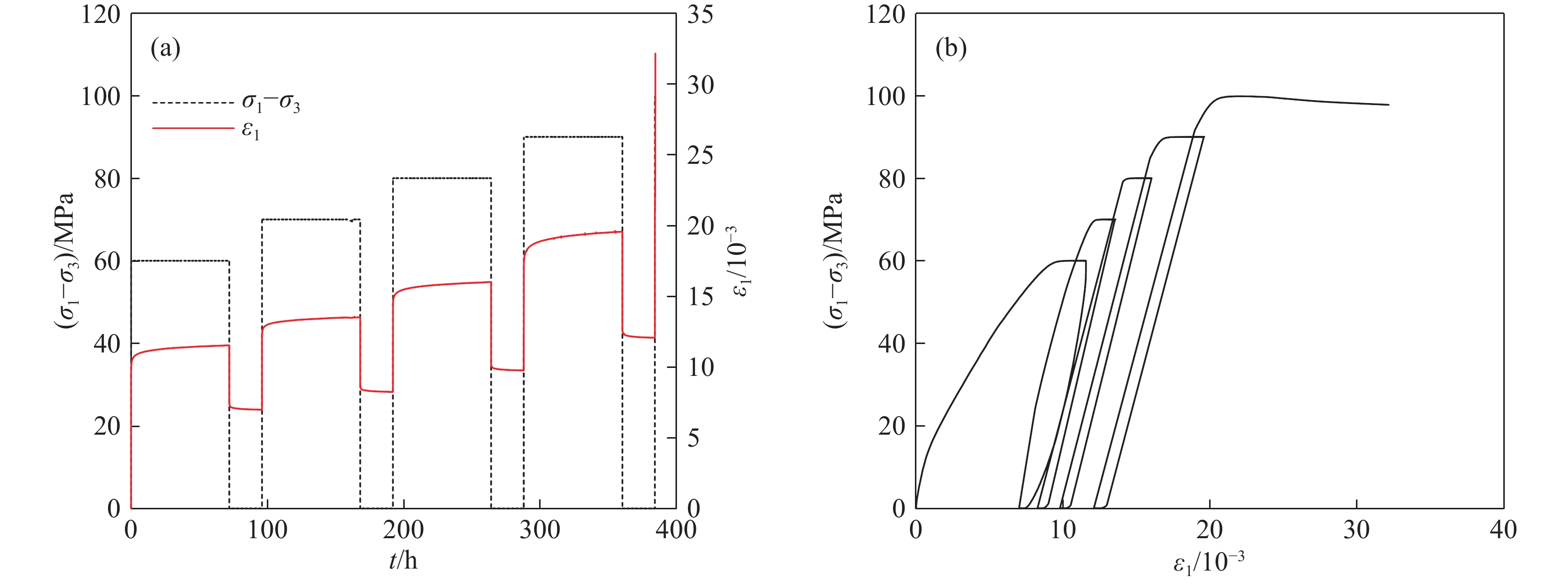
摘要: 分級加載壓縮蠕變試驗未能充分考慮穩定蠕變中的黏塑性應變，故采用三軸循環加卸載壓縮蠕變試驗來實現巖石的黏彈、塑性應變分離，從而使巖石黏彈、塑性應變在巖石蠕變的各個階段得以充分考慮。以某水電站閃長玢巖為例，探討該類巖石蠕變特性。在破壞前，巖石的瞬時彈性應變以及瞬時塑性應變隨著偏應力逐級增大呈線性增長；隨著偏應力的增加，黏彈性應變和黏塑性應變呈非線性增長。引入一個分數階Abel黏壺與Kelvin模型串聯形成新型黏彈性模型；用分數階Abel黏壺代替傳統的黏塑性模型中的線性牛頓體并基于損傷建立黏塑性損傷模型。然后將新型黏彈性模型和黏塑性損傷模型與瞬時彈性模型和瞬時塑性模型串聯組成一個新的巖石蠕變損傷模型。最后將該模型與巖石蠕變曲線進行擬合，從而證明該模型的適用性。Abstract: The hierarchical loading compression creep test fails to fully consider the viscoplastic strain in a stable creep. Thus, the triaxial cyclic loading compression creep test is adopted to realize the separation of viscoelastic and viscoplastic strain to fully consider the two strains in each stage of the creep. With the development of hydropower project construction in China being moved towards the mountain valley, the geological conditions and engineering environment faced by geotechnical engineering become more complex. Moreover, in the process of geotechnical engineering design, engineering construction, and safe operation, the effect of the rheological, mechanical properties of rock becomes more difficult to ignore. This engineering problem is becoming more significant for the staff involved. Therefore, rheological, mechanical properties of rock have become a very important research content. This study took the diorite porphyry of one hydropower station as an example to discuss the creep characteristics of this type of rock. Before the failure, the instantaneous elastic strain and instantaneous plastic strain increase linearly as the deviator stress gradually increases. With increased deviator stress, the viscoelastic strain and viscoplastic strain exhibit a nonlinear increase. The fractional Abel viscous pot and Kelvin model were introduced to form a new viscoelastic model. The fractional Abel viscous pot was used to replace the linear Newtonian fluid in the traditional viscoplastic model, and a viscoplastic damage model was established based on the damage variables. The new viscoelastic plastic model and viscoplastic damage model were then connected in series with the transient elastic model and transient plastic model to form a new rock creep damage model. Finally, the model is fitted with the rock creep curve to prove the applicability of the model.
-
圖 1 閃長玢巖三軸壓縮蠕變試驗結果。（a）應變、應力?時間曲線；（b）應力?應變曲線
Figure 1. Triaxial compression creep test results of diorite porphyrite: (a) strain and stress vs time curves; (b) stress?strain curve
圖 2 不同偏應力加載閃長玢巖的瞬時應變。（a）瞬時彈性應變；（b）瞬時塑性應變
Figure 2. Instantaneous strain of diorite porphyry under different deviatoric stress loading: (a) instantaneous elastic strain; (b) transient plastic strain
圖 3 不同偏應力加載時閃長玢巖的蠕變應變。（a）黏彈性應變；（b）黏塑性應變
Figure 3. Creep strain of diorite porphyry under different deviatoric stress loading: (a) viscoelastic strain; (b) viscoplastic strain
圖 6 90 MPa 為例示意圖。（a）擬合結果對比；（b）黏彈、塑性應變分離結果
Figure 6. 90 MPa schematic diagram: (a) comparison of fitting results; (b) results of viscoelastic and plastic strain separation
圖 9 試驗與模型擬合結果。（a）穩態流變擬合；（b）加速流變擬合
Figure 9. Test and model fitting results: (a) steady state rheological fitting; (b) accelerated rheological fitting
表 1 閃長玢巖三軸循環加卸載蠕變試驗黏彈塑性應變分析
Table 1. Viscoelastic strain analysis of diorite porphyrite triaxial cyclic loading and unloading creep test
σa/MPa σb/MPa εm/ 10?3 εme/ 10?3 εmp/ 10?3 εc/ 10?3 εce/ 10?3 εcp/ 10?3 εp/ 10?3 60 0 9.967 4.342 5.625 1.588 0.213 1.375 7.000 70 0 11.799 4.937 6.862 1.732 0.337 1.395 8.257 80 0 14.169 5.807 8.361 1.854 0.432 1.423 9.784 90 0 17.526 6.937 10.589 2.053 0.552 1.501 12.091 100 0 20.382 4.761 
下載: 導出CSV
表 2 Kelvin模型與改進Kelvin模型擬合參數
Table 2. Fitting parameters of the Kelvin model and improved Kelvin model
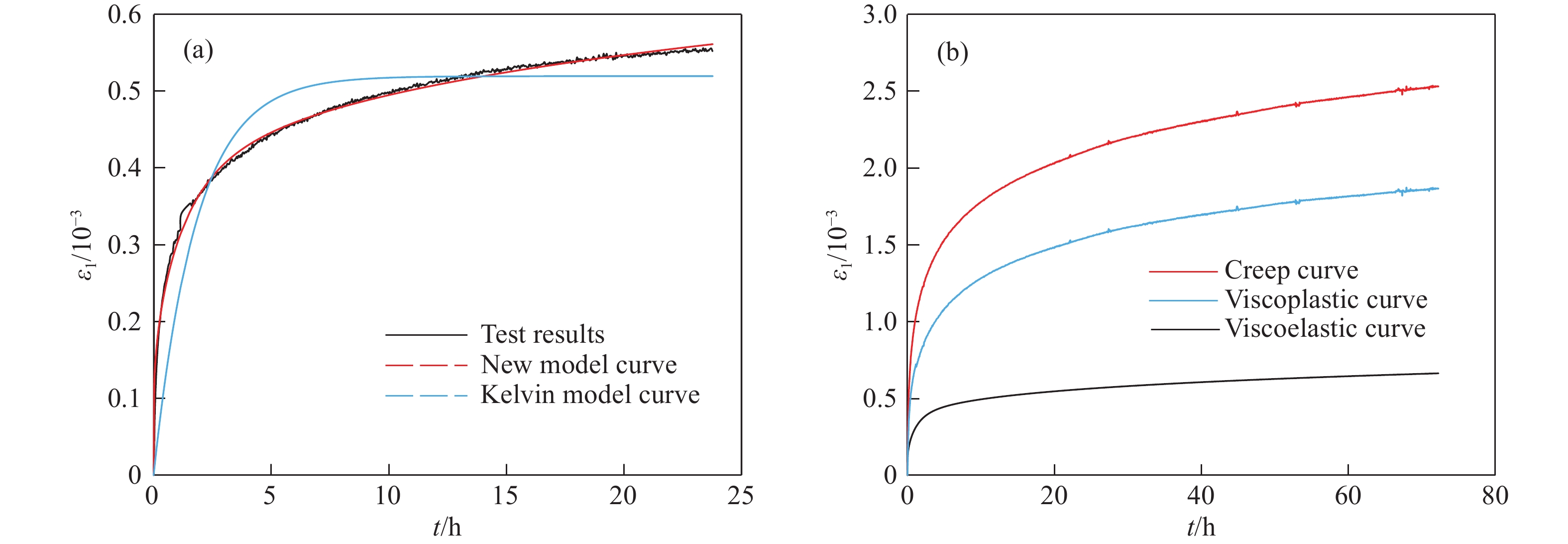
(σ1?σ3) / MPa Viscoelastic model ηceo/ GPa?h Gce/ GPa ηce/ GPa?h n R2 60 Kelvin model — 99.57 488.12 — 0.974 New viscoelastic model 666.67 240.96 848.46 0.430 0.998 70 Kelvin model — 74.75 187.54 — 0.864 New viscoelastic model 238.10 256.41 398.15 0.263 0.996 80 Kelvin model — 65.16 112.93 — 0.808 New viscoelastic model 175.44 222.22 254.26 0.212 0.996 90 Kelvin model — 57.75 104.06 — 0.784 New viscoelastic model 140.85 225.56 302.36 0.194 0.995
下載: 導出CSV
表 3 蠕變模型參數
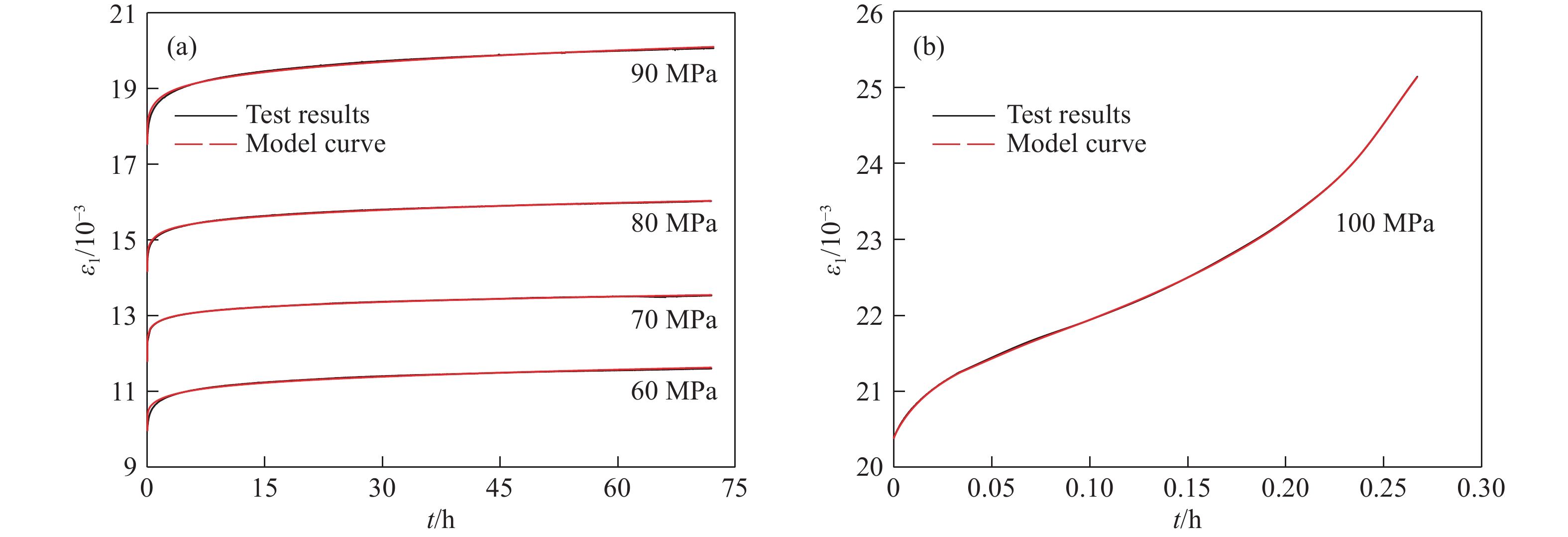
Table 3. Creep model parameters
（σ1?σ3）/
MPaA B C E n m b tp R2 60 0.03 0.083 0.284 0.655 0.43 0.156 — — 0.991 70 0.098 0.091 0.644 0.799 0.263 0.106 — — 0.997 80 0.152 0.12 0.874 0.628 0.212 0.159 — — 0.996 90 0.213 0.133 0.746 0.722 0.194 0.206 — — 0.994 100 0.096 0.482 60.35 3.657 0.665 0.677 0.59 0.345 0.999
下載: 導出CSV
www.77susu.com<span id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> <span id="fpn9h"><noframes id="fpn9h"> <th id="fpn9h"></th> <strike id="fpn9h"><noframes id="fpn9h"><strike id="fpn9h"></strike> <th id="fpn9h"><noframes id="fpn9h"> <span id="fpn9h"><video id="fpn9h"></video></span> <ruby id="fpn9h"></ruby> <strike id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> -
參考文獻
[1] Cai M F, He M C, Liu D Y. Rock Mechanics and Engineering. 2nd Ed. Beijing: Science Press, 2019蔡美峰, 何滿潮, 劉東燕. 巖石力學與工程. 2版 北京: 科學出版社, 2019 [2] Sun J. Rheological Behavior of Geomaterials and its Engineering Applications. Beijing: China Architecture and Building Press, 1999孫鈞. 巖土材料流變及其工程應用. 北京: 中國建筑工業出版社, 1999 [3] Cruden D M. Single-increment creep experiments on rock under uniaxial compression. Int J Rock Mech Min Sci Geomech Abstr, 1971, 8(2): 127 doi: 10.1016/0148-9062(71)90004-0 [4] Li Y S. Creep and relaxation of 4 kinds of rock under uniaxial cimpression tests. Chin J Rock Mech Eng, 1995, 14(1): 39李永盛. 單軸壓縮條件下四種巖石的蠕變和松弛試驗研究. 巖石力學與工程學報, 1995, 14(1):39 [5] Zhao X J, Chen B R, Zhao H B, et al. Laboratory creep tests for time-dependent properties of a marble in Jinping II hydropower station. J Rock Mech Geotech Eng, 2012(2): 168 [6] Xu P, Yang S Q. Study of visco-elasto-plastic constitutive model of coal under cyclic loading. Chin J Rock Mech Eng, 2015, 34(3): 537徐鵬, 楊圣奇. 循環加卸載下煤的黏彈塑性蠕變本構關系研究. 巖石力學與工程學報, 2015, 34(3):537 [7] Yang S Q, Hu B. Creep and long-term permeability of a red sandstone subjected to cyclic loading after thermal treatments. Rock Mech Rock Eng, 2018, 51: 2981 doi: 10.1007/s00603-018-1528-8 [8] Zhao Y L, Cao P, Wang W J, et al. Viscoelasto-plastic rheological experiment under circular increment step load and unload and nonlinear creep model of soft rocks. J Central South Univ Technol, 2009, 16(3): 488 doi: 10.1007/s11771-009-0082-7 [9] Chen Y J, Xie B X, Cao P, et al. Dimensional effect of soft rock rheology. J Univ of Sci Technol Beijing, 2008, 30(5): 468 doi: 10.3321/j.issn:1001-053X.2008.05.002陳沅江, 謝本賢, 曹平, 等. 軟巖流變的尺寸效應. 北京科技大學學報, 2008, 30(5):468 doi: 10.3321/j.issn:1001-053X.2008.05.002 [10] Koeller R C. Applications of fractional calculus to the theory of viscoelasticity. J Appl Mech, 1984, 51(2): 299 doi: 10.1115/1.3167616 [11] Yin D S, Zhang W, Cheng C, et al. Fractional time-dependent Bingham model for muddy clay. J Non Newton Fluid Mech, 2012, 187-188: 32 doi: 10.1016/j.jnnfm.2012.09.003 [12] Sha B W, Zhu Q Z, Min Z Z. Study on creep characteristics and fractional-order visco-elastoplastic model of granite. J Saf Sci Technol, 2020, 16(3): 24沙博文, 朱其志, 閔中澤. 花崗巖蠕變特性及分數階黏彈塑性模型研究. 中國安全生產科學技術, 2020, 16(3):24 [13] Zhou H W, Liu D, Lei G, et al. The creep-damage model of salt rock based on fractional derivative. Energies, 2018, 11(9): 2349 doi: 10.3390/en11092349 [14] Wu F, Chen J, Zou Q L. A nonlinear creep damage model for salt rock. Int J Damage Mech, 2019, 28(5): 758 doi: 10.1177/1056789518792649 [15] Wu F, Liu J F, Wang J. An improved Maxwell creep model for rock based on variable-order fractional derivatives. Environ Earth Sci, 2015, 73(11): 6965 doi: 10.1007/s12665-015-4137-9 [16] Su T, Zhou H W, Zhao J W, et al. A creep model of rock based on variable order fractional derivative. Chin J Rock Mech Eng, 2019, 38(7): 1355蘇騰, 周宏偉, 趙家巍, 等. 基于變階分數階導數的巖石蠕變模型. 巖石力學與工程學報, 2019, 38(7):1355 [17] Yan B Q, Ren F H, Cai M F, et al. A review of the research on physical and mechanical properties and constitutive model of rock under THMC multi-field coupling. Chin J Eng, 2020, 42(11): 1389顏丙乾, 任奮華, 蔡美峰, 等. THMC多場耦合作用下巖石物理力學性能與本構模型研究綜述. 工程科學學報, 2020, 42(11):1389 [18] Li D J, Liu X L, Han C. Variable-order fractional damage creep model based on equivalent viscoelasticity for rock. Rock Soil Mech, 2020, 41(12): 3831李德建, 劉校麟, 韓超. 基于等效黏彈性的變階分數階巖石損傷蠕變模型. 巖土力學, 2020, 41(12):3831 [19] Hu B, Yang S Q, Xu P. A nonlinear rheological damage model of hard rock. J Central South Univ, 2018, 25(7): 1665 doi: 10.1007/s11771-018-3858-9 [20] Yang S Q, Hu B. Creep and permeability evolution behavior of red sandstone containing a single fissure under a confining pressure of 30?MPa. Sci Rep, 2020, 10: 1900 doi: 10.1038/s41598-020-58595-2 [21] Wang W, Zhou X Q, Liu T G, et al. Investigation of rheological constitutive model of rocks based on viscoplastic theory. J China Three Gorges Univ Nat Sci, 2010, 32(6): 51王偉, 周先齊, 劉桃根, 等. 基于粘塑理論的巖石流變本構模型研究. 三峽大學學報(自然科學版), 2010, 32(6):51 [22] Yang S Q, Xu P, Ranjith P G. Damage model of coal under creep and triaxial compression. Int J Rock Mech Min Sci, 2015, 80: 337 doi: 10.1016/j.ijrmms.2015.10.006 [23] Zhao Y L, Wang Y X, Wang W J, et al. Modeling of non-linear rheological behavior of hard rock using triaxial rheological experiment. Int J Rock Mech Min Sci, 2017, 93: 66 doi: 10.1016/j.ijrmms.2017.01.004 [24] Zhao Y L, Zhang L Y, Wang W J, et al. Creep behavior of intact and cracked limestone under multi-level loading and unloading cycles. Rock Mech Rock Eng, 2017, 50(6): 1409 doi: 10.1007/s00603-017-1187-1 [25] Kilbas A A, Srivastava H M, Trujillo J J. Theory and Applications of Fractional Differential Equations. Amsterdam: Elsevier Press, 2006 [26] Qin Y P, Wang L, Sun W B, et al. Study on rheological theory model of rock damage. Chin J Rock Mech Eng, 2002, 21(Suppl 2): 2291秦躍平, 王林, 孫文標, 等. 巖石損傷流變理論模型研究. 巖石力學與工程學報, 2002, 21(增刊2): 2291 -
點擊查看大圖
計量
- 文章訪問數: 1236
- HTML全文瀏覽量: 400
- PDF下載量: 46
- 被引次數: 0
