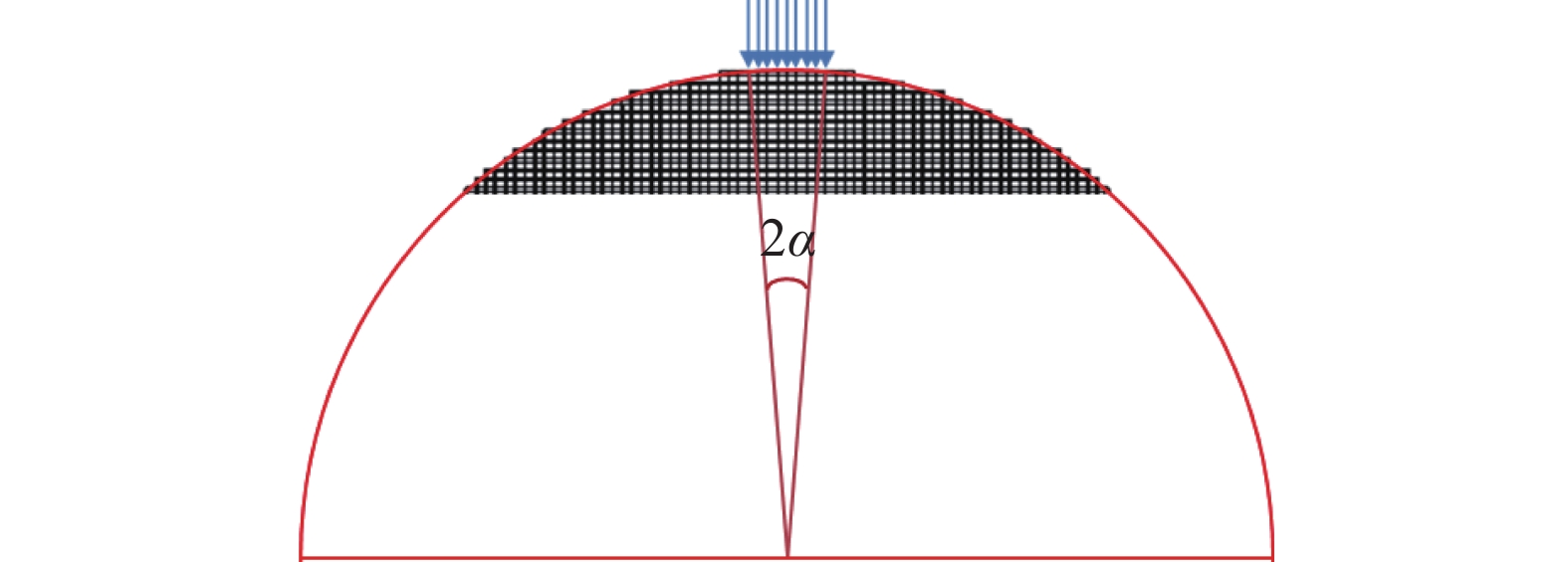
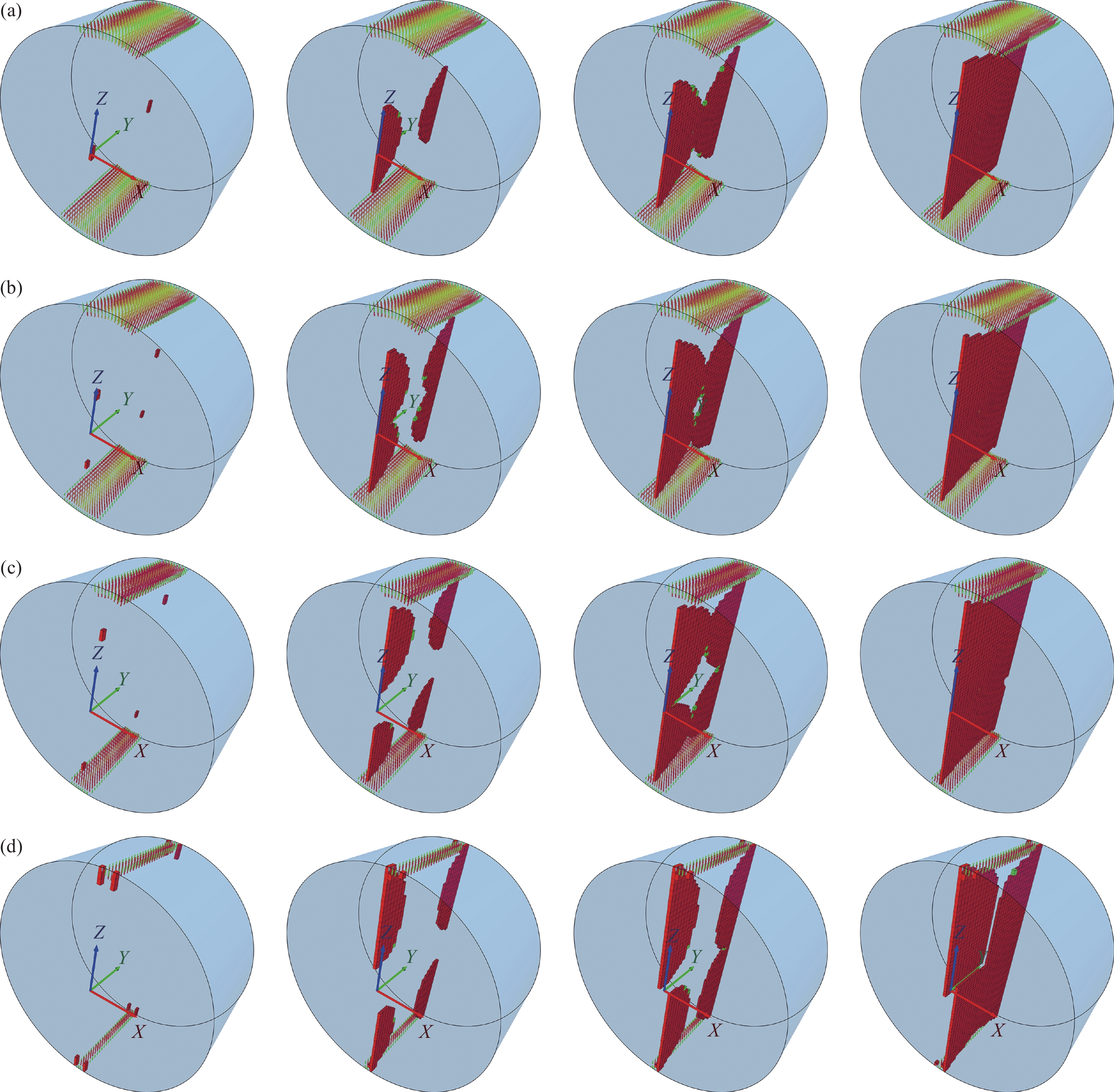
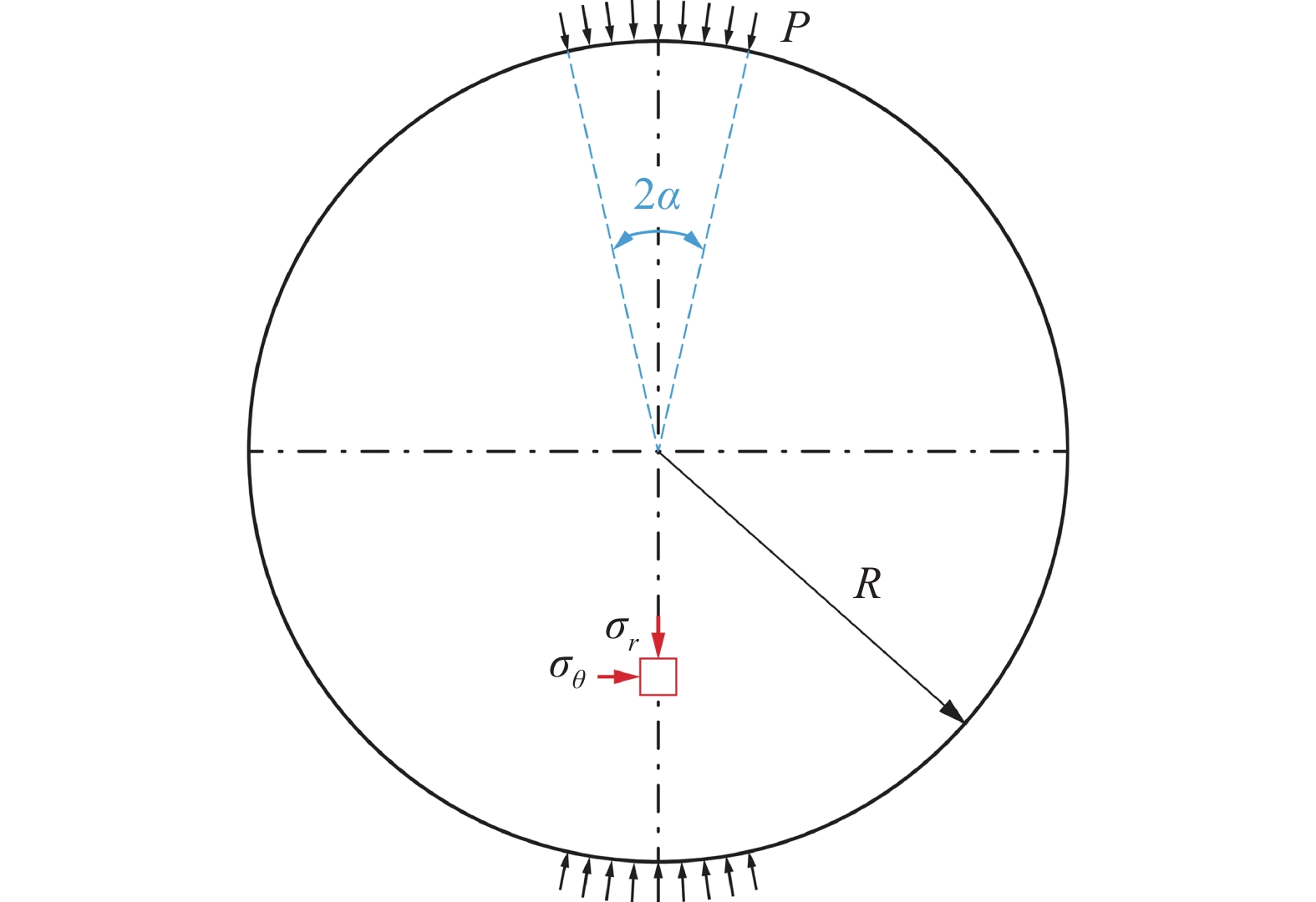
-
摘要: 為揭示巴西圓盤起裂模式的變化規律及其破裂演化過程，運用連續介質彈塑性分析開展巴西圓盤劈裂二維及三維數值模擬研究。通過開展二維模擬研究，探究壓拉比及加載角對試樣起裂破壞模式的影響；通過三維模擬研究，探究圓盤試樣三維破裂面的形成及擴展過程。二維數值模擬結果表明，接觸加載角及壓拉比越大，巴西圓盤試樣越容易發生中心起裂；端部起裂由剪切破壞引起，而劈裂裂紋進一步擴展則由張拉破壞驅動。三維數值模擬結果表明，初始起裂點位于三維圓盤端面，隨加載角增大其逐漸向端面圓心移動；當圓盤發生端面中心起裂時，三維破裂面以弧形邊界向試樣內部發散擴展。無論圓盤試樣發生中心起裂還是端部起裂，由于三維效應巴西劈裂試驗可能都會低估巖石的抗拉強度。Abstract: The Brazilian splitting test is widely used to determine the tensile strength of rocks and rock-like materials due to its easy sample preparation and an easier compressive test setup as an indirect testing method compared with performing a direct uniaxial tensile test. However, the accuracy of this method has also been criticized for a long time in the literature since its introduction. This paper carried out two-dimensional (2D)/three-dimensional (3D) numerical simulations of the Brazilian tensile test using a continuum elastoplastic analysis to reveal the variation of fracture modes of the Brazilian disk and its fracture evolution process. The effect of compression-tension ratios and contact loading angles on the fracture modes of the disk specimens was studied through 2D simulations. Through 3D simulations, the initiation and expansion processes of the 3D fracture under different loading angles were explored. The simulated results of failure modes, stress distributions, and calculated tensile strengths were analyzed. The 2D numerical results show that the larger the contact loading angle and the compression–tension ratio, the more likely the Brazilian disk specimens crack first at the disk center. The fracture initiation under the loading rims is caused by shear failure, but further propagation of the split fracture is driven by tension failure. The 3D numerical simulation results show that the crack initiation point is always located on the end face of the disk and gradually moves to the center from the loading ends as the loading angle increases. When the central tensile cracking appears, the 3D fracture expanded toward the inside of the specimen with an arc boundary. Regardless of whether the disk specimen starts to fracture initially at the disk center or the loading points, the Brazilian tensile test may underestimate the tensile strength of rocks due to the 3D effect.
-
Key words:
- Brazilian test /
- numerical simulation /
- compression–tension ratio /
- loading angle /
- 3D fracture
-
圖 1 巴西圓盤弧形均布載荷加載示意圖
Figure 1. A disk subjected to diametrically distributed loads in the Brazilian test
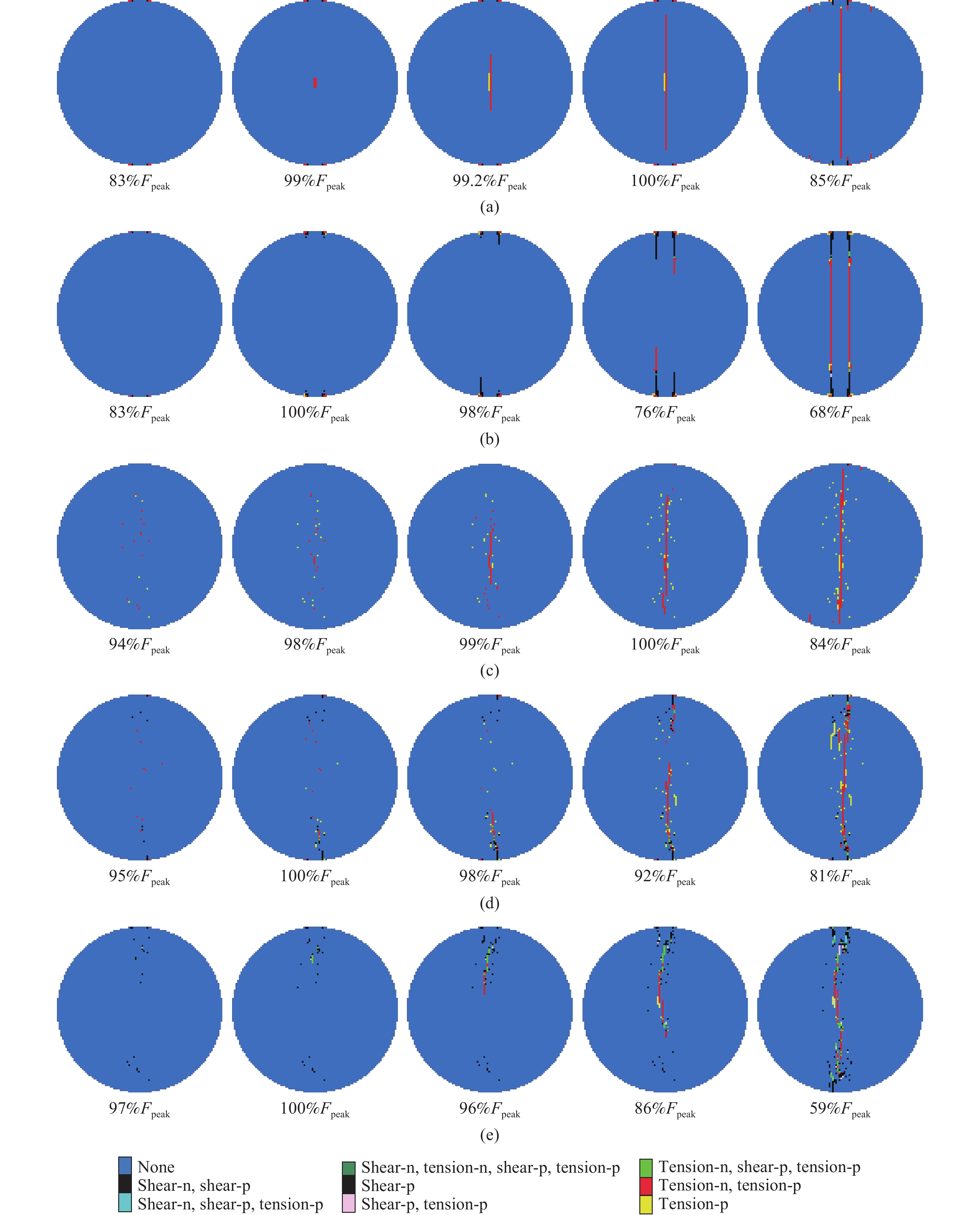
圖 3 不同壓拉比時巴西圓盤試樣的破壞過程。 （a）均勻試樣λ=20；（b） 均勻試樣λ=10；（c）非均勻試樣λ=20；（d）非均勻試樣λ=10；（e）非均勻試樣λ=8
Figure 3. Failure processes of the numerical disks with different compression–tension ratios (λ) under the loading angle of 9.18°: (a) homogeneous disk λ = 20; (b) homogeneous disk λ = 10; (c) heterogeneous disk λ = 20; (d) heterogeneous disk λ = 10; (e) heterogeneous disk λ = 8
圖 5 不同加載角時巴西圓盤試樣三維破裂面的起裂及擴展過程。 （a）2α=29.7°；（b）2α=25.7°；（c）2α=14.4°；（d）2α=4.4°
Figure 5. Fracture initiation and propagation processes of the 3D Brazilian disks with different contact loading angles: (a) 2α = 29.7°; (b) 2α = 25.7°; (c) 2α = 14.4°; (d) 2α = 4.4°
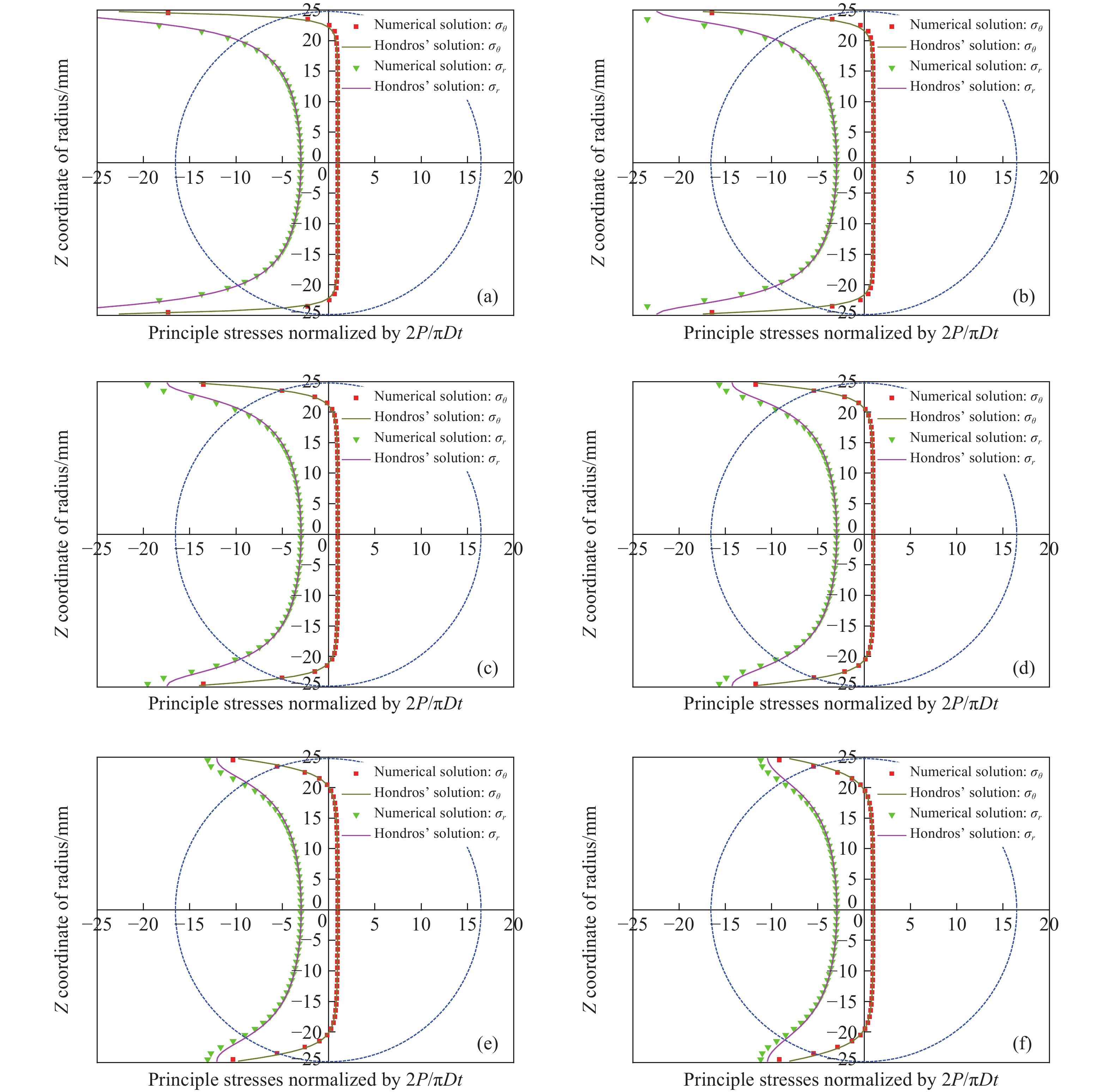
圖 6 不同加載角時二維巴西圓盤受壓直徑上應力分布的數值模擬結果與理論計算結果對比示意圖。 （a） 2α=4.58°；（b）2α=6.88°；（c）2α=9.18°；（d）2α=11.48°；（e）2α=13.78°；（f）2α=16.10°
Figure 6. Comparison of normalized stresses along the compressed diameter between the numerical results and Hondros’ solutions with different contact loading angles: (a) 2α = 4.58°; (b) 2α = 6.88°; (c) 2α = 9.18°; (d) 2α = 11.48°; (e) 2α = 13.78°; (f) 2α = 16.10°
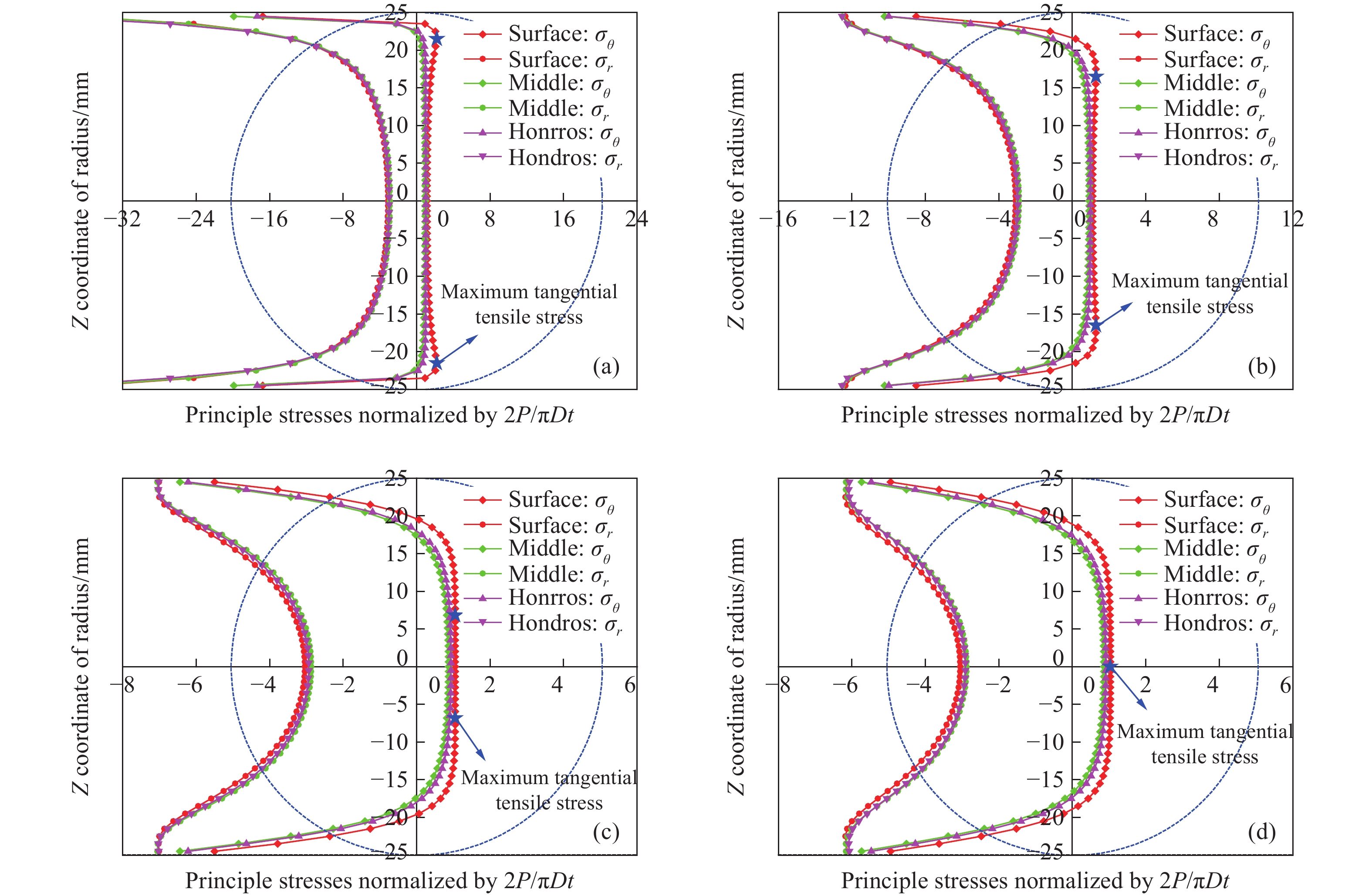
圖 7 不同加載角下三維巴西圓盤受壓直徑上應力分布的數值模擬結果與理論計算結果對比示意圖。（a）2α=4.4°；（b）2α=14.4°；（c）2α=25.7°；（d）2α=29.7°
Figure 7. Comparison of normalized stresses along the compressed diameter between the numerical results and Hondros’ solutions with different contact loading angles: (a) 2α = 4.4°; (b) 2α = 14.4°; (c) 2α = 25.7°; (d) 2α = 29.7°
圖 8 不同加載角下三維巴西圓盤試樣中心剖面及端面受壓直徑上切向應力分布示意圖。（a）中心剖面（Y=0.0125）切向應力；（b）端面（Y=0.025）切向應力
Figure 8. Normalized tangential stresses along the compressed diameter of the surface and middle section of 3D disks with different contact loading angles: (a) middle section (Y=0.0125); (b) surface (Y=0.025)
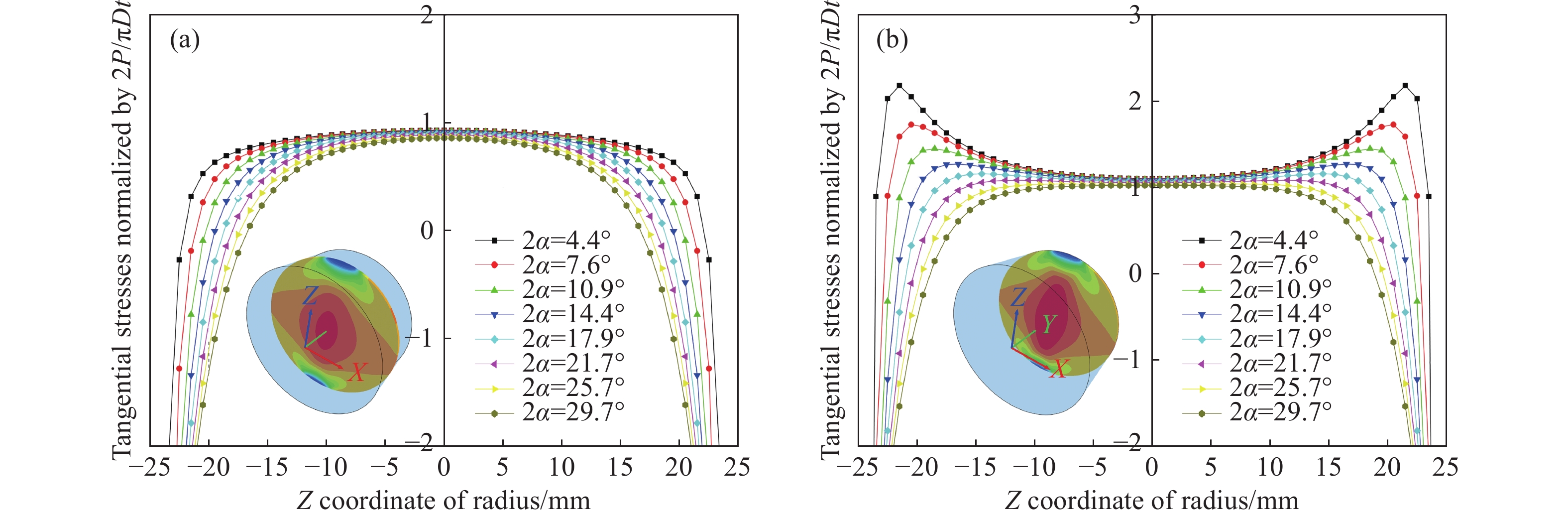
圖 9 不同加載角時三維巴西圓盤試樣軸向受壓平面上（X=0）切向應力分布云圖。（a）2α=29.7°；（b）2α=25.7°；（c）2α=14.4°；（d）2α=7.6°；（e）2α=4.4°
Figure 9. Contour plots of normalized tangential stresses (σxx) on the compressed middle section plane (X = 0) of the 3D disks with different contact loading angles: (a) 2α = 29.7°; (b) 2α = 25.7°; (c) 2α = 14.4°; (d) 2α = 7.6°; (e) 2α = 4.4°
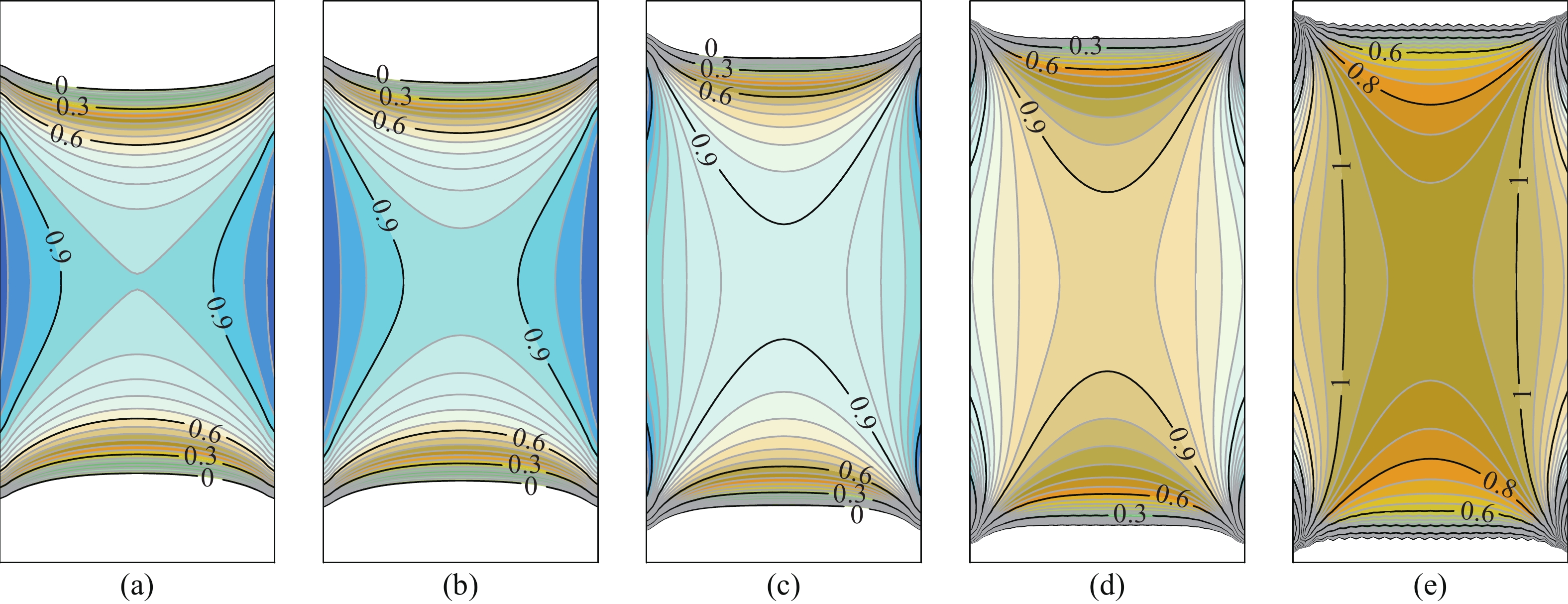
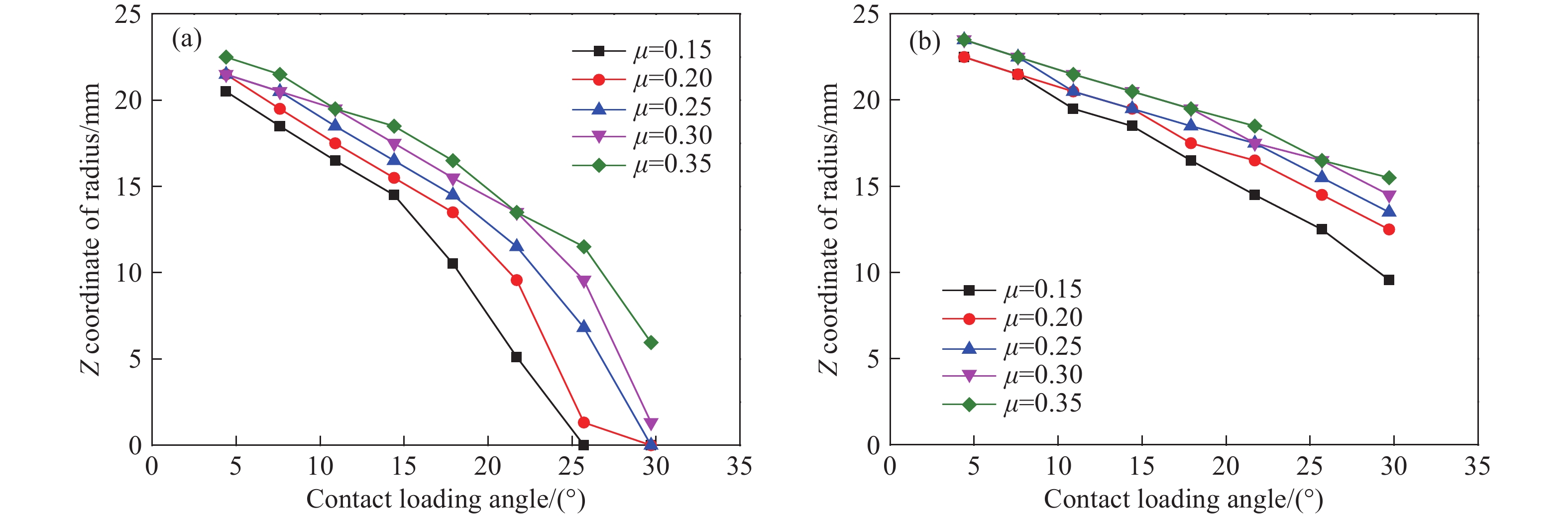
圖 10 不同泊松比時最大切向拉應力點及最大切向拉應變點位置隨接觸加載角的變化情況。（a）最大切向拉應力點；（b）最大切向拉應變點
Figure 10. Change in the position of the maximum tangential tensile stress point and strain point with the contact loading angles under different Poisson’s ratios: (a) the maximum tangential tensile stress point; (b) the maximum tangential tensile strain point
圖 11 最大Griffith等效拉應力位置隨加載角度的變化情況
Figure 11. Change in the position of the maximum Griffith equivalent tensile stresses with the contact loading angles
表 1 數值模型參數
Table 1. Material properties of the numerical model
Elastic modulus/
GPaPoisson’s ratio Compressive strength/
MPaTensile strength/
MPaCohesion/
MPa60 0.25 200 8 38.39 Friction angle/
(°)Residue cohesion/
MPaResidue tensile strength/
MPaPlastic shear strain limit Plastic tension strain limit 48 1.92 0.4 5 × 10?4 2 × 10?4 
下載: 導出CSV
表 2 不同壓拉比及加載角巴西試樣的破壞模式
Table 2. Failure modes of the numerical Brazilian disks with different compression?tension ratios (λ) and contact loading angles (2α)
λ Failure modes 2α = 16.10° 2α = 13.78° 2α = 11.48° 2α = 9.18° 2α = 6.88° 2α = 4.58° 20 
18 
16 
14 
12 
10 
下載: 導出CSV
表 3 不同加載角及壓拉比下二維巴西圓盤試樣抗拉強度計算結果
Table 3. Calculated tensile strength of 2D numerical Brazilian disks with different contact loading angles and compression–tension ratios
λ Real strength/MPa Calculated tensile strength/MPa 2α = 16.10° 2α = 13.78° 2α = 11.48° 2α = 9.18° 2α = 6.88° 2α = 4.58° 20 10.0 10.3 (2.6%) 10.2 (2.2%) 10.2 (1.7%) 10.1 (1.4%) 10.1 (1.2%) 8.7 (13.3%) 18 11.1 11.4 (2.5%) 11.3 (2.0%) 11.3 (1.6%) 11.3 (1.3%) 10.7 (3.3%) 8.6 (22.6%) 16 12.5 12.8 (2.5%) 12.7 (1.9%) 12.7 (1.5%) 12.1 (3.4%) 11.3 (9.7%) 8.7 (30.8%) 14 14.3 14.6 (2.2%) 14.5 (1.6%) 14.5 (1.2%) 11.9 (16.7%) 11.6 (19.0%) 8.7 (39.5%) 12 16.7 16.8 (1.0%) 16.3 (2.5%) 14.7 (12.1%) 11.7 (29.9%) 10.7 (35.6%) 8.6 (48.3%) 10 20.0 17.0 (14.8%) 16.6 (17.0%) 14.6 (26.8%) 12.9 (35.7%) 10.7 (46.7%) 8.6 (56.9%) Note: The data in parentheses are relative errors.
下載: 導出CSV
表 4 不同加載角下三維巴西圓盤試樣抗拉強度計算結果
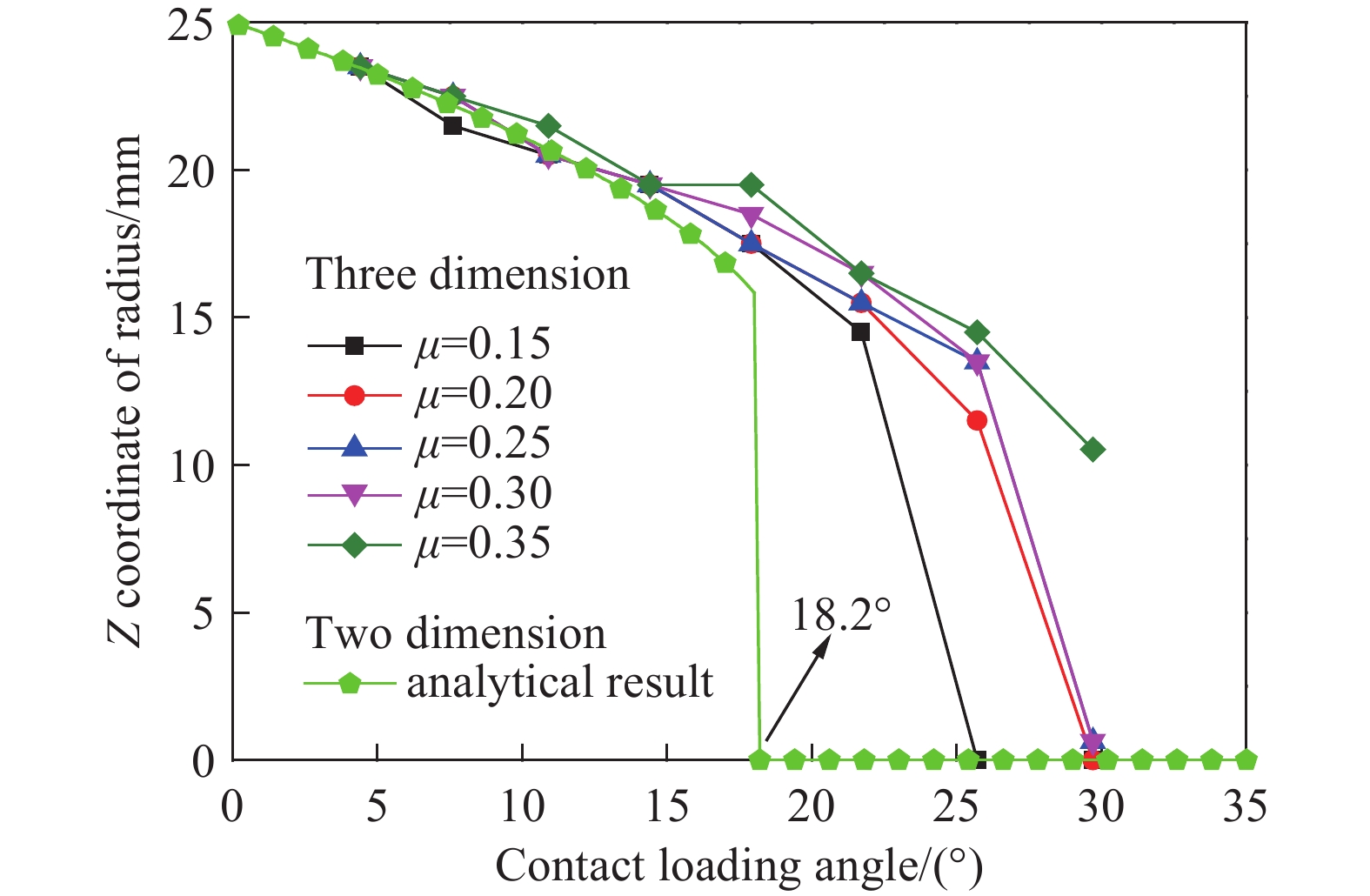
Table 4. Calculated tensile strength of the 3D numerical Brazilian disks with different loading angles
Loading angles/
(°)Peak loads/
NTensile strength/
MPaRelative error/
%Distance/
mmFailure modes 4.4 5427 2.76 65.5 25 Crack initiation at loading point 7.6 8329 4.22 47.3 20.5 Crack initiation off central point 10.9 10100 5.08 36.5 18.5 Crack initiation off central point 14.4 11784 5.88 26.5 17.5 Crack initiation off central point 17.9 13237 6.52 18.5 14.5 Crack initiation off central point 21.7 14132 6.86 14.3 12.5 Crack initiation off central point 25.7 14925 7.10 11.3 8.5 Crack initiation off central point 29.7 15441 7.17 10.4 0 Crack initiation at central point 33.7 15868 7.16 10.4 0 Crack initiation at central point
下載: 導出CSV
www.77susu.com<span id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> <span id="fpn9h"><noframes id="fpn9h"> <th id="fpn9h"></th> <strike id="fpn9h"><noframes id="fpn9h"><strike id="fpn9h"></strike> <th id="fpn9h"><noframes id="fpn9h"> <span id="fpn9h"><video id="fpn9h"></video></span> <ruby id="fpn9h"></ruby> <strike id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> -
參考文獻
[1] Healy D, Jones R R, Holdsworth R E. Three-dimensional brittle shear fracturing by tensile crack interaction. Nature, 2006, 439(7072): 64 doi: 10.1038/nature04346 [2] Reches Z, Lockner D A. Nucleation and growth of faults in brittle rocks. J Geophys Res Solid Earth, 1994, 99(B9): 18159 doi: 10.1029/94JB00115 [3] Hoek E, Martin C D. Fracture initiation and propagation in intact rock—a review. J Rock Mech Geotech Eng, 2014, 6(4): 287 doi: 10.1016/j.jrmge.2014.06.001 [4] International Society for Rock Mechanics. Suggested methods for determining tensile strength of rock materials. Int J Rock Mech Min Sci Geomech Abstr, 1978, 15(3): 99 doi: 10.1016/0148-9062(78)90003-7 [5] Fairhurst C. On the validity of the ‘Brazilian’ test for brittle material. Int J Rock Mech Min Sci Geomech Abstracts, 1964, 1(4): 535 doi: 10.1016/0148-9062(64)90060-9 [6] Yu Y. Questioning the validity of the Brazilian test for determining tensile strength of rocks. Chin J Rock Mech Eng, 2005, 24(7): 1150 doi: 10.3321/j.issn:1000-6915.2005.07.011喻勇. 質疑巖石巴西圓盤拉伸強度試驗. 巖石力學與工程學報, 2005, 24(7):1150 doi: 10.3321/j.issn:1000-6915.2005.07.011 [7] Li D Y, Wong L N Y. The Brazilian disc test for rock mechanics applications: review and new insights. Rock Mech Rock Eng, 2013, 46(2): 269 doi: 10.1007/s00603-012-0257-7 [8] Erarslan N, Williams D J. Experimental, numerical and analytical studies on tensile strength of rocks. Int J Rock Mech Min Sci, 2012, 49: 21 doi: 10.1016/j.ijrmms.2011.11.007 [9] Erarslan N, Liang Z Z, Williams D J. Experimental and numerical studies on determination of indirect tensile strength of rocks. Rock Mech Rock Eng, 2012, 45(5): 739 [10] Komurlu E, Kesimal A, Demir S. Experimental and numerical study on determination of indirect (splitting) tensile strength of rocks under various load apparatus. Can Geotech J, 2016, 53(2): 360 doi: 10.1139/cgj-2014-0356 [11] Komurlu E, Kesimal A. Evaluation of indirect tensile strength of rocks using different types of jaws. Rock Mech Rock Eng, 2015, 48(4): 1723 doi: 10.1007/s00603-014-0644-3 [12] Jaeger J C, Hoskins E R. Rock failure under the confined Brazilian test. J Geophys Res, 1966, 71(10): 2651 doi: 10.1029/JZ071i010p02651 [13] García V J, Márquez C M, Zú?iga-Suárez A R, et al. Brazilian test of concrete specimens subjected to different loading geometries: review and new insights. Int J Concr Struct Mater, 2017, 11(2): 343 doi: 10.1007/s40069-017-0194-7 [14] Gutiérrez-Moizant R, Ramírez-Berasategui M, Santos-Cuadros S, et al. Computational verification of the optimum boundary condition of the Brazilian tensile test. Rock Mech Rock Eng, 2018, 51(11): 3505 doi: 10.1007/s00603-018-1553-7 [15] Bahaaddini M, Serati M, Masoumi H, et al. Numerical assessment of rupture mechanisms in Brazilian test of brittle materials. Int J Solids Struct, 2019, 180-181: 1 doi: 10.1016/j.ijsolstr.2019.07.004 [16] Han Y F, Wang Z H, Tang Y S. Mechanical behavior of different rocks in the splitting test. J China Univ Min Technol, 2020, 49(5): 863韓宇峰, 王兆會, 唐岳松. 劈裂實驗中不同巖石力學行為特征. 中國礦業大學學報, 2020, 49(5):863 [17] Aliabadian Z, Zhao G F, Russell A R. Crack development in transversely isotropic sandstone discs subjected to Brazilian tests observed using digital image correlation. Int J Rock Mech Min Sci, 2019, 119: 211 doi: 10.1016/j.ijrmms.2019.04.004 [18] Deng H F, Li J L, Zhu M, et al. Research on effect of disc thickness-to-diameter ratio on splitting tensile strength of rock. Chin J Rock Mech Eng, 2012, 31(4): 792鄧華鋒, 李建林, 朱敏, 等. 圓盤厚徑比對巖石劈裂抗拉強度影響的試驗研究. 巖石力學與工程學報, 2012, 31(4):792 [19] Xu X L. Research on the Experiment and Meso-simulation of Tensile Characteristics and Its Fracture Mechanism of Brittle Rock [Dissertation]. Beijing: University of Science and Technology Beijing, 2017許學良. 脆性巖石抗拉特性及其破裂機制的試驗與細觀研究[學位論文]. 北京: 北京科技大學, 2017 [20] Hondros J R. The evaluation of poisson's ratio and the modulus of materials of a low tensile resistance by the Brazilian (indirect tension) test with particular reference to concrete. Aust J Appl Sci, 1959, 10: 243 [21] Li D Y. Study on the Spalling Failure of Hard Rock and the Mechanism of Strainburst under High in-situ Stresses [Dissertation]. Changsha: Central South University, 2010李地元. 高應力硬巖脆性板裂破壞和應變型巖爆機理研究[學位論文]. 長沙: 中南大學, 2010 [22] Chen S, Yue Z Q, Tan G H. Digital image based numerical modeling method for heterogeneous geomaterials. Chin J Geotech Eng, 2005, 27(8): 956 doi: 10.3321/j.issn:1000-4548.2005.08.020陳沙, 岳中琦, 譚國煥. 基于數字圖像的非均質巖土工程材料的數值分析方法. 巖土工程學報, 2005, 27(8):956 doi: 10.3321/j.issn:1000-4548.2005.08.020 [23] Liu J, Zhao G Y, Liang W Z, et al. Numerical simulation of uniaxial compressive strength and failure characteristics in nonuniform rock materials. Rock Soil Mech, 2018, 39(Suppl 1): 505劉建, 趙國彥, 梁偉章, 等. 非均勻巖石介質單軸壓縮強度及變形破裂規律的數值模擬. 巖土力學, 2018, 39(增刊1): 505 [24] Liang Z Z, Tang C A, Zhang Y B, et al. On probability model of physico-mechanical parameters of quasi-brittle materials and associated mechanical failure behaviors. Chin J Rock Mech Eng, 2008, 27(4): 718 doi: 10.3321/j.issn:1000-6915.2008.04.010梁正召, 唐春安, 張永彬, 等. 準脆性材料的物理力學參數隨機概率模型及破壞力學行為特征. 巖石力學與工程學報, 2008, 27(4):718 doi: 10.3321/j.issn:1000-6915.2008.04.010 [25] Jiang Q, Cui J, Feng X T, et al. Stochastic statistics and probability distribution estimation of mechanical parameters of basalt. Rock Soil Mech, 2017, 38(3): 784江權, 崔潔, 馮夏庭, 等. 玄武巖力學參數的隨機性統計與概率分布估計. 巖土力學, 2017, 38(3):784 [26] Yang Z P, He B, Xie L Z, et al. Strength and failure modes of shale based on Brazilian test. Rock Soil Mech, 2015, 36(12): 3447楊志鵬, 何柏, 謝凌志, 等. 基于巴西劈裂試驗的頁巖強度與破壞模式研究. 巖土力學, 2015, 36(12):3447 [27] Stacey T R. A simple extension strain criterion for fracture of brittle rock. Int J Rock Mech Min Sci Geomech Abstracts, 1981, 18(6): 469 doi: 10.1016/0148-9062(81)90511-8 -
點擊查看大圖
計量
- 文章訪問數: 1869
- HTML全文瀏覽量: 753
- PDF下載量: 139
- 被引次數: 0
