Experimental study on concrete beams without web reinforcement based on fractal theory
-
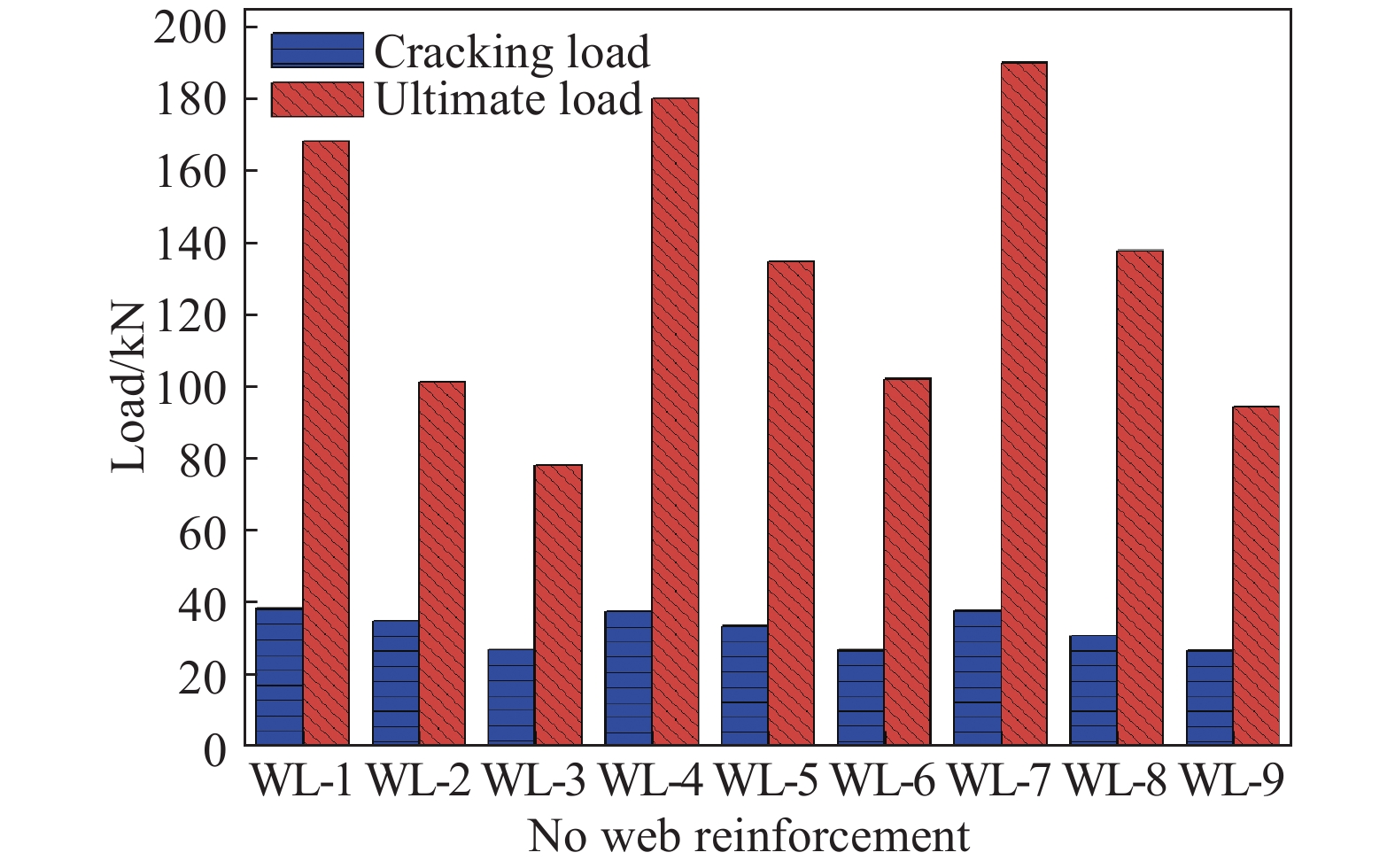
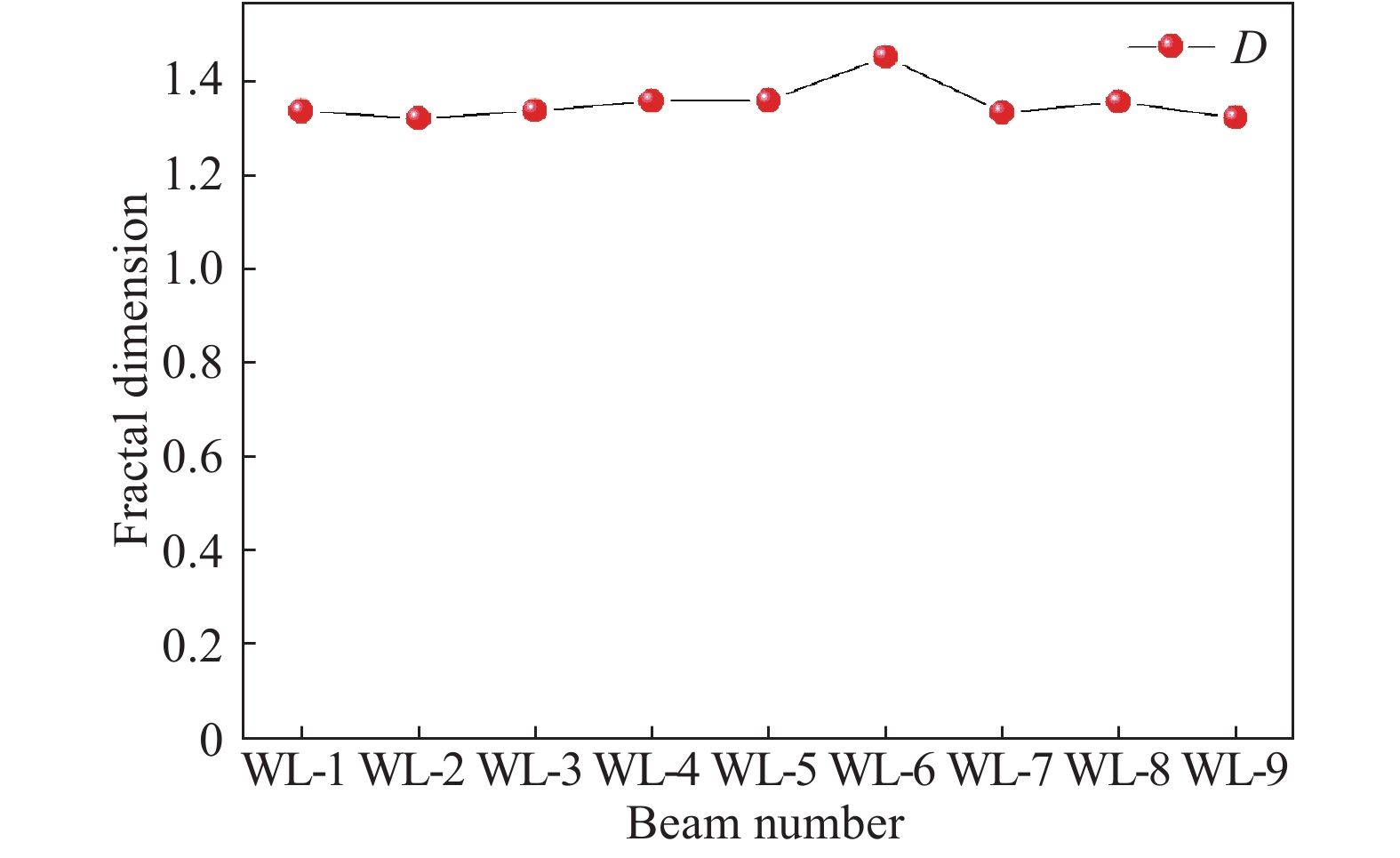
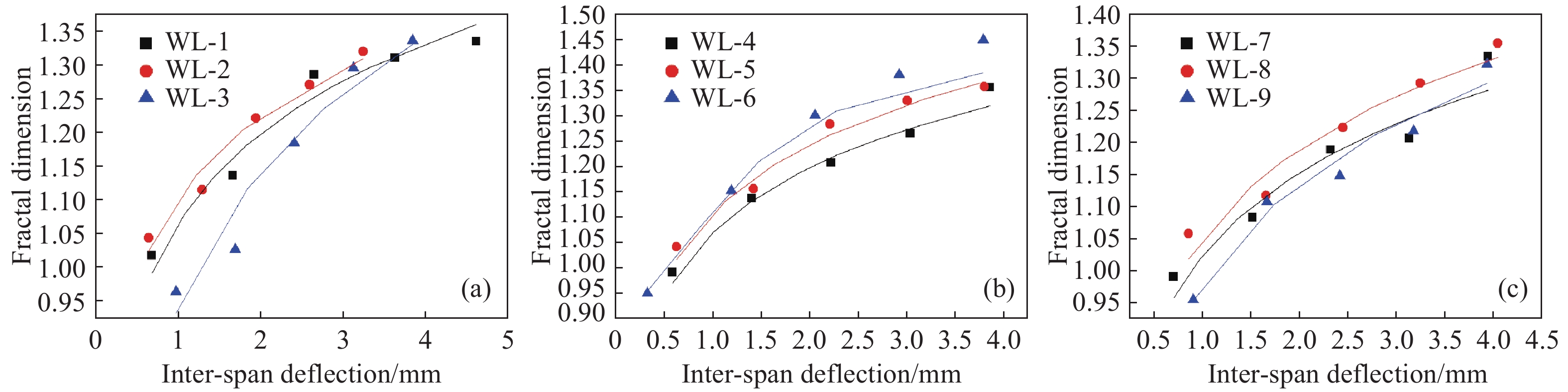
摘要: 基于裂縫的發展及分布形態，探究無腹筋混凝土梁在不同剪跨比和縱筋配筋率作用下的剪切性能，采用剪跨比分別為1.5、2、2.5和縱筋配筋率分別為1.28%、1.62%、1.99%的9組無腹筋混凝土梁進行四點加載受剪試驗，通過應用分形幾何理論對試驗梁表面的裂縫進行分析，使用盒計數法計算得到分級荷載及極限荷載作用下梁表面裂縫的分形維數，探討了梁表面分形維數與極限荷載、分級荷載及跨中撓度之間的關系。結果表明：剪跨比與極限荷載及開裂荷載成反比，而縱筋配筋率與極限荷載成正比，但其對于開裂荷載的影響較小。無腹筋混凝土梁不論在分級加載作用下還是極限荷載作用下都具備明顯的分形特征，在分級荷載作用下的分形維數在0.964～1.449，在極限荷載作用下的分形維數在1.33附近。分級荷載、跨中撓度與分形維數之間呈現較好的對數關系，分級荷載與分形維數的變化曲線受剪跨比及梁縱筋配筋率的影響具有一定的規律性，而跨中撓度受剪跨比的影響較小，在縱筋配筋率作用下，其曲線的曲率呈現出先增大后減小的趨勢，但極限荷載與分形維數之間的關系具有一定的差異性，極限荷載會隨著剪跨比的增大呈現出先增大后減小的趨勢，隨著縱筋配筋率的增大呈現出的差異性較大。Abstract: Based on the development and distribution of cracks, we explored the shear performance of concrete beams without web reinforcement under different shear span ratios and longitudinal reinforcement ratios. Nine groups of concrete beams without web reinforcement with shear-span ratios of 1.5, 2, 2.5 and longitudinal reinforcement ratios of 1.28%, 1.62%, and 1.99% were used for four-point loading shear tests. The cracks on the surface of the test beam were analyzed by applying fractal geometry theory, and the box counting method was used to calculate the fractal dimension of the cracks on the surface of the beam under the effect of the graded load and the ultimate load. The relationship among the fractal dimension of the beam surface, the ultimate load, the graded load and the span was discussed. The results show that the shear-span ratio is inversely proportional to the ultimate load and cracking load, while the longitudinal reinforcement ratio is directly proportional to the ultimate load and exhibit a small influence on the cracking load. Concrete beams without web reinforcement have obvious fractal characteristics under the effect of graded loading or ultimate load. The fractal dimension under the effect of graded load is 0.964–1.449, and the fractal dimension under the effect of ultimate load is around 1.33. The graded load, mid-span deflection and fractal dimension show a good logarithmic relationship. The change curve of graded load and fractal dimension is affected by the shear-span ratio and the beam longitudinal reinforcement ratio. The intermediate deflection is less affected by the shear-span ratio. Under the effect of the longitudinal reinforcement ratio, the curvature of the curve shows a trend of first increasing and then decreasing, but the relationship between the ultimate load and the fractal dimension has certain differences. The ultimate load first increases and then decreases with the increase of the shear span ratio, and the difference is greater with the increase of the longitudinal reinforcement ratio.
-
圖 1 無腹筋梁尺寸及配筋圖（單位: mm）
Figure 1. Dimensions and reinforcement drawing of girder without rib (Unit: mm)
圖 2 加載裝置布置圖。（a）λ = 1.5；（b）λ = 2；（c）λ = 2.5；（d）現場布置圖
Figure 2. Load device layout: (a) λ = 1.5; (b) λ = 2; (c) λ = 2.5; (d) site layout
圖 3 試驗梁裂縫分布圖。（a）WL-1；（b）WL-2；（c）WL-3；（d）WL-4；（e）WL-5；（f）WL-6；（g）WL-7；（h）WL-8；（i）WL-9
Figure 3. Crack distribution of test beam: (a) WL-1; (b) WL-2; (c) WL-3; (d) WL-4; (e) WL-5; (f) WL-6; (g) WL-7; (h) WL-8; (i) WL-9
圖 4 相同剪跨比、不同縱筋配筋率作用下的荷載與撓度間關系。（a） λ = 1.5；（b）λ = 2；（c）λ = 2.5
Figure 4. Relationship between load and deflection under the same shear-span ratio and different longitudinal reinforcement ratios: (a) λ = 1.5; (b) λ = 2; (c) λ = 2.5
圖 5 相同縱筋配筋率、不同剪跨比作用下荷載與撓度間的關系。（a）ρ = 1.28%；（b）ρ = 1.62%；（c）ρ = 1.99%
Figure 5. Relationship between load and deflection under the same longitudinal reinforcement ratio and different shear span ratios: (a) ρ = 1.28%; (b) ρ = 1.62%; (c) ρ = 1.99%
圖 7 不同等級荷載下梁表面的lnN(L)–ln(1/L)圖。（a）WL-1；（b）WL-2；（c）WL-3；（d）WL-4；（e）WL-5；（f）WL-6；（g）WL-7；（h）WL-8；（i）WL-9
Figure 7. lnN(L)–ln(1/L) diagram of beam surface under different grades of load: (a) WL-1; (b) WL-2; (c) WL-3; (d) WL-4; (e) WL-5; (f) WL-6; (g) WL-7; (h) WL-8; (i) WL-9
圖 8 極限荷載下梁表面的lnN(L)–ln(1/L)圖
Figure 8. lnN(L)–ln(1/L) diagram of the beam surface under ultimate load
圖 10 相同剪跨比、不同縱筋配筋率作用下的極限荷載與分形維數間的關系。（a）λ = 1.5；（b）λ = 2；（c）λ = 2.5
Figure 10. Relationship between ultimate load and fractal dimension under the same shear span ratio and different longitudinal reinforcement ratios: (a) λ = 1.5, (b) λ = 2, (c) λ = 2.5
圖 11 相同縱筋配筋率、不同剪跨比作用下的極限荷載與分形維數間的關系。（a）ρ = 1.28%；（b）ρ = 1.62%；（c）ρ = 1.99%
Figure 11. Relationship between ultimate load and fractal dimension under the same longitudinal reinforcement ratio and different shear span ratios: (a) ρ = 1.28%; (b) ρ = 1.62%; (c) ρ = 1.99%
圖 12 相同剪跨比、不同縱筋配筋率作用下的分級荷載與分形維數間關系。（a）λ = 1.5；（b）λ = 2；（c）λ = 2.5
Figure 12. Relationship between the graded load and the fractal dimension under the same shear span ratio and different longitudinal reinforcement ratios: (a) λ = 1.5; (b) λ = 2; (c) λ = 2.5
圖 13 相同縱筋配筋率、不同剪跨比作用下的分級荷載與分形維數間關系。（a）ρ = 1.28%；（b）ρ = 1.62%；（c）ρ = 1.99%
Figure 13. Relationship between the graded load and the fractal dimension under the same longitudinal reinforcement ratio and different shear span ratios: (a) ρ = 1.28%; (b) ρ = 1.62%; (c) ρ = 1.99%
圖 14 相同剪跨比、不同縱筋配筋率作用下的跨中撓度與分形維數間的關系。（a）λ = 1.5；（b）λ = 2；（c）λ = 2.5
Figure 14. Relationship between mid-span deflection and fractal dimension under the same shear-span ratio and different longitudinal reinforcement ratios: (a) λ = 1.5; (b) λ = 2; (c) λ = 2.5
圖 15 相同縱筋配筋率、不同剪跨比作用下的跨中撓度與分形維數間關系。（a）ρ = 1.28%；（b）ρ = 1.62%；（c）ρ = 1.99%
Figure 15. Relationship between mid-span deflection and fractal dimension under the same longitudinal reinforcement ratio and different shear-span ratios: (a) ρ = 1.28%; (b) ρ = 1.62%; (c) ρ = 1.99%
表 1 水泥的化學成分(質量分數)
Table 1. Chemical composition of cement
% SiO2 Al2O3 Fe2O3 CaO MgO SO3 K2O Na2O Li2O 21.22 5.05 3.26 60.24 0.97 2.67 0.50 0.73 — 
下載: 導出CSV
表 2 粗骨料的實驗性能
Table 2. Properties of coarse aggregate
Micron content/% Water absorption rate/% Needle-like content/% Ruggedness/
%Apparent density/(kg·m–3) 0.3 0.5 5 1 2640
下載: 導出CSV
表 3 試件參數信息
Table 3. Parameter information of test pieces
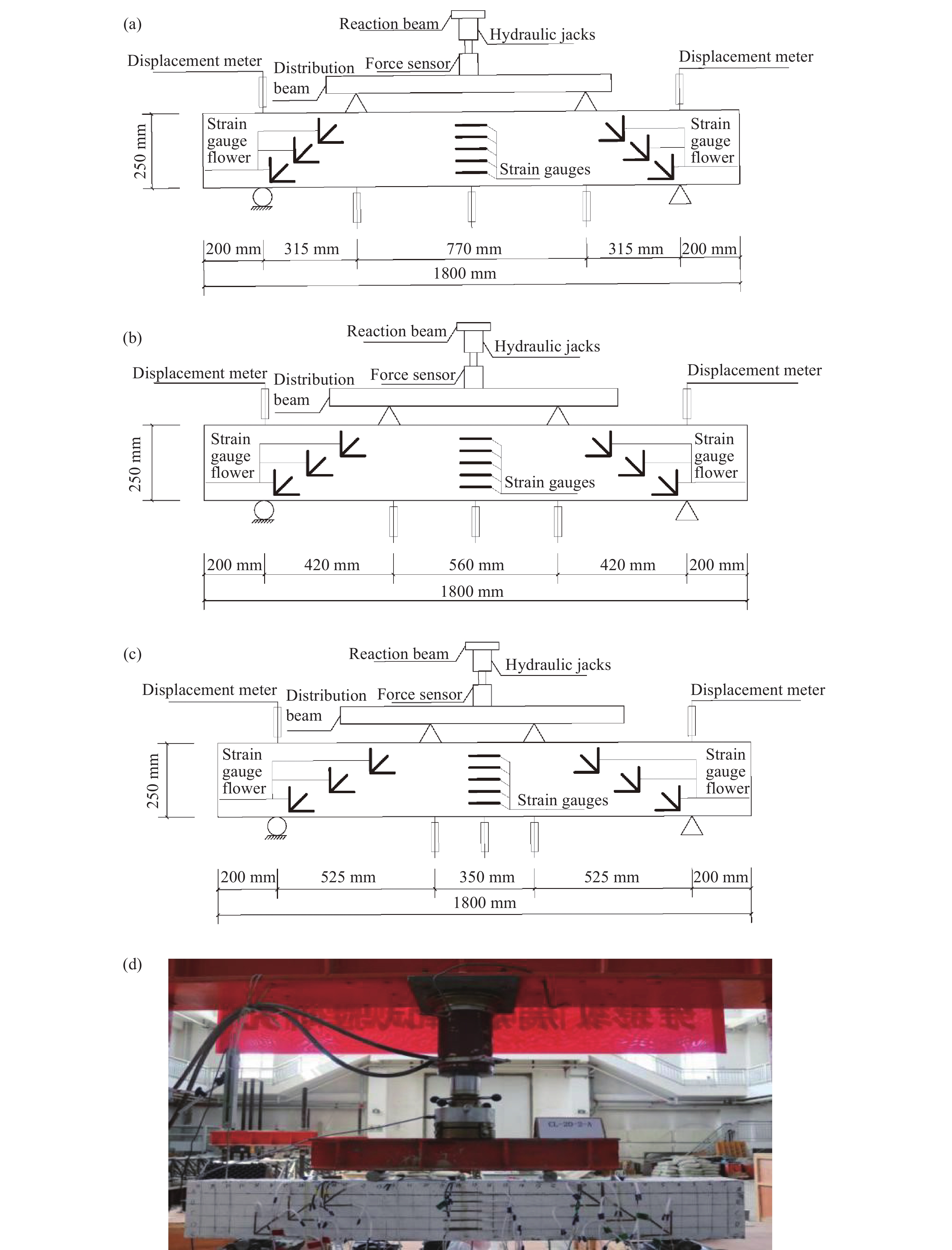
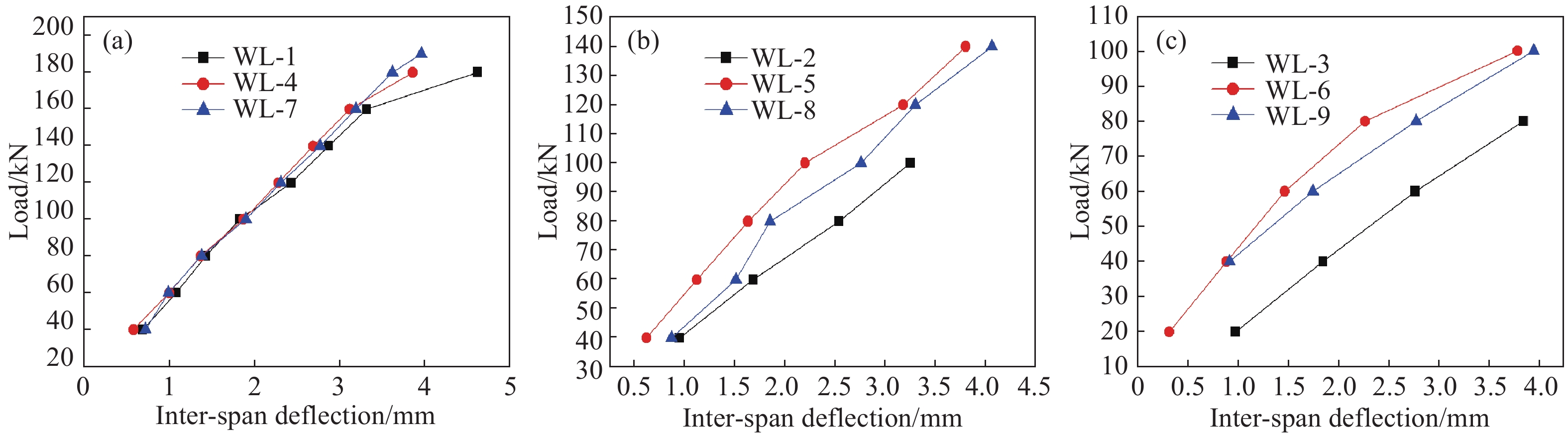
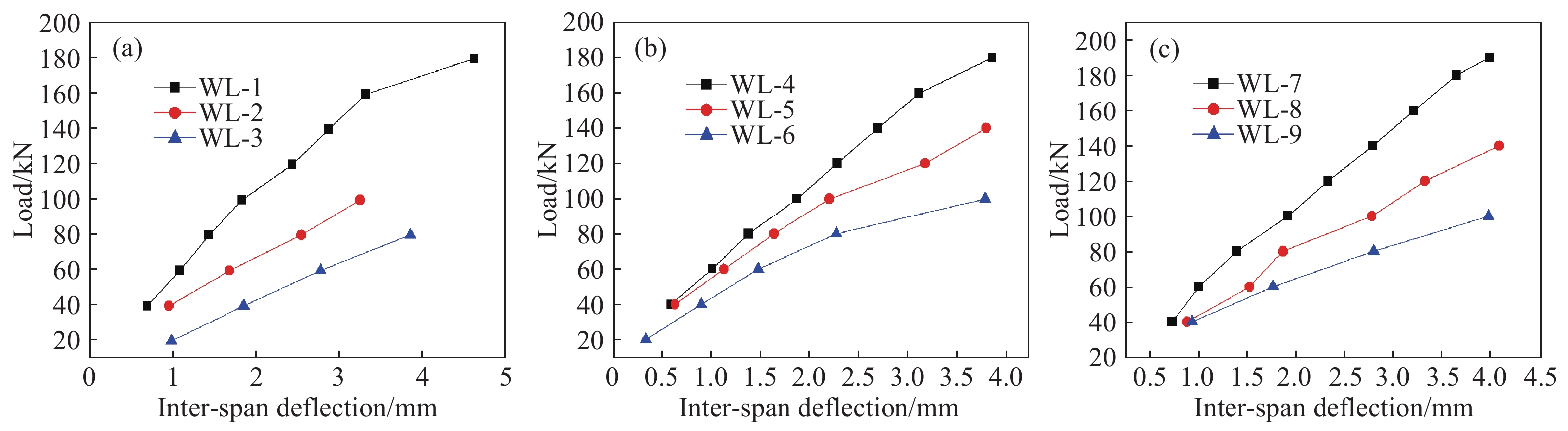
Numbering Size/mm Compressive strength/MPa Reinforcement diameter/mm Longitudinal strength Shear span ratio Reinforcement ratio/% WL-1 1800×150×250 41.031 16 HRB400 1.5 1.28 WL-2 1800×150×250 44.103 16 HRB400 2 1.28 WL-3 1800×150×250 42.772 16 HRB400 2.5 1.28 WL-4 1800×150×250 38.467 18 HRB400 1.5 1.62 WL-5 1800×150×250 37.003 18 HRB400 2 1.62 WL-6 1800×150×250 36.832 18 HRB400 2.5 1.62 WL-7 1800×150×250 38.607 20 HRB400 1.5 1.99 WL-8 1800×150×250 38.471 20 HRB400 2 1.99 WL-9 1800×150×250 46.219 20 HRB400 2.5 1.99
下載: 導出CSV
表 4 不同荷載作用下梁表面分形維數
Table 4. Fractal dimension of beam surface under different loads
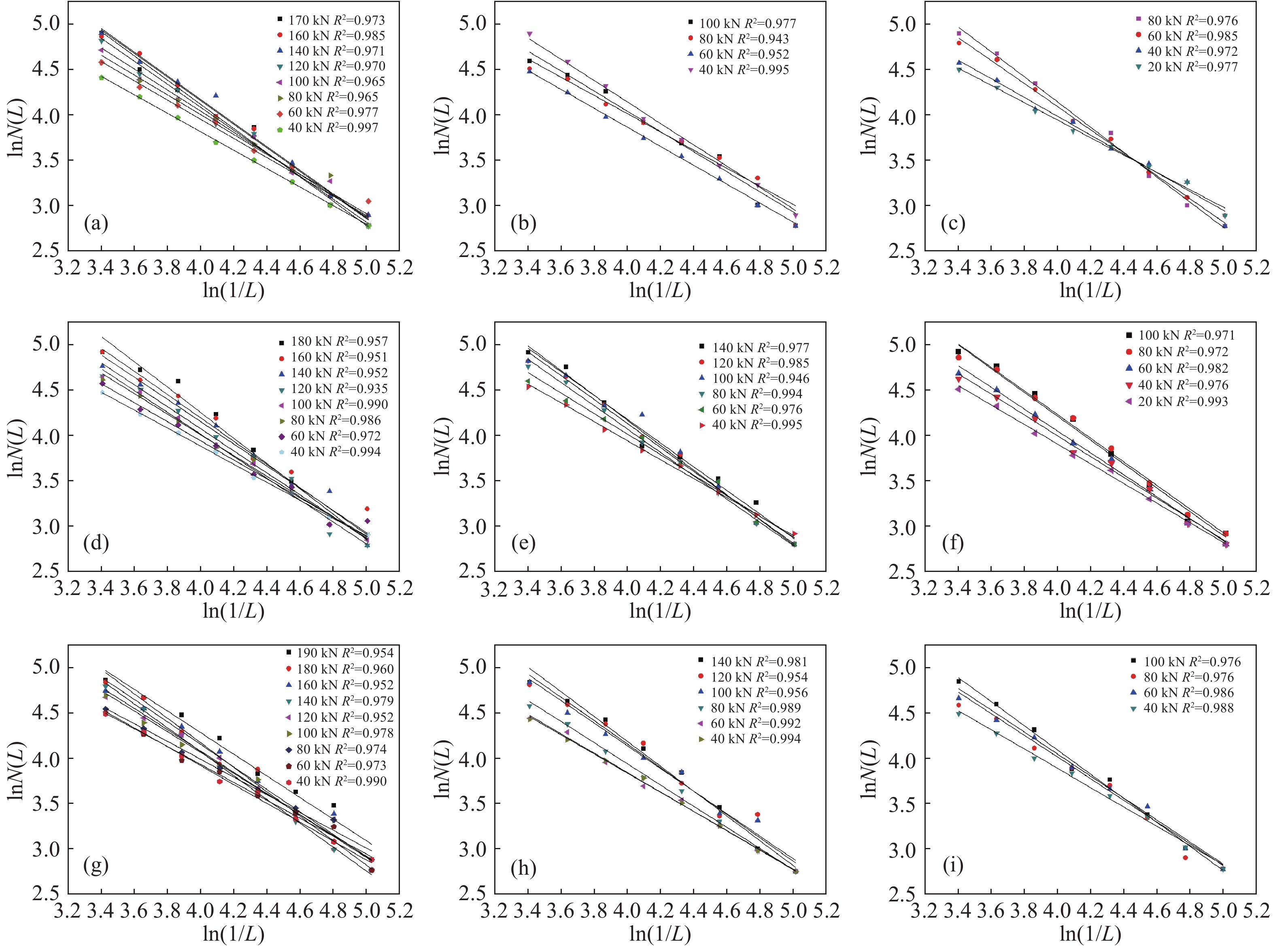
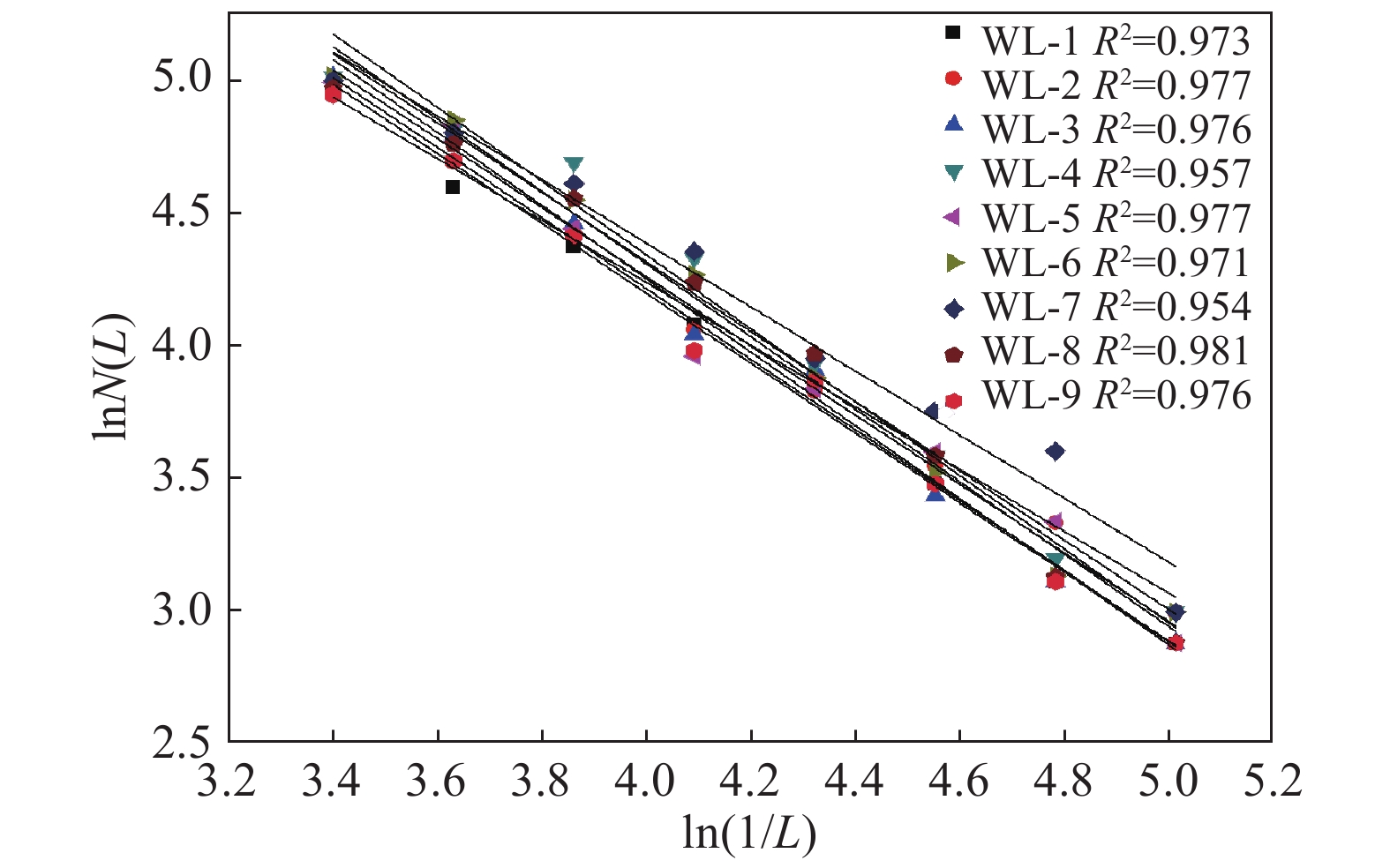
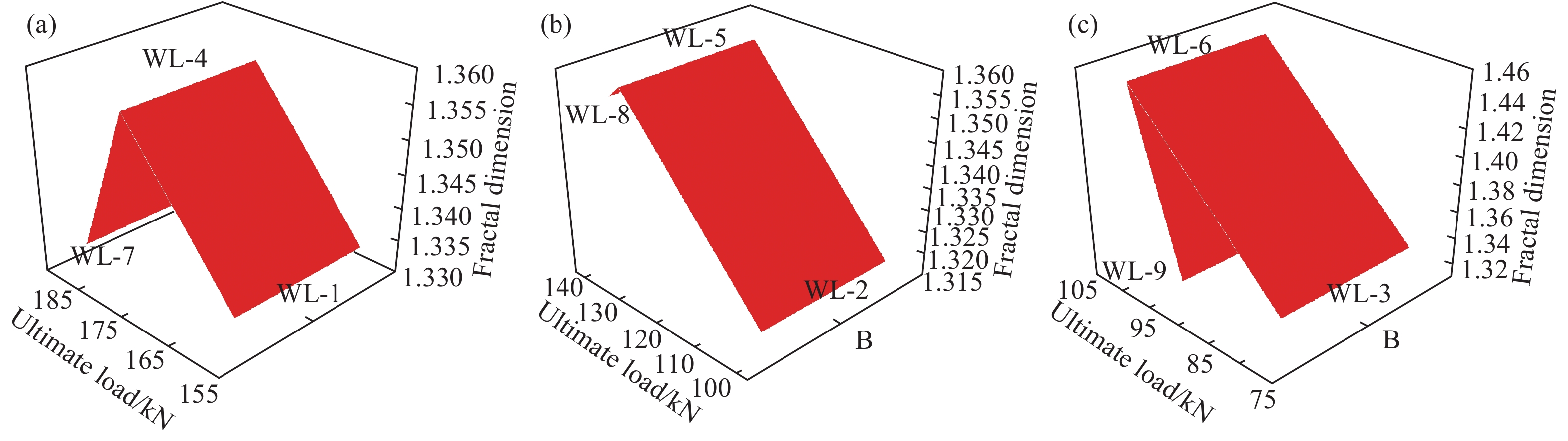
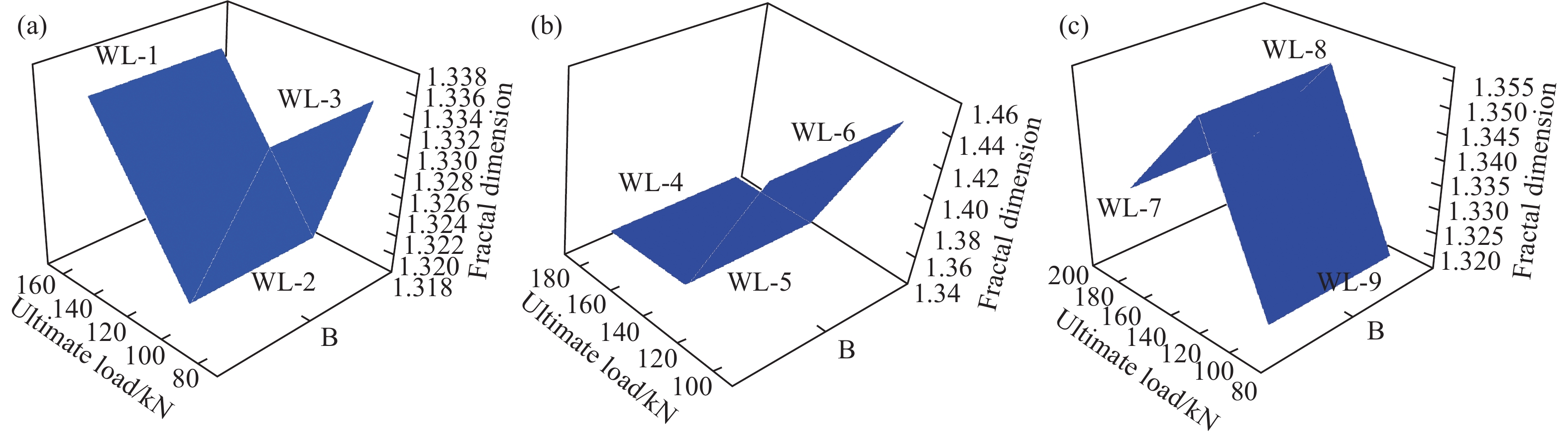
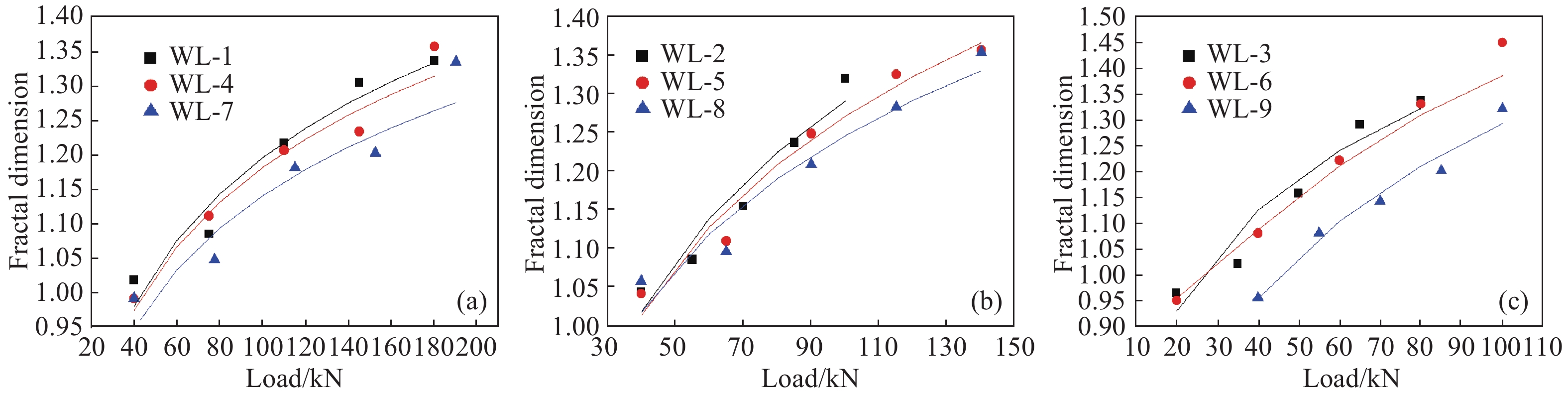
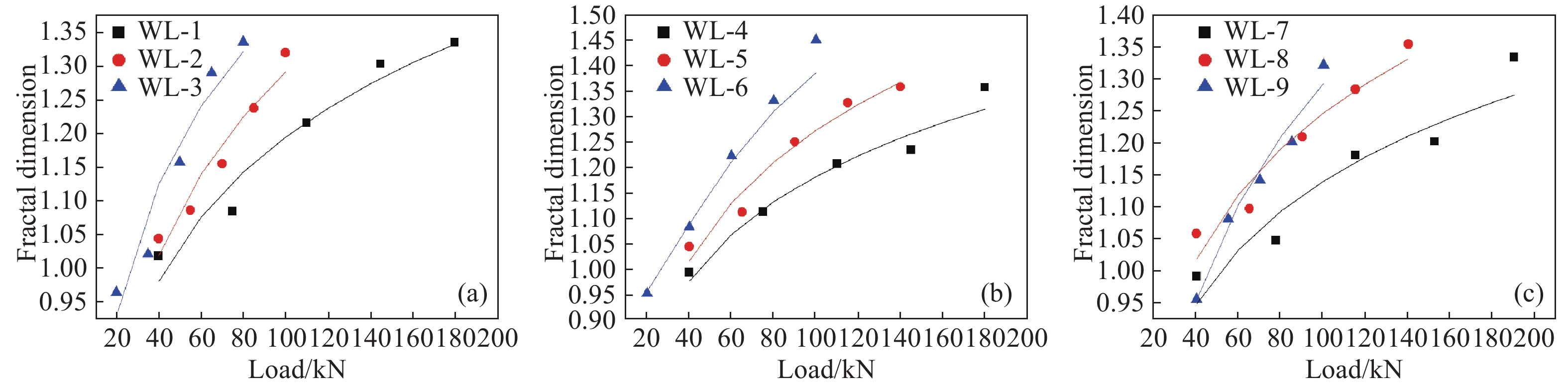
Load/kN Fractal dimension WL-1 WL-2 WL-3 WL-4 WL-5 WL-6 WL-7 WL-8 WL-9 20 — — 0.964 — — 0.951 — — — 40 1.018 1.044 1.040 0.991 1.042 1.082 0.991 1.058 0.955 60 1.059 1.1 1.275 1.044 1.075 1.221 0.999 1.072 1.122 80 1.093 1.21 1.336 1.133 1.215 1.330 1.054 1.170 1.161 100 1.164 1.32 — 1.203 1.283 1.449 1.157 1.248 1.321 120 1.267 — — 1.208 1.340 — 1.188 1.295 — 140 1.304 — — 1.218 1.357 — 1.193 1.354 — 160 1.302 — — 1.276 — — 1.207 — — 180 1.335 — — 1.356 — — 1.255 — — 190 — — — — — — 1.333 — —
下載: 導出CSV
表 5 分級荷載與分形維數關系的k、m值
Table 5. k, m values of the relationship between the graded load and the fractal dimension
Parameters WL-1 WL-2 WL-3 WL-4 WL-5 WL-6 WL-7 WL-8 WL-9 k 0.156 0.149 0.113 0.150 0.141 0.082 0.140 0.120 0.148 m 8.984 –6.25 6.25 8.827 –1.481 27.037 8.693 4.824 –20.653 R2 0.926 0.896 0.892 0.943 0.942 0.890 0.898 0.917 0.921
下載: 導出CSV
表 6 跨中撓度與分形維數關系的n、v值
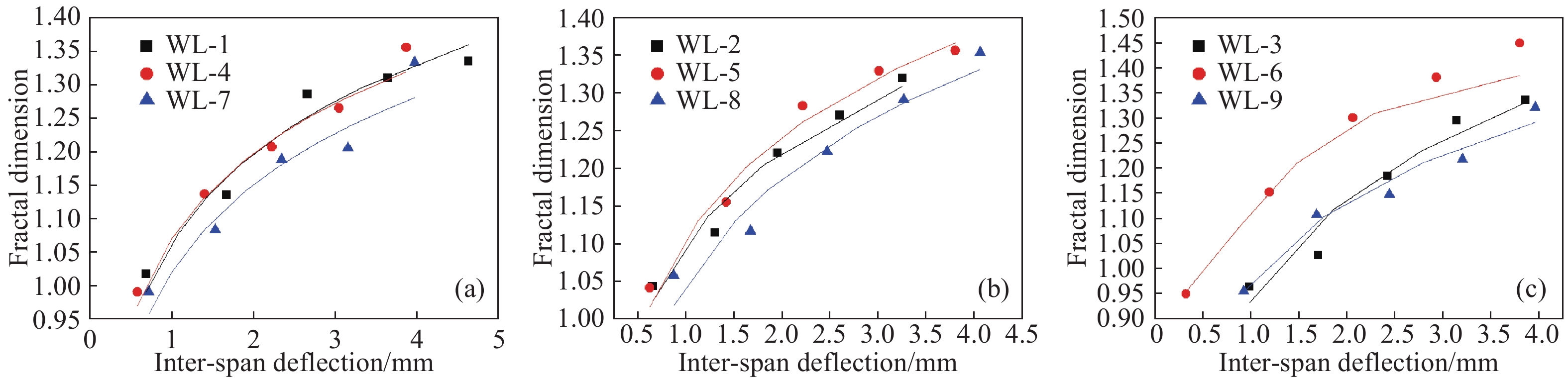
Table 6. n, v values of the relationship between the mid-span deflection and the fractal dimension
Parameters WL-1 WL-2 WL-3 WL-4 WL-5 WL-6 WL-7 WL-8 WL-9 n 0.129 0.108 0.116 0.123 0.097 0.056 0.126 0.102 0.093 v 83.047 82.727 73.281 66.049 68.457 75 51.307 52.613 48.898 R2 0.937 0.939 0.966 0.950 0.937 0.922 0.928 0.904 0.966
下載: 導出CSV
www.77susu.com<span id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> <span id="fpn9h"><noframes id="fpn9h"> <th id="fpn9h"></th> <strike id="fpn9h"><noframes id="fpn9h"><strike id="fpn9h"></strike> <th id="fpn9h"><noframes id="fpn9h"> <span id="fpn9h"><video id="fpn9h"></video></span> <ruby id="fpn9h"></ruby> <strike id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> -
參考文獻
[1] Du X L, Jie P L, Jin L. Dynamic flexural-tensile failure mode analysis of concrete beam with initial defect. Eng Mech, 2015, 32(2): 74杜修力, 揭鵬力, 金瀏. 考慮初始缺陷影響的混凝土梁動態彎拉破壞模式分析. 工程力學, 2015, 32(2):74 [2] Sun Y B, Yu G M, Zhang Y, et al. Fractal study on crack growth path of reinforced concrete beams fracture. Eng Constr, 2016, 48(7): 6孫葉冰, 于廣明, 張洋, 等. 鋼筋混凝土梁斷裂裂紋擴展路徑的分形研究. 工程建設, 2016, 48(7):6 [3] Tang C A, Zhu W C. A Numerical Experiment of Concrete Damage and Fracture. Beijing: Science Press, 2003唐春安, 朱萬成. 混凝土損傷與斷裂: 數值試驗. 北京: 科學出版社, 2003 [4] Mandelbort B B, Wheeler J A. The fractal geometry of nature. Am J Phys, 1983, 51(3): 286 doi: 10.1119/1.13295 [5] Ma X, Xie X P, Ye X W, et al. Fractal characteristics of pore structure of calcium-based geopolymer based on nitrogen adsorption. Mater Rev, 2019, 33(12): 1989 doi: 10.11896/cldb.18030014馬驍, 謝雪鵬, 葉雄偉, 等. 基于氮氣吸附法的鈣基地聚合物孔隙結構分形特征. 材料導報, 2019, 33(12):1989 doi: 10.11896/cldb.18030014 [6] Li G Q, Deng X J. Fractal effect of graded aggregate. Concrete, 1995(1): 3李國強, 鄧學鈞. 級配骨料的分形效應. 混凝土, 1995(1):3 [7] Zhou J H, Kang T B, Wang F C. Pore structure and carbonation fractal characteristics of waste fiber recycled concrete. Bull Chin Ceram Soc, 2017, 36(5): 1686周靜海, 康天蓓, 王鳳池. 廢棄纖維再生混凝土孔結構及碳化性能分形特征研究. 硅酸鹽通報, 2017, 36(5):1686 [8] Tian W, Dang F N, Chen H Q. Fractal analysis on meso-fracture of concrete based on the technique of CT image processing. J Basic Sci Eng, 2012, 20(3): 424 doi: 10.3969/j.issn.1005-0930.2012.03.009田威, 黨發寧, 陳厚群. 基于CT圖像處理技術的混凝土細觀破裂分形分析. 應用基礎與工程科學學報, 2012, 20(3):424 doi: 10.3969/j.issn.1005-0930.2012.03.009 [9] Jiao C J, Li X B, Cheng C M, et al. Dynamic damage constitutive relationship of high strength concrete based on fractal theory. Explos Shock Waves, 2018, 38(4): 925焦楚杰, 李習波, 程從密, 等. 基于分形理論的高強混凝土動態損傷本構關系. 爆炸與沖擊, 2018, 38(4):925 [10] Zhang W S, Zhang J B, Li J Y, et al. Research of pore area fractal characteristic of concrete and its test method. J Build Mater, 2012, 15(3): 312 doi: 10.3969/j.issn.1007-9629.2012.03.004張文生, 張建波, 李建勇, 等. 混凝土孔隙面分形特征與測試方法研究. 建筑材料學報, 2012, 15(3):312 doi: 10.3969/j.issn.1007-9629.2012.03.004 [11] Dong Y L, Xie H P, Zhao P. Study on b value and fractal dimension Df of concrete under complete process compression. J Exp Mech, 1996, 11(3): 272董毓利, 謝和平, 趙鵬. 砼受壓全過程聲發射b值與分形維數的研究. 實驗力學, 1996, 11(3):272 [12] Wu K R, Yan A, Yao W, et al. Effect of metallic aggregate on strength and fracture properties of HPC. Cem Concr Res, 2001, 31(1): 113 doi: 10.1016/S0008-8846(00)00431-2 [13] Yan A, Wu K R, Zhang D, et al. Effect of fracture path on the fracture energy of high-strength concrete. Cem Concr Res, 2001, 31(11): 1601 doi: 10.1016/S0008-8846(01)00610-X [14] Xu Z B, Xie H P. The relation between the fractal distribution and the damage evolvement of fracture structure. J Wuhan Univ Technol, 2004, 26(10): 28 doi: 10.3321/j.issn:1671-4431.2004.10.009徐志斌, 謝和平. 斷裂構造的分形分布與其損傷演化的關系. 武漢理工大學學報, 2004, 26(10):28 doi: 10.3321/j.issn:1671-4431.2004.10.009 [15] Carpinteri A. Fractal nature of material microstructure and size effects on apparent mechanical properties. Mech Mater, 1994, 18(2): 89 doi: 10.1016/0167-6636(94)00008-5 [16] Carpinteri A, Chiaia B. Crack-resistance behavior as a consequence of sell-similar fracture topologies. Int J Fract, 1996, 76(4): 327 doi: 10.1007/BF00039781 [17] Qin Z P, Tian Y, Li G, et al. Study on fractal features of flexural performance of reinforced concrete beams strengthened with BFRP sheets. J Basic Sci Eng, 2018, 26(5): 973秦子鵬, 田艷, 李剛, 等. BFRP布加固鋼筋混凝土梁抗彎性能的分形特征研究. 應用基礎與工程科學學報, 2018, 26(5):973 [18] Zhou R Z. Fractal mechanics significance of stress field singularity at crack tip for concrete structures. J Dalian Univ Technol, 1997, 37(Suppl 1): 67周瑞忠. 混凝土結構裂紋尖端應力場奇異性的分形力學意義. 大連理工大學學報, 1997, 37(增刊 1):67 [19] Luan H Y, Fan Y F, Wang D W, et al. Study on the flexural behavior of the CFRP-reinforced concrete beam with fractal theory. Eng Mech, 2015, 32(4): 160欒海洋, 范穎芳, 王大為, 等. 基于分形理論的CFRP布增強混凝土梁抗彎性能研究. 工程力學, 2015, 32(4):160 [20] Jia N, Guo J X, Wen W Q, et al. Three-dimensional characterization of wood surface roughness with improved differential box-counting. J Northeast Forest Univ, 2019, 47(9): 76 doi: 10.3969/j.issn.1000-5382.2019.09.014賈娜, 郭佳欣, 溫濰齊, 等. 應用改進差分盒維數法對木材表面粗糙度的三維表征. 東北林業大學學報, 2019, 47(9):76 doi: 10.3969/j.issn.1000-5382.2019.09.014 [21] Chen S J, Zhang X N. Fractal characteristics of asphalt mixtures based on digital image processing technique. J Build Mater, 2013, 16(3): 451 doi: 10.3969/j.issn.1007-9629.2013.03.013陳尚江, 張肖寧. 基于數字圖像處理技術的瀝青混合料分形特性. 建筑材料學報, 2013, 16(3):451 doi: 10.3969/j.issn.1007-9629.2013.03.013 [22] Cao M S, Ren Q W, Zhai A L, et al. Experimental study on fractal characterization in damages of concrete structures. Rock Soil Mech, 2005, 26(10): 1570 doi: 10.3969/j.issn.1000-7598.2005.10.009曹茂森, 任青文, 翟愛良, 等. 混凝土結構損傷的分形特征實驗分析. 巖土力學, 2005, 26(10):1570 doi: 10.3969/j.issn.1000-7598.2005.10.009 [23] Yang S, Shao L T, Guo X X, et al. Skeleton and fractal law based image recognition algorithm for concrete crack. Chin J Sci Instrum, 2012, 33(8): 1850 doi: 10.3969/j.issn.0254-3087.2012.08.025楊松, 邵龍潭, 郭曉霞, 等. 基于骨架和分形的混凝土裂縫圖像識別算法. 儀器儀表學報, 2012, 33(8):1850 doi: 10.3969/j.issn.0254-3087.2012.08.025 [24] Liu X Y, Li W W, Liang Z P. Application to fractal theory in study on the fracture surfaces of concrete. J China Three Gorges Univ Nat Sci, 2003, 25(6): 495劉小艷, 李文偉, 梁正平. 分形理論在混凝土斷裂面研究中的應用. 三峽大學學報(自然科學版), 2003, 25(6):495 [25] Wang J A, Xie H P, Tian X Y, et al. Direct fractal measurement of fracture surfaces. J Univ Sci Technol Beijing, 1999, 21(1): 6 doi: 10.3321/j.issn:1001-053X.1999.01.002王金安, 謝和平, 田曉燕, 等. 一種新的斷裂表面分形測量方法. 北京科技大學學報, 1999, 21(1):6 doi: 10.3321/j.issn:1001-053X.1999.01.002 [26] Yan A, Wu K R, Zhang D, et al. Study on the multi-fractal characterization of fracture surface of concrete materials. J Build Mater, 2002, 5(1): 46 doi: 10.3969/j.issn.1007-9629.2002.01.009嚴安, 吳科如, 張東, 等. 混凝土材料斷裂表面的多重分形特征研究. 建筑材料學報, 2002, 5(1):46 doi: 10.3969/j.issn.1007-9629.2002.01.009 [27] Zhang Q L, Hou G T, Pan W Q, et al. Fractal study on structural fracture. J Basic Sci Eng, 2011, 19(6): 853 doi: 10.3969/j.issn.1005-0930.2011.06.001張慶蓮, 侯貴廷, 潘文慶, 等. 構造裂縫的分形研究. 應用基礎與工程科學學報, 2011, 19(6):853 doi: 10.3969/j.issn.1005-0930.2011.06.001 -
點擊查看大圖
計量
- 文章訪問數: 1369
- HTML全文瀏覽量: 584
- PDF下載量: 55
- 被引次數: 0
