Optimizing multi-objective scheduling problem of hybrid flow shop with limited buffer
-
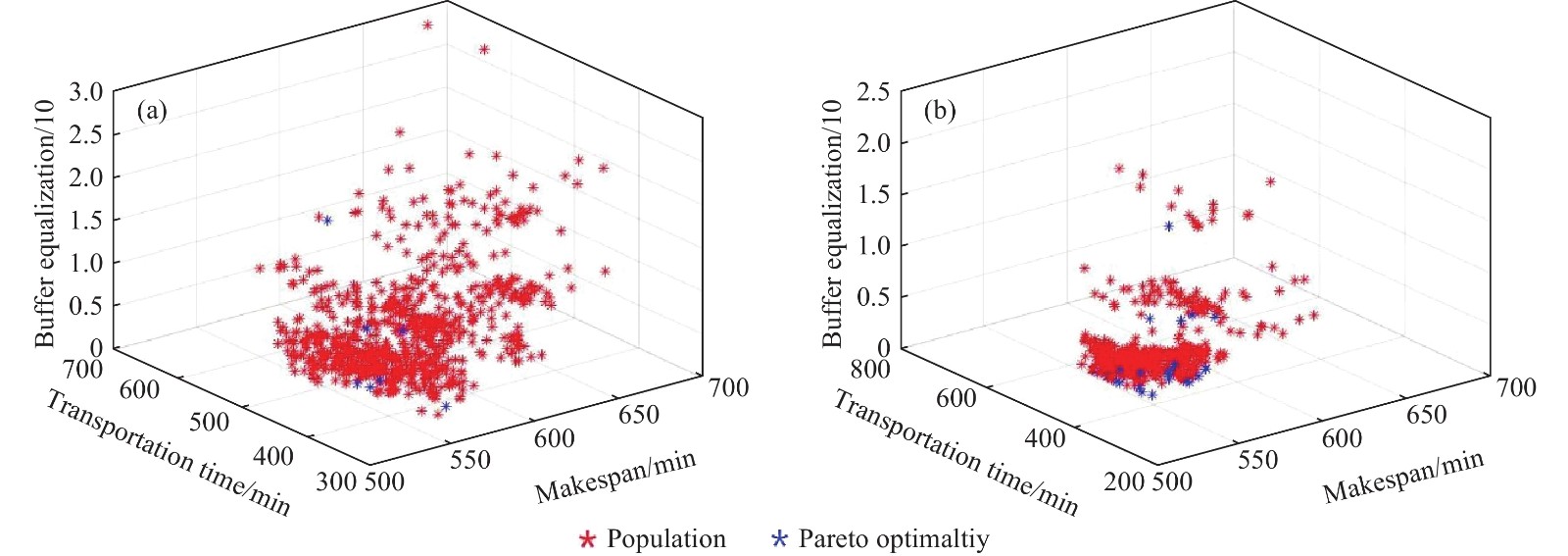
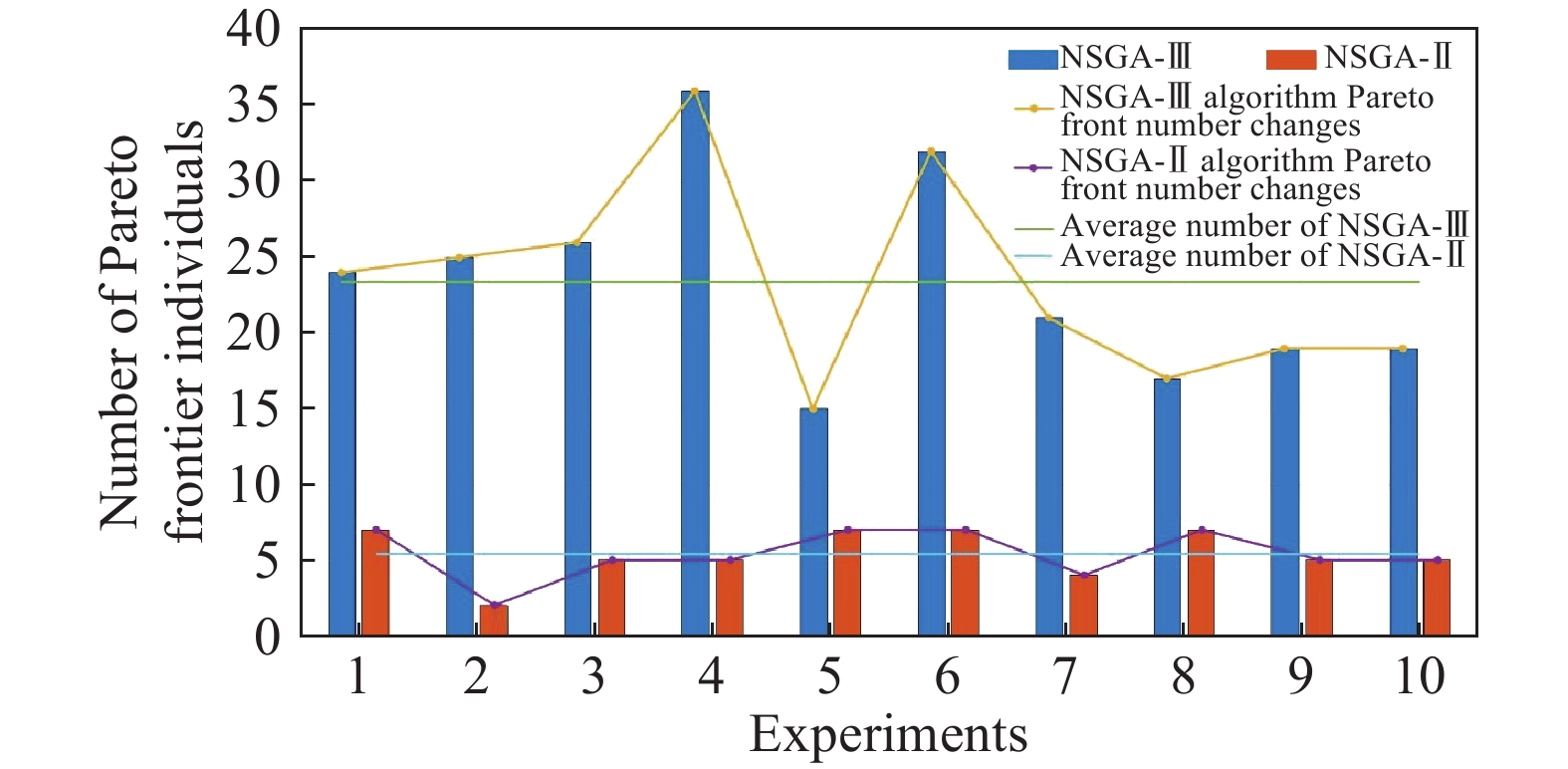
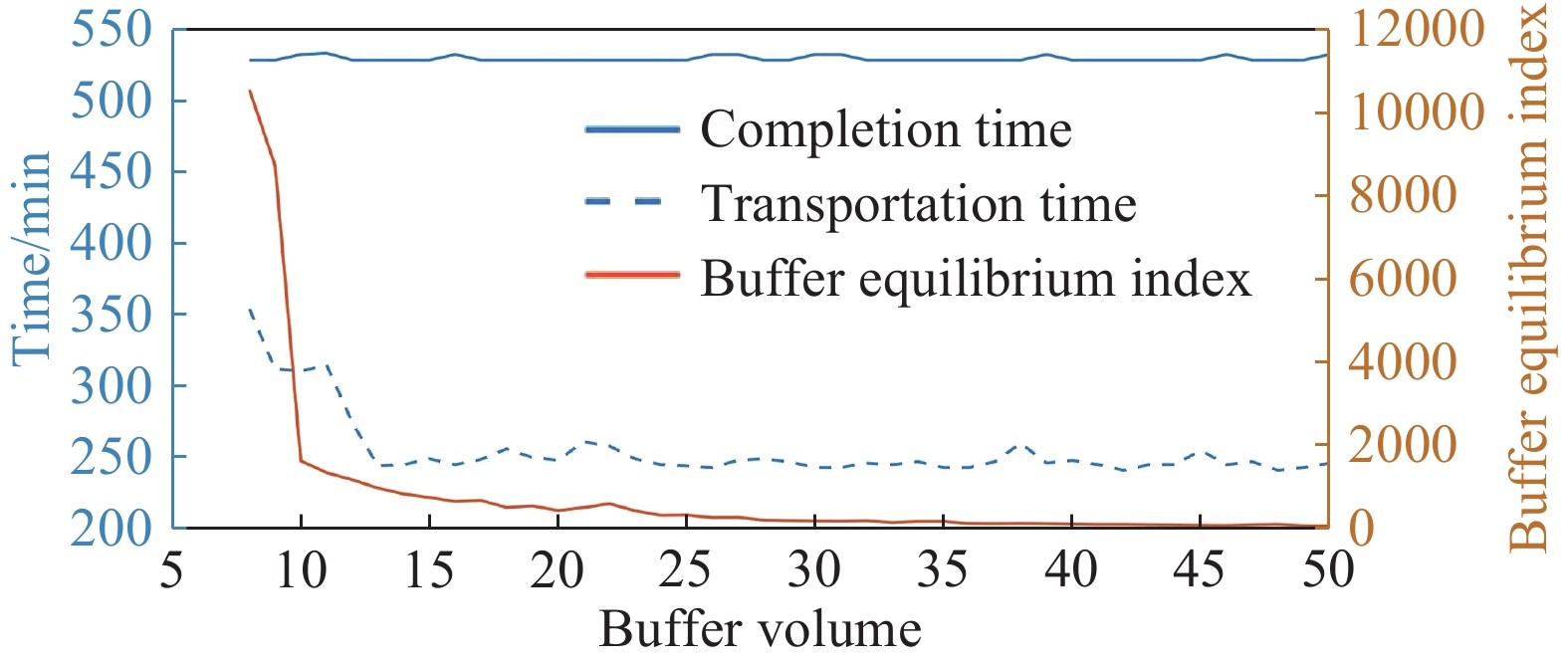
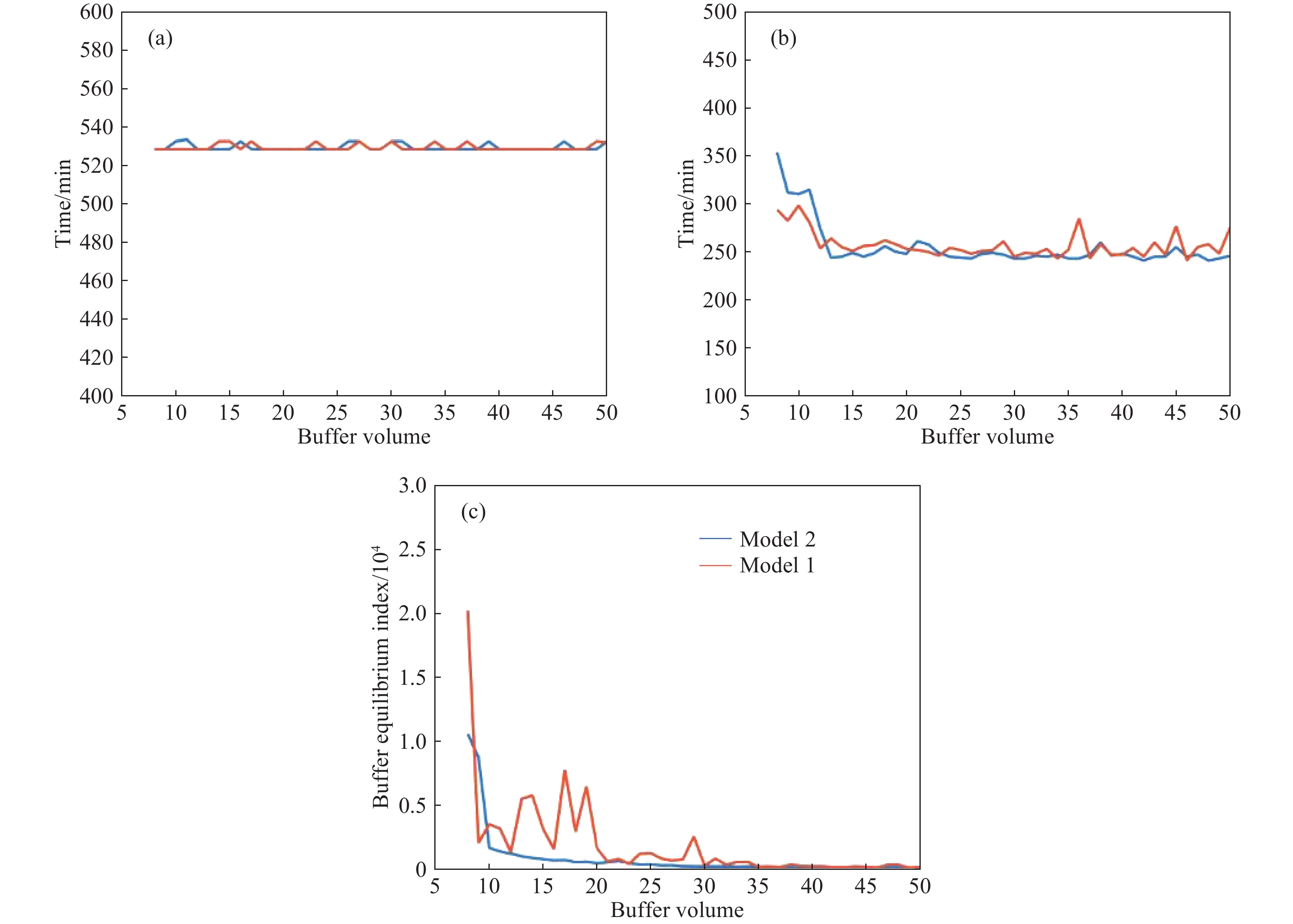
摘要: 研究對象是帶有限緩沖區混合流水車間中的多目標調度問題。以各機器前置后置緩沖區容積有限、工件以批量形式運輸、運載設備的運載能力有限等作為資源限制因素，以最小化完工時間、最小化物料運輸時間、最小化并行機前置緩沖區空間占用率均衡指數為目標，建立調度模型。分別采用NSGA-II、NSGA-III算法求解該模型，并對比兩者之間的差別；設置不同的緩沖區容積，探究不同緩沖區容積對生產目標的影響，尋找最優緩沖區容積；建立不同模型，探究以最小化并行機前置緩沖區空間占用率均衡指數為目標的意義，最后以某船用管類生產企業的實際生產案例作為對象，通過對比優化結果與實際生產數據，驗證了算法有效性。Abstract: Buffer zones in a production company are set before and after each processing equipment based on various factors such as workshop space in the hybrid-flow workshop, transportation capacity of the carrying equipment, ease of handling of the machine, machine productivity at various stages, and production cycle time. The objective of this paper was to optimizing the multi-objective scheduling problem in hybrid flow shop with limited buffer. As there was limited space (capacity) at front and rear buffers of each machine, transportation of workpieces in batches, limited carrying capacity of carrier equipment, differences in workability between parallel machines, and process determination, etc., were considered as resource limiting factors, and based upon these factors two-objective scheduling model was established with the goal of minimizing completion time and minimizing material transportation time. The two-objective scheduling model was added with minimization parallel machine front buffer space occupancy rate equilibrium index as a new goal, and established a three-objective scheduling model. In this article, NSGA-II and NSGA-III algorithms were used to solve the three-objective scheduling model, and the crossover and mutation parts of the algorithm were redesigned according to the model established. The actual production data of a marine pipe production enterprise was taken as an example and optimization results were compared with the actual production data. Thus the effectiveness of the algorithm was verified, and the difference between the two algorithms when processing the three-target scheduling model was compared, and it is concluded that NSGA-III has better convergence effect when processing the three-objective model. To explore the impact of different buffer volumes on production, target values ??under different buffer volumes were compared, and finally optimal buffer volume for each target was found out; then the two-objective model and the three-objective model were compared under different buffer volumes. The optimization results of these indicators prove the practical importance of adding the minimization of the parallel machine front buffer space occupancy rate balance index.
-
Key words:
- hybrid flow shop /
- multi-objective /
- buffer equalization /
- multi-constraint /
- NSGA-III
-
圖 3 NSGA-II（a）與NSGA-III（b）優化結果圖
Figure 3. NSGA-II (a) and NSGA-III (b) optimization results
圖 4 NSGA-II與NSGA-III一級個體數量對比圖
Figure 4. Comparison of the number of NSGA-II and NSGA-III individuals
圖 5 優化3目標有限緩沖區的混合流水車間調度模型三指標統計結果
Figure 5. Three statistical results of hybrid flow shop scheduling model with optimized three-object limited buffer zone
圖 6 模型1與模型2對比。（a）完工時間；（b）運輸時間；（c）緩沖區均衡指數
Figure 6. Comparison of model 1 and model 2: (a) completion time; (b) transportation time; (c) buffer equilibrium index
表 1 參數及變量設計
Table 1. Design of the parameters and decision variables
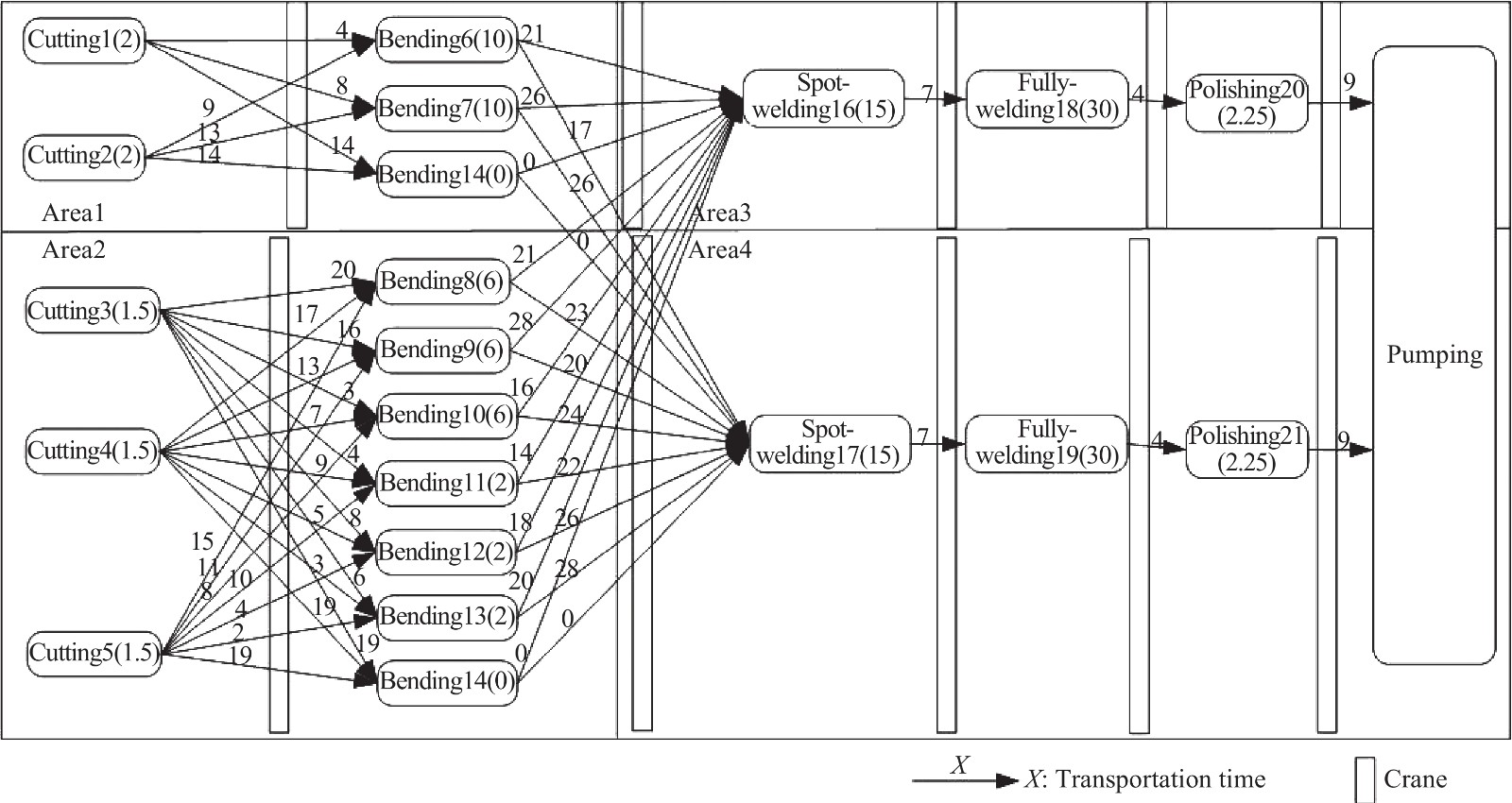
Parameters Description $C_{s,k}^{\rm{F}}$ Capacity of the kth machine’s front buffer in the stage s $C_k^{\rm{B}}$ Capacity of the kth machine’s back buffer ${N_s}$ Number of machines at the s processing stage ${J_a}$ Total number of artifacts in batch a $T_{s,k,j}^{\rm{C}}$ Completion time of job $j$ on the kth machine belong to sth stage $T_{i,s \to (s + 1),j}^{}$ Transportation completion time of ith transporter for transports job $j$ $T_{s,k,j}^{\rm{s}}$ Starting time of job $j$ that processed on the kth machine belong to sth stage $t_{_{s,k,j}}^{\rm{p}}$ The processing time of job $j$ on the kth machine belong to sth stage ${t_{i,s \to (s + 1),j}}$ The transportation time of ith transporter for transports job $j$ $T_{i,s \to (s + 1),j}^{\rm{l}}$ The leaving time of job $j$ that leaves ith transporter $T_{s,k}^{\rm{i}}$ The idle time of the kth machine belong to sth stage $T_{s,k,j}^{\rm{l}}$ The leaving time of job $j$ that leaves the kth machine belong to sth stage s $T_{s,k,{\rm{B}},j}^{\rm{l}}$ The leaving time of job $j$ that leaves back buffer of the kth machine belong to sth stage $T_{a,s,k}^{\rm{l}}$ The leaving time of ath batch that leaves the kth machine belong to sth stage $T_{i,s \to (s + 1),k}^{\rm{a}}$ The arriving time of ith transporter that arrives the kth machine belong to sth stage $V_{s,k}^{\rm{B}}$ The remaining volume of the back buffer of the kth machine belong to sth stage $V_{s,k}^{\rm{F}}$ The remaining volume of the front buffer of the kth machine belong to sth stage $T_{j,s,k}^{\rm{B}}$ The last time the back buffer of the kth machine has enough room for job $j$ $T_{(s + 1),k,a}^{\rm{F}}$ The last time the front buffer of the kth machine has enough room for batch a $T_{j,s,k}^{\rm{B}}$ The moment that the back buffer of the kth machine has enough room for job $j$ $T_{a,s,k}^{\rm{F}}$ The moment that the front buffer of the kth machine has enough room for batch a $t$ Production moment ${X_{i,s \to (s + 1),j,t}}$ If job $j$ is transported by transporter ith transporter at $t$, it is equal to 1, otherwise 0 ${X_{k,j,t}}$ If job $j$ is processed on the kth machine at $t$, it is equal to 1, otherwise 0 ${X_{j,s,k,{\rm{F}},t}}$ If job $j$ is in the front buffer of the kth machine belong to sth stage at $t$, it is equal to 1, otherwise 0 ${X_{j,k,{\rm{B}},t}}$ If job $j$ is in the back buffer of the kth machine at $t$, it is equal to 1,otherwise 0 ${X_{i,s \to (s + 1),a,t}}$ If ath transported by ith transporter t, it is equal to 1, otherwise 0 
下載: 導出CSV
表 2 工件編號以及對應各階段機器適用狀況統計表
Table 2. Workpiece number and statistics of applicable conditions of the machine at each stage
Job number Cutting Bending Spot-welding Fully-welding Polishing Pumping 1 [1,2] [6,7] [16,17] [18,19] [20,21] [22] 2 [3,4,5] [8] [16,17] [18,19] [20,21] [22] 3 [3,4,5] [9] [16,17] [18,19] [20,21] [22] 4 [3,4,5] [10] [16,17] [18,19] [20,21] [22] 5 [3,4,5] [11,12] [16,17] [18,19] [20,21] [22] 6 [3,4,5] [13] [16,17] [18,19] [20,21] [22]
下載: 導出CSV
www.77susu.com<span id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> <span id="fpn9h"><noframes id="fpn9h"> <th id="fpn9h"></th> <strike id="fpn9h"><noframes id="fpn9h"><strike id="fpn9h"></strike> <th id="fpn9h"><noframes id="fpn9h"> <span id="fpn9h"><video id="fpn9h"></video></span> <ruby id="fpn9h"></ruby> <strike id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> -
參考文獻
[1] Khosla I. The scheduling problem where multiple machines compete for a common local buffer. Eur J Oper Res, 1995, 84(2): 330 doi: 10.1016/0377-2217(93)E0352-X [2] Huang J Z, Li A P, Liu X M, et al. Optimal design of production line layout considering buffer allocation. J Tongji Univ Nat Sci, 2015, 43(7): 1075 doi: 10.11908/j.issn.0253-374x.2015.07.018黃君政, 李愛平, 劉雪梅, 等. 考慮緩沖區配置的生產線布局優化設計. 同濟大學學報(自然科學版), 2015, 43(7):1075 doi: 10.11908/j.issn.0253-374x.2015.07.018 [3] Papadopoulos H T, Vidalis M I. A heuristic algorithm for the buffer allocation in unreliable unbalanced production lines. Comput Ind Eng, 2001, 41(3): 261 doi: 10.1016/S0360-8352(01)00051-1 [4] Gupta J N D. Two-stage, hybrid flowshop scheduling problem. J Oper Res Soc, 1988, 39(4): 359 doi: 10.1057/jors.1988.63 [5] Djellab H, Djellab K. Preemptive hybrid flowshop scheduling problem of interval orders. Eur J Oper Res, 2002, 137(1): 37 doi: 10.1016/S0377-2217(01)00094-7 [6] Bolat A, Al-Harkan I, Al-Harbi B. Flow-shop scheduling for three serial stations with the last two duplicate. Comput Oper Res, 2005, 32(3): 647 doi: 10.1016/j.cor.2003.08.010 [7] Guirchoun S, Martineau P, Billaut J C. Total completion time minimization in a computer system with a server and two parallel processors. Comput Oper Res, 2005, 32(3): 599 doi: 10.1016/j.cor.2003.08.007 [8] Brah S A. A comparative analysis of due date based job sequencing rules in a flow shop with multiple processors. Prod Plan Control, 1996, 7(4): 362 doi: 10.1080/09537289608930364 [9] Brah S A, Wheeler G E. Comparison of scheduling rules in a flow shop with multiple processors: A simulation. Simulation, 1998, 71(5): 302 doi: 10.1177/003754979807100501 [10] Priya A, Sahana S K. Multiprocessor scheduling based on evolutionary technique for solving permutation flow shop problem. IEEE Access, 2020, 8: 53151 doi: 10.1109/ACCESS.2020.2973575 [11] Ruiz R, Vazquez-Rodriguez J A. The hybrid flow shop scheduling problem. Eur J Oper Res, 2010, 205(1): 1 doi: 10.1016/j.ejor.2009.09.024 [12] Khan B, Hanoun S, Johnstone M, et al. Multi-objective job shop scheduling using i-NSGA-III // 2018 Annual IEEE International Systems Conference. Vancouver, 2018: 1 [13] Li P, Yang Y X, Du X Y, et al. Iterated local search for distributed multiple assembly no-wait flowshop scheduling // 2017 IEEE Congress on Evolutionary Computation. San Sebastian, 2017 [14] Smutnicki C. A two-machine permutation flow shop scheduling problem with buffers. Oper-Res-Spektrum, 1998, 20(4): 229 doi: 10.1007/s002910050070 [15] Nowicki E. The permutation flow shop with buffers: A tabu search approach. Eur J Oper Res, 1999, 116(1): 205 doi: 10.1016/S0377-2217(98)00017-4 [16] Qian B, Wang L, Huang D X, et al. An effective hybrid DE-based algorithm for multi-objective flow shop scheduling with limited buffers. Comput Oper Res, 2009, 36(1): 209 doi: 10.1016/j.cor.2007.08.007 [17] Wang X P, Tang L X. A tabu search heuristic for the hybrid flowshop scheduling with finite intermediate buffers. Comput Oper Res, 2009, 36(3): 907 doi: 10.1016/j.cor.2007.11.004 [18] Sioud A, Gravel M, Gagne C. A genetic algorithm for solving a hybrid flexible flowshop with sequence dependent setup times // 2013 IEEE Congress on Evolutionary Computation. Cancun, 2013: 2512 [19] Omar M K. Spreadsheet approach for solving complex flowshop scheduling problems // 2011 IEEE International Conference on Industrial Engineering and Engineering Management. Singapore, 2011: 176 [20] Duan J H, Zhang M, Qiao G Y, et al. A genetic algorithm for permutation flowshop scheduling with total flowtime criterion // 2011 Chinese Control and Decision Conference (CCDC). Mianyang, 2011: 1514 [21] Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans Evol Comput, 2002, 6(2): 182 doi: 10.1109/4235.996017 [22] Wang D J, Liu F, Jin Y C. A proactive scheduling approach to steel rolling process with stochastic machine breakdown. Nat Comput, 2019, 18(4): 679 doi: 10.1007/s11047-016-9599-5 [23] Boufellouh R, Belkaid F. Multi-objective approach to optimize production and maintenance scheduling in flow shop environment under non-renewable resources constraints // 2019 International Conference on Advanced Electrical Engineering (ICAEE). Algiers, 2019 [24] Wang D J, Liu F, Wang J J, et al. Integrated rescheduling and preventive maintenance for arrival of new jobs through evolutionary multi-objective optimization. Soft Comput, 2016, 20(4): 1635 doi: 10.1007/s00500-015-1615-7 [25] Deb K, Jain H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, Part I: solving problems with box constraints. IEEE Trans Evol Comput, 2014, 18(4): 577 doi: 10.1109/TEVC.2013.2281535 -
點擊查看大圖
圖(6) / 表(2)
計量
- 文章訪問數: 1533
- HTML全文瀏覽量: 717
- PDF下載量: 87
- 被引次數: 0
