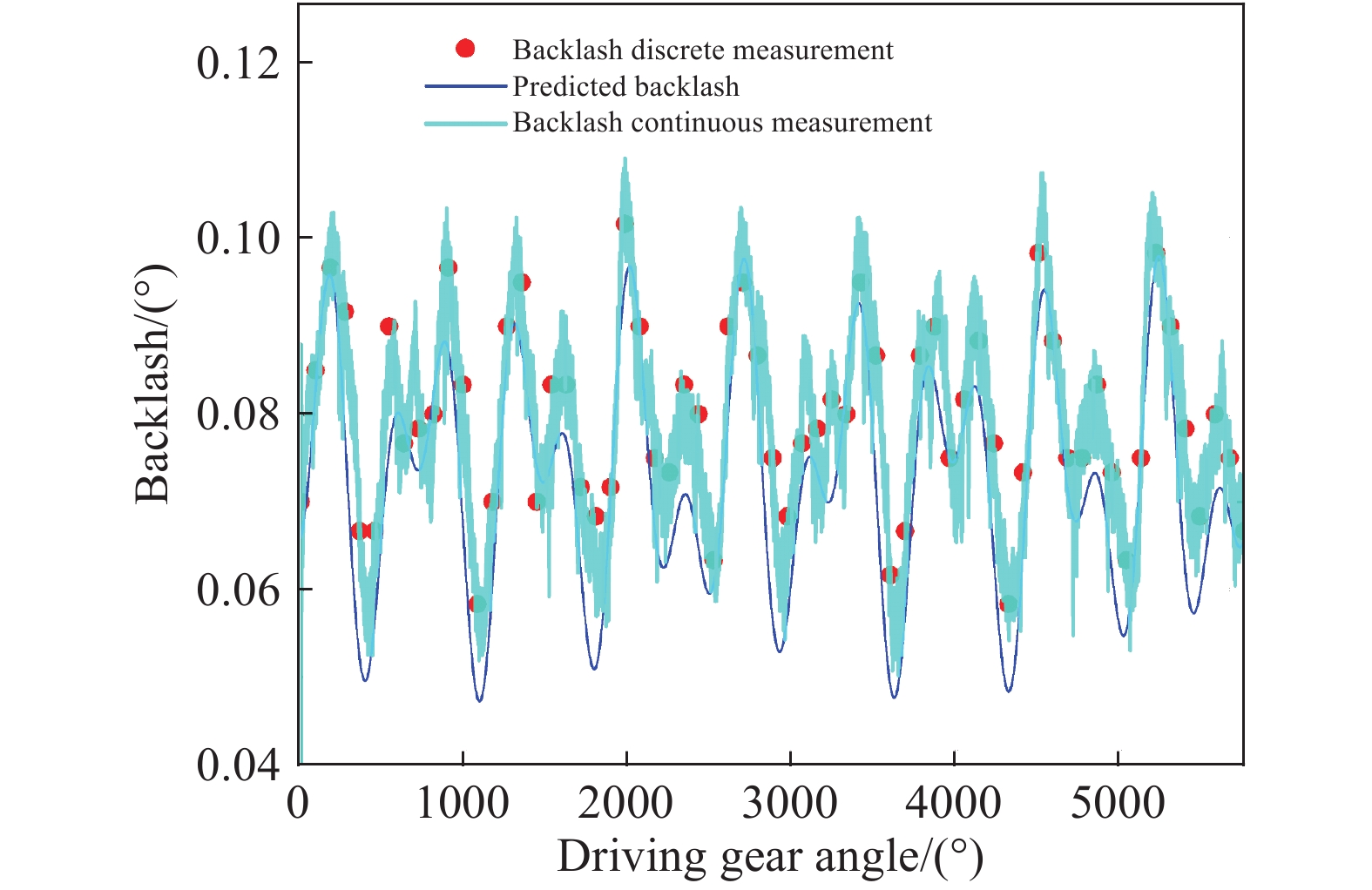
-
摘要: 提出了基于雙偏心誤差齒輪副的驅動齒面與齒背面（雙齒面）無負載傳動誤差計算模型，建立與時變側隙計算公式的等價關系，從理論上證明了基于雙齒面傳動誤差的側隙測量方法。通過實驗方法測量不同負載力矩、不同初始嚙合面的雙面傳動誤差并獲得相應載荷下的初始回差。基于雙齒面傳動誤差實驗曲線，實現了對齒輪副整個大周期側隙的連續測量與預測。結果表明，連續側隙曲線與機械滯后回差法測量結果吻合良好，而側隙預測較好地反應了側隙值變化范圍和變化趨勢。同時，側隙連續測量方法及側隙預測均證明了理論模型的正確性，提高了側隙測量效率并獲得了更全面的側隙數據，對齒輪傳動的非線性研究、消隙控制以及齒輪精度研究等均具有指導意義和參考價值。Abstract: Transmission error in gear system and backlash are important factors that affect the accuracy of precision transmission systems. The main sources of the complete cycle transmission errors and periodic backlash are eccentric errors due to imperfections in machining and assembling. Therefore, analyzing the transmission error in gear system and backlash under the effect of eccentricity error is necessary. Scholars from around the world have conducted extensive research on the transmission error of the gear system. They observed that the back-side contact of the gear tooth generally happens in high-speed light-load conditions, or when alternate load torque occurs or anti-backlash gear has been used. However, the existing literature does not evidently show the calculation method of the transmission error of the back-side tooth mesh. Therefore, analyzing the transmission error of the back-side tooth mesh is of great significance. The present work develops a calculation model of drive- and back-side (two-sided) transmission error of an involute gear pair with eccentricities to construct the equivalence of time-varying backlash calculation formula to demonstrate the continuous measurement of gear backlash based on two-sided transmission error that can also be realized in theory. The experimental transmission error and the corresponding hysteresis were acquired under various load torques and different initial conditions, such as initial position of the gear unit. The continuous backlash curve of the gear pair was obtained from the two-sided transmission curves, and the backlash of the whole cycle could be predicted. The result of the experiment shows that the continuous measurement curve agrees with the mechanical hysteresis method, and the prediction of backlash perfectly reflects the variation range and trend of backlash. Moreover, both the continuous measurement method of backlash and prediction of backlash demonstrate that the model is practicable and have higher efficiency, and the overall data retain instructional significance, reference value for nonlinear research, anti-backlash control, and gear accuracy of gear transmission.
-
圖 1 主動輪偏心誤差下嚙合線增量計算模型。（a）嚙合齒面為驅動齒面；（b）嚙合齒面為齒背面
Figure 1. Engagement increment calculation model with eccentric error of pinion: (a) drive-side meshing; (b) back-side meshing
圖 2 從動輪偏心誤差下嚙合線增量計算模型。（a）嚙合齒面為驅動齒面；（b）嚙合齒面為齒背面
Figure 2. Engagement increment calculation model with eccentric error of driven gear: (a) drive-side meshing; (b) back-side meshing
圖 3 傳動誤差及側隙測量實驗裝置圖
Figure 3. Experimental device for transmission error and backlash measurement
圖 4 驅動齒面傳動誤差測量起始位置示意圖。（a）初始接觸齒面為驅動齒面；（b）初始接觸齒面為齒背面
Figure 4. Schematic of the initial position of the drive-side transmission error measurement: (a) drive-side contact in initial position; (b) back-side contact in initial position
圖 5 齒背面傳動誤差測量起始位置示意圖。（a）初始接觸齒面為驅動齒面；（b）初始接觸齒面為齒背面
Figure 5. Schematic of the initial position of the back-side transmission error measurement: (a) drive-side contact in initial position; (b) back-side contact in initial position
圖 6 驅動齒面傳動誤差測量且初始時刻驅動齒面接觸。（a）傳動誤差對比曲線；（b）各負載與其初始回差對比
Figure 6. Drive-side transmission error measurement with drive-side contact at initial position: (a) comparison of transmission error curves; (b) comparison of each load torque with its corresponding hysteresis
圖 7 驅動齒面傳動誤差測量且初始時刻齒背面接觸。（a）傳動誤差對比曲線；（b）各負載與其初始回差對比
Figure 7. Drive-side transmission error measurement with back-side contact at initial position: (a) comparison of transmission error curves; (b) comparison of each load torque with its corresponding hysteresis
圖 8 齒背面傳動誤差測量且初始時刻驅動齒面接觸。（a）傳動誤差對比曲線；（b）各負載與其初始回差對比
Figure 8. Back-side transmission error measurement with drive-side contact at initial position: (a) comparison of transmission error curves; (b) comparison of each load torque with its corresponding hysteresis
圖 9 齒背面傳動誤差測量且初始時刻齒背面接觸。（a）傳動誤差對比曲線；（b）各負載與其初始回差對比
Figure 9. Back-side transmission error measurement with back-side contact at initial position: (a) comparison of transmission error curves; (b) comparison of each load torque with its corresponding hysteresis.
圖 10 雙面傳動誤差與側隙連續曲線
Figure 10. Two-sided transmission error and continuous backlash curve
圖 11 齒背面傳動誤差實驗及擬合曲線
Figure 11. Experimental and fitting curve of back-side transmission error
圖 13 機械滯后回差法測量原理
Figure 13. Measurement principle of mechanical return backlash method
表 1 齒輪副基本參數
Table 1. Basic parameters of gear pair
System parameters Value Tooth number of driving gear 45 Tooth number of driven gear 80 Module/mm 2 Pressure angle/(°) 20 Tooth width/mm 20 Addendum circle diameter of driving gear/mm 94 Dedendum circle diameter of driving gear/mm 85 Addendum circle diameter of driven gear/mm 164 Dedendum circle diameter of driven gear/mm 155 Driving speed/(r·min?1) 10 Loading torque/(N?m) 0 2.5 5 7.5 10 
下載: 導出CSV
表 2 各部分理論剛度
Table 2. Theoretical stiffness of each part
Part Theoretical stiffness Gear 20 N?(μm?mm)?1 Shaft 289.44 N?m?(°)?1 Spline 9.768×107?P1/3 N?m?1 Coupling 1.87×104 N?m?rad?1
下載: 導出CSV
表 3 不同負載力矩下，各部分變形數據
Table 3. Deformation data of various parts under different loads
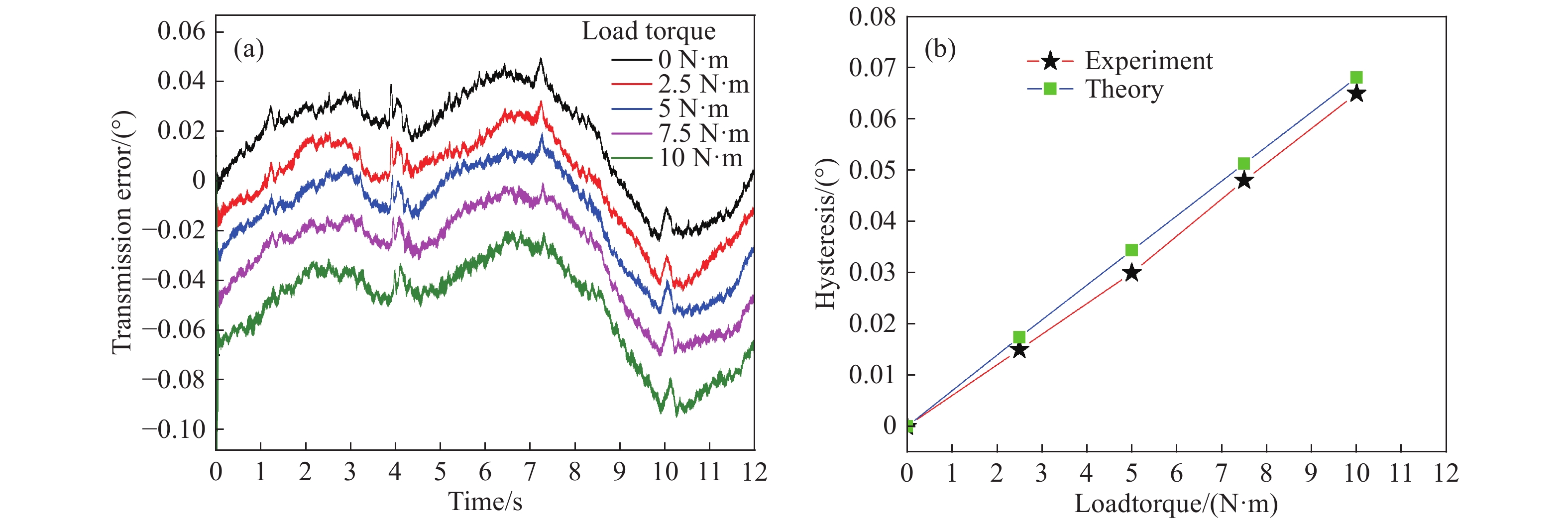
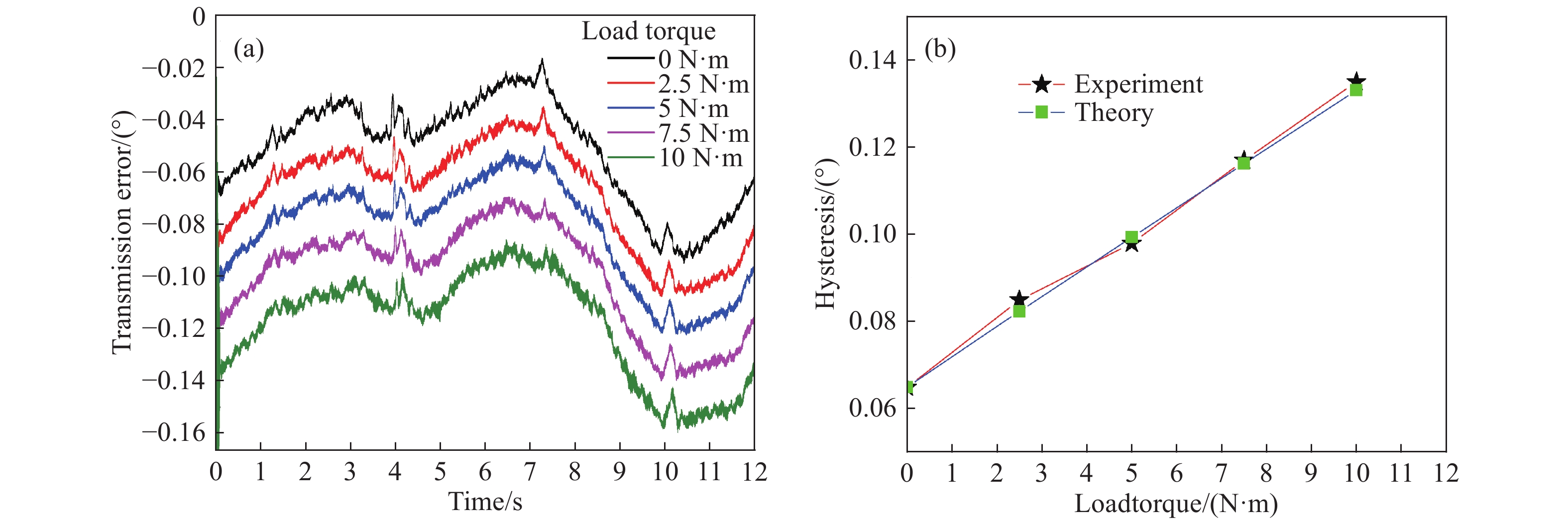
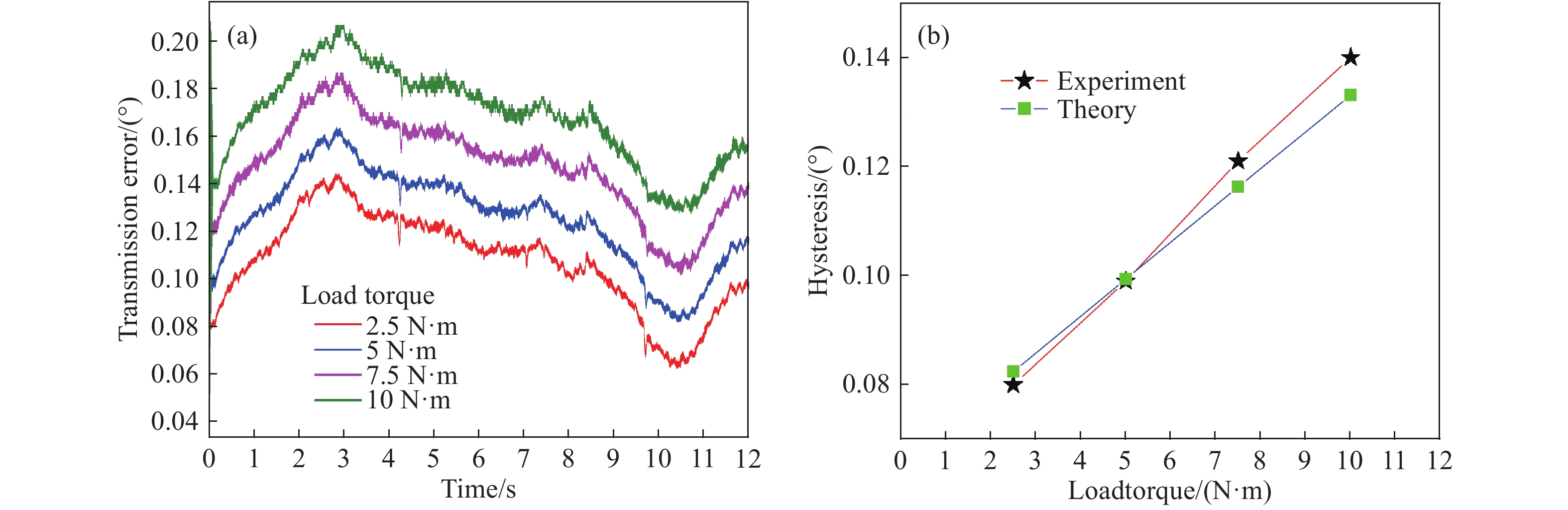
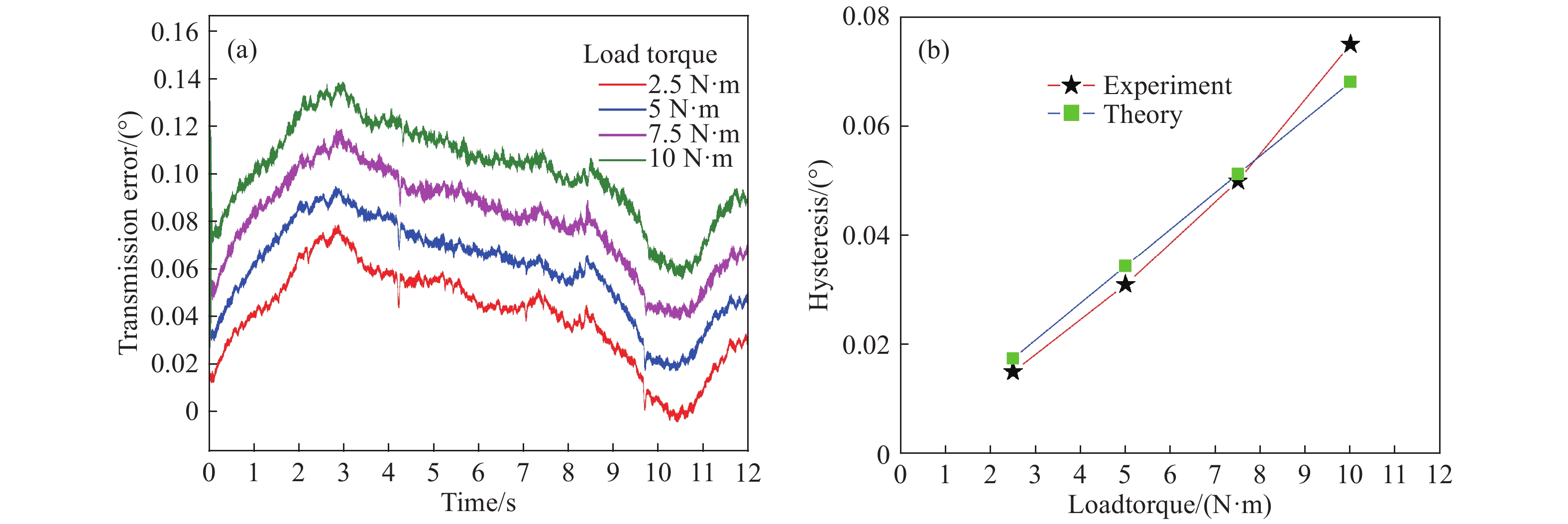
Part Theoretical deformation/(10?3 °) 2.5 N?m 5 N?m 7.5 N?m 10 N?m Gear 0.06 0.11 0.17 0.22 Shaft 8.64 17.27 25.91 34.55 Spline 1.06 1.69 2.21 2.68 Coupling 7.66 15.32 22.98 30.64 Theoretical total deformation 17.42 34.39 51.27 68.09 Experimental total deformation Drive-side 15 30 48 65 Back-side 15 31 50 75
下載: 導出CSV
www.77susu.com<span id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> <span id="fpn9h"><noframes id="fpn9h"> <th id="fpn9h"></th> <strike id="fpn9h"><noframes id="fpn9h"><strike id="fpn9h"></strike> <th id="fpn9h"><noframes id="fpn9h"> <span id="fpn9h"><video id="fpn9h"></video></span> <ruby id="fpn9h"></ruby> <strike id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> -
參考文獻
[1] Wang G J, Chen L, Yu L, et al. Research on the dynamic transmission error of a spur gear pair with eccentricities by finite element method. <italic>Mech Mach Theory</italic>, 2017, 109: 1 doi: 10.1016/j.mechmachtheory.2016.11.006 [2] Yu L, Wang G J, Zou S D. The calculation of meshing efficiency of a new type of conical involute gear. <italic>Strojni?ki vestnik-J Mech Eng</italic>, 2017, 63(5): 320 doi: 10.5545/sv-jme.2016.3843 [3] Zou S D, Wang G J, Yu L. Research on calculation of unloaded transmission error of planetary gear train caused by eccentricity // ASME 2017International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Cleveland, 2017: 1 [4] Michalec G W. Precision Gearing: Theory and Practice. New York: Wiley, 1966 [5] Wu C S. The turning angle error from gears eccentric error. <italic>J Nanjing Inst Technol</italic>, 1982(4): 133吳慈生. 齒輪偏心誤差所引起的傳動誤差. 南京工學院學報, 1982(4):133 [6] Zou S D, Wang G J. Research on transmission error of dual-eccentric gears. <italic>J Univ Electron Sci Technol China</italic>, 2017, 46(6): 955 doi: 10.3969/j.issn.1001-0548.2017.06.027鄒帥東, 王光建. 雙齒輪偏心的傳動誤差計算與研究. 電子科技大學學報, 2017, 46(6):955 doi: 10.3969/j.issn.1001-0548.2017.06.027 [7] Yu L, Wang G J, Zou S D. The experimental research on gear eccentricity error of backlash-compensation gear device based on transmission error. <italic>Int J Precis Eng Manuf</italic>, 2018, 19(1): 5 doi: 10.1007/s12541-018-0001-7 [8] Wang C B, Chen X A, Chen H, et al. Influence of error's randomness on transmission accuracy of planetary gear. <italic>J Chongqing Univ</italic>, 2012, 35(9): 41王朝兵, 陳小安, 陳宏, 等. 誤差隨機性對行星齒輪系傳動精度的影響特性. 重慶大學學報, 2012, 35(9):41 [9] Guo Y, Parker R G. Dynamic modeling and analysis of a spur planetary gear involving tooth wedging and bearing clearance nonlinearity. <italic>Eur J Mech-A/Solids</italic>, 2010, 29(6): 1022 doi: 10.1016/j.euromechsol.2010.05.001 [10] Guo Y C, Parker R G. Analytical determination of back-side contact gear mesh stiffness. <italic>Mech Mach Theory</italic>, 2014, 78: 263 doi: 10.1016/j.mechmachtheory.2014.03.011 [11] Yu W N, Mechefske C K, Timusk M. Influence of the addendum modification on spur gear back-side mesh stiffness and dynamics. <italic>J Sound Vib</italic>, 2017, 389: 183 doi: 10.1016/j.jsv.2016.11.030 [12] Shi J F, Gou X F, Zhu L Y. Modeling and analysis of a spur gear pair considering multi-state mesh with time-varying parameters and backlash. <italic>Mech Mach Theory</italic>, 2019, 134: 582 doi: 10.1016/j.mechmachtheory.2019.01.018 [13] Raghuwanshi N K, Parey A. Effect of back-side contact on mesh stiffness of spur gear pair by finite element method. <italic>Procedia Eng</italic>, 2017, 173: 1538 doi: 10.1016/j.proeng.2016.12.239 [14] Shi Z G, Zuo Z Y. Backstepping control for gear transmission servo systems with backlash nonlinearity. <italic>IEEE Trans Autom Sci Eng</italic>, 2015, 12(2): 752 doi: 10.1109/TASE.2014.2369430 [15] Li X P, Mu J X, Pan W J, et al. Influence of fractal backlash on dynamic behavior of gear-bearing system. <italic>J Mech Eng</italic>, 2018, 54(9): 153李小彭, 牟佳信, 潘五九, 等. 具有分形特性的齒側間隙對齒輪-軸承系統動態特性的影響. 機械工程學報, 2018, 54(9):153 [16] Chen Q, Ma Y B, Huang S W, et al. Research on gears’ dynamic performance influenced by gear backlash based on fractal theory. <italic>Appl Surf Sci</italic>, 2014, 313: 325 doi: 10.1016/j.apsusc.2014.05.210 [17] Yi Y, Huang K, Xiong Y S, et al. Nonlinear dynamic modelling and analysis for a spur gear system with time-varying pressure angle and gear backlash. <italic>Mech Syst Signal Process</italic>, 2019, 132: 18 doi: 10.1016/j.ymssp.2019.06.013 [18] Jin G H, Long S S, Gao P, et al. Load sharing characteristics and experimental research of cylindrical gear split-torque transmission system. <italic>J Central S Univ Sci Technol</italic>, 2019, 50(7): 1592靳廣虎, 龍珊珊, 高鵬, 等. 圓柱齒輪分扭傳動系統的均載特性及試驗研究. 中南大學學報: 自然科學版, 2019, 50(7):1592 [19] Gui Y F, Zhu R P, Jin G H, et al. Dynamic and load sharing characteristic analysis of a nonlinear cylindrical gear split-torque transmission system with backlash. <italic>J Vib Shock</italic>, 2014, 33(18): 177桂永方, 朱如鵬, 靳廣虎, 等. 間隙非線性圓柱齒輪分流傳動系統動力學與均載特性分析. 振動與沖擊, 2014, 33(18):177 [20] Gear manual editorial board. Gear Manual. 2nd Ed. Beijing: China Machine Press, 2006齒輪手冊編委會. 齒輪手冊. 2版. 北京: 機械工業出版社, 2006 [21] Chen L. Simulation on the Dynamic Transmission Error of a New Type of Variable Tooth Thickness Gear System with Eccentric Gears[Dissertation]. Chongqing: Chongqing University, 2015陳林. 偏心激勵下新型變齒厚齒輪系統動態傳動誤差仿真研究[學位論文]. 重慶: 重慶大學, 2015 [22] Yu L, Wang G J, He L L. The electrically controlling anti-backlash based on variable tooth thickness gear // <italic>The International Conference on Gears</italic>. <italic>Munich</italic>, 2015: 591 [23] Yang Z. Study on Precision Assembly Key Parameters and Its Effects on Dynamics Performance of Anti-Backlash Gear System[Dissertation]. Changsha: National University of Defense Technology, 2014楊政. 消隙齒輪系統精密裝配關鍵參數及其動力學性能影響研究[學位論文]. 長沙: 國防科學技術大學, 2014 [24] Yu L. The Research on Backlash Control Based on New Type of Conical Involute Gear [Dissertation]. Chongqing: Chongqing University, 2017喻立. 新型變齒厚齒輪側隙控制方法研究[學位論文]. 重慶: 重慶大學, 2017 [25] Cheng D X. Handbook of Mechanical Design. 6th Ed. Beijing: Chemical Industry Press, 2016成大先. 機械設計手冊. 6版. 北京: 化學工業出版社, 2016 [26] Gu B Z, Zhou Y M, Yang D H. Stiffness calculation and application of spline-ball bearing. <italic>Astron Res Technol</italic>, 2006, 3(4): 365顧伯忠, 周于鳴, 楊德華. 滾珠花鍵副的剛度的計算及應用. 天文研究與技術, 2006, 3(4):365 -
點擊查看大圖
計量
- 文章訪問數: 1390
- HTML全文瀏覽量: 908
- PDF下載量: 35
- 被引次數: 0
