An improved Bouc –Wen model for describing hysteretic characteristics of shock absorbers
-
摘要: Bouc–Wen模型在非識別激勵工況下模擬的阻尼力與實際阻尼力誤差較大，對非識別激勵振幅過于敏感，針對這一問題，提出了一種描述減振器滯回特性的改進模型。首先用Mechanical testing and simulation(MTS)疲勞試驗機對磁流變減振器進行力學性能試驗，獲得在多種激勵幅值、頻率和電流作用下的阻尼力。采用阻尼力對位移的斜率與阻尼力關系來模擬滯回環特性曲線。根據滯回曲線特點利用二次多項式函數來表征滯回環斜率與阻尼力的關系，同時，引入關于速度的指數函數修正項，進而對改進后的Bouc–Wen模型進行參數識別，并對其進行仿真及驗證。與試驗得到的阻尼力進行對比，發現在非識別激勵工況下，曲線吻合效果較好。對改進前后Bouc–Wen模型模擬的阻尼力特性曲線進行對比，結果表明：改進后模型得到的阻尼力仿真值能夠較好地模擬試驗得到的各種工況下阻尼力的值，且優于Bouc–Wen模型，同時Bouc–Wen模型在非識別激勵工況下模擬阻尼力精度較差這一問題得到了改善。新模型為保證車輛懸架系統在多變工況下仿真響應的準確性打下了基礎。Abstract: The error between the actual damping force and the simulated damping force obtained using the Bouc–Wen model under non-identification excitation conditions is large, and the model is too sensitive to non-identification excitation amplitude and thus features poor accuracy. To solve this sensitivity problem, an improved model describing hysteretic characteristics of shock absorbers was proposed. Firstly, the mechanical properties of a magnetorheological (MR) damper were tested to obtain the damping force under various excitation amplitudes, frequencies and currents using a mechanical testing and simulation(MTS) fatigue testing machine. The smooth hysteresis loop curve was simulated based on the relationship between the slope of the hysteresis loop and the damping force. The quadratic polynomial function was used to characterize the relationship between the slope of hysteresis loop and the damping force according to the hysteresis curve characteristics. At the same time, the revision term of the exponential function for the velocity value was introduced, and the parameters of the established improved Simulink model were identified. The damping forces under different working conditions were obtained from the experiment, and the new model was simulated and validated. The damping forces obtained from new model and the experiment were compared, and the curves obtained from the model agree well with the experimental results under different working conditions. Meanwhile, the improved model was compared with the Bouc–Wen model based on the characteristic curves of the damping force. The results show that the improved model can better simulate the damping force values obtained from tests under different conditions, and is superior to the Bouc–Wen model. At the same time, the problem of poor accuracy of the Bouc–Wen model under non identification excitation conditions was improved. The new model lays the foundation for ensuring the accuracy of the vehicle suspension system response under various working conditions.
-
圖 6 識別參數擬合曲線。（a） c0；（b） k0；（c） b；（d） α
Figure 6. Identification parameter fitting curve：(a) c0; (b) k0; (c) b; (d) α
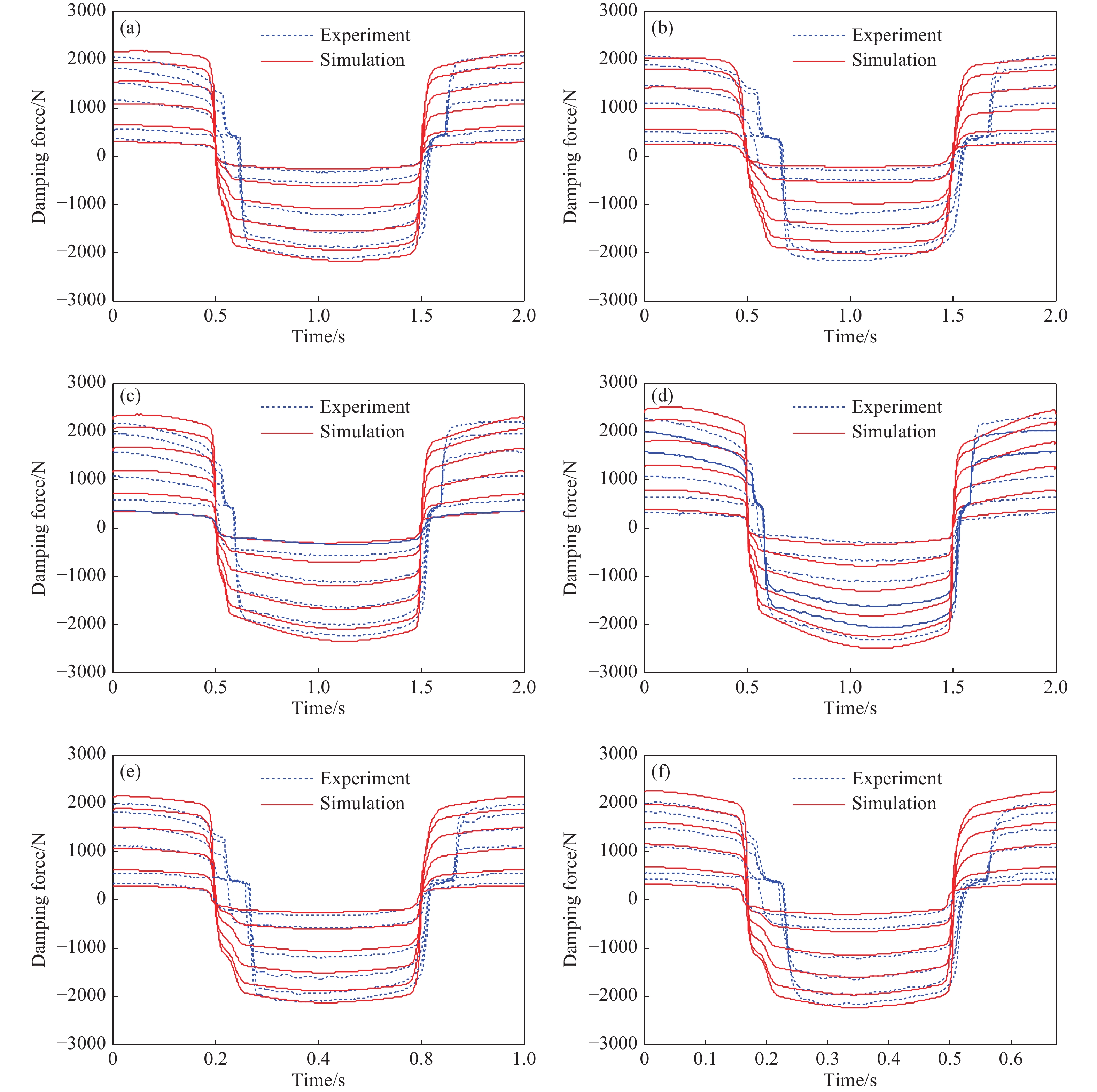
圖 8 不同工況下的試驗值與仿真值時域對比圖。（a） 10 mm，0.5 Hz；（b） 5 mm，0.5 Hz；(c) 15 mm，0.5 Hz；（d） 20 mm，0.5 Hz；（e） 5 mm，1.0 Hz；（f） 5 mm，1.5 Hz
Figure 8. Comparison diagram of test value and simulation value under different working conditions: (a) 10 mm, 0.5 Hz; (b) 5 mm, 0.5 Hz; (c) 15 mm, 0.5 Hz; (d) 20 mm,0.5 Hz; (e) 5 mm, 1.0 Hz; (f) 5 mm, 1.5 Hz
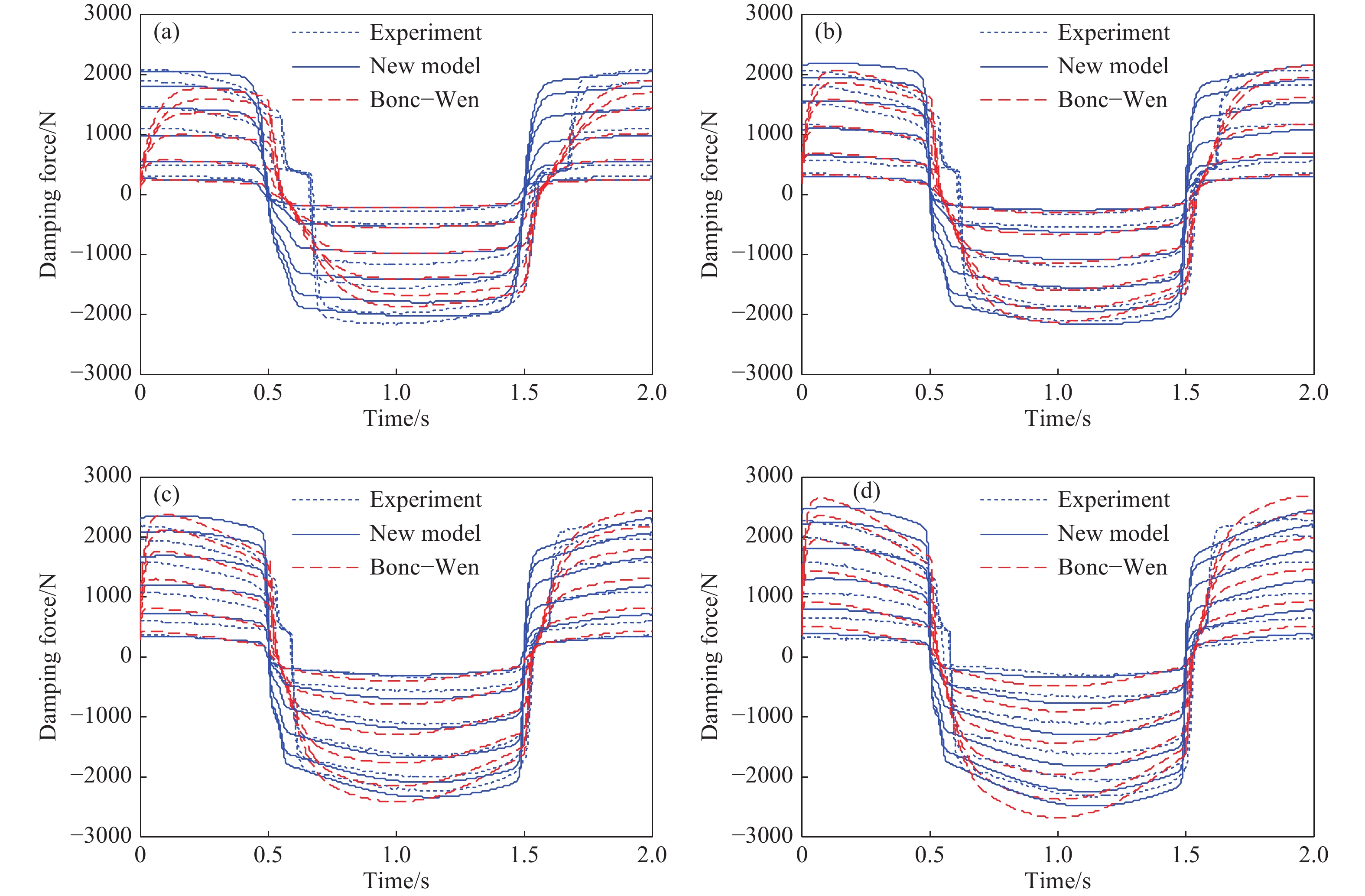
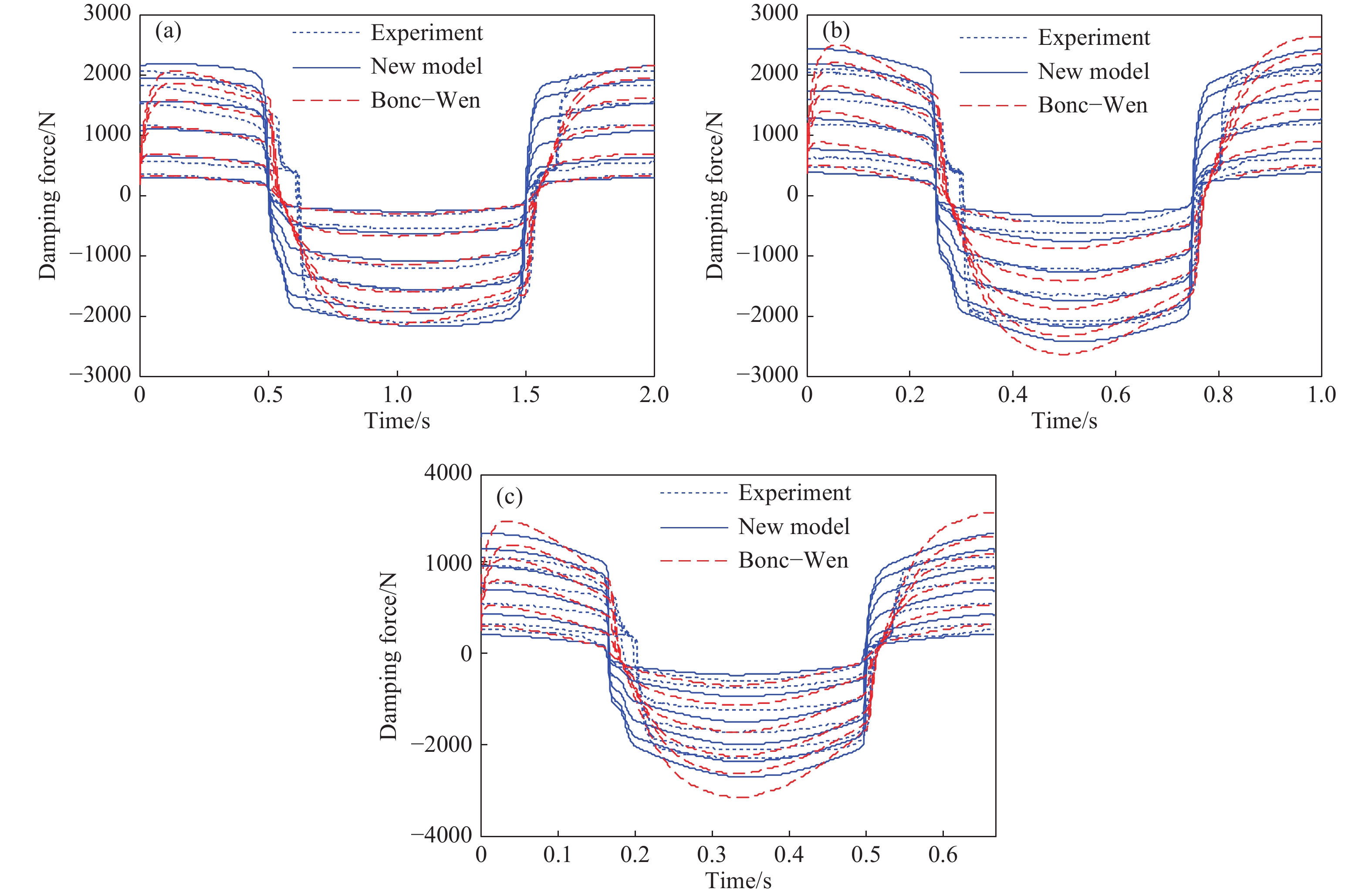
圖 9 多種工況下的試驗與仿真滯回特性對比圖。（a）10 mm，0.5 Hz；（b）5 mm，0.5 Hz；（c）15 mm，0.5 Hz；（d）20 mm，0.5 Hz；(e）5 mm，1.0 Hz；（f）5 mm，1.5 Hz
Figure 9. Comparison of hysteretic characteristics between test and simulation under various working conditions: (a) 10 mm, 0.5 Hz; (b) 5 mm, 0.5 Hz; (c) 15 mm, 0.5 Hz; (d) 20 mm, 0.5 Hz; (e) 5 mm, 1.0 Hz; (f) 5 mm, 1.5 Hz
圖 10 不同幅值相同頻率的對比圖。（a） 5 mm，0.5 Hz；（b） 10 mm，0.5 Hz；（c） 15 mm，0.5 Hz；（d） 20 mm，0.5 Hz
Figure 10. Comparison of fixed frequencies and different amplitudes: (a) 5 mm, 0.5 Hz; (b) 10 mm, 0.5 Hz; (c) 15 mm, 0.5 Hz; (d) 20 mm, 0.5 Hz
圖 11 相同幅值不同頻率的對比圖。（a）10 mm，0.5 Hz；（b）10 mm，1.0 Hz；（c）10 mm，1.5 Hz
Figure 11. Comparison of fixed amplitude and different frequencies: (a) 10 mm, 0.5 Hz; (b) 10 mm, 1.0 Hz; (c) 10 mm, 1.5 Hz
表 1 部分工況下改進前與改進后模型的偏差對比
Table 1. Comparison of the deviations between the improved model and Bouc–Wen model under some conditions
Current/A 5 mm, 0.5 Hz 20 mm, 0.5 Hz 10 mm, 1.0 Hz 10 mm, 1.5 Hz Bouc–Wen New model Bouc–Wen New model Bouc–Wen New model Bouc–Wen New model 0 0.2004 0.1987 0.5608 0.1336 0.0853 0.2133 0.1921 0.2117 0.5 0.1318 0.1041 0.3714 0.1827 0.4058 0.2139 0.5559 0.2749 1.0 0.1188 0.1403 0.3215 0.1944 0.1785 0.0549 0.4553 0.2562 1.5 0.0659 0.0578 0.2237 0.1306 0.1587 0.0665 0.3445 0.1888 2.0 0.1283 0.0722 0.1652 0.0966 0.1316 0.0568 0.2855 0.1564 2.5 0.1153 0.0406 0.1620 0.0806 0.2411 0.1428 0.4156 0.2139 
下載: 導出CSV
www.77susu.com<span id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> <span id="fpn9h"><noframes id="fpn9h"> <th id="fpn9h"></th> <strike id="fpn9h"><noframes id="fpn9h"><strike id="fpn9h"></strike> <th id="fpn9h"><noframes id="fpn9h"> <span id="fpn9h"><video id="fpn9h"></video></span> <ruby id="fpn9h"></ruby> <strike id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> -
參考文獻
[1] Zheng S H, Lin S W. Research on the nonlinear hysteretic response characteristics of intelligent vibratory roller under horizontal excitation mode. Adv Mater Res, 2013, 694-697: 2964 doi: 10.4028/www.scientific.net/AMR.694-697.2964 [2] Zhang Y M, Fu L Y, Wen B C. Vibration analysis of uncertain single-degree-of-freedom hysteretic system. J Vib Eng, 2004, 17(1): 11張義民, 付立英, 聞邦椿. 單自由度隨機滯回系統的振動響應分析. 振動工程學報, 2004, 17(1):11 [3] Shen P H, Lin S W. Mathematic modeling and characteristic analysis for dynamic system with asymmetrical hysteresis in vibratory compaction. Meccanica, 2008, 43(5): 505 doi: 10.1007/s11012-008-9114-x [4] Peng H, Zhang J Q, Liu Y L, et al. MR damper’s modeling based on improved dual-sigmoid model. J Vib Shock, 2019, 38(15): 216彭虎, 張進秋, 劉義樂, 等. 基于改進雙Sigmoid模型的磁流變減振器力學建模研究. 振動與沖擊, 2019, 38(15):216 [5] Khan M S A, Suresh A, Ramaiah N S. Numerical study of magnetic circuit response in magneto-rheological damper. J Eng Des Technol, 2016, 14(1): 196 [6] Yu H J, Sun X T, Xu J, et al. The time-delay coupling nonlinear effect in sky-hook control of vibration isolation systems using Magneto-Rheological Fluid dampers. J Mech Sci Technol, 2016, 30(9): 4157 doi: 10.1007/s12206-016-0827-9 [7] Dutta S, Chakraborty G. Performance analysis of nonlinear vibration isolator with magneto-rheological damper. J Sound Vib, 2014, 333(20): 5097 doi: 10.1016/j.jsv.2014.05.028 [8] Wen Y K. Equivalent linearization for hysteretic systems under random excitation. J Appl Mech, 1980, 47(1): 150 doi: 10.1115/1.3153594 [9] Peng Z L, Zhou C G. Research on modeling of nonlinear vibration isolation system based on Bouc–Wen model. Defence Technol, 2014, 10(4): 371 doi: 10.1016/j.dt.2014.08.001 [10] Stanway R, Sproston J L, Stevens N G. Non-linear modelling of an electro-rheological vibration damper. J Electrostatics, 1987, 20(2): 167 doi: 10.1016/0304-3886(87)90056-8 [11] Guneyisi E, Gesoglu M, Naji N, et al. Evaluation of the rheological behavior of fresh self-compacting rubberized concrete by using the Herschel–Bulkley and modified Bingham models. Arch Civil Mech Eng, 2016, 16(1): 9 doi: 10.1016/j.acme.2015.09.003 [12] Jeong S W. Determining the viscosity and yield surface of marine sediments using modified Bingham models. Geosciences J, 2013, 17(3): 241 doi: 10.1007/s12303-013-0038-7 [13] Turnip A, Hong K S, Park S. Control of a semi-active MR-damper suspension system: A new polynomial model. IFAC Proc Volumes, 2008, 41(2): 4683 doi: 10.3182/20080706-5-KR-1001.00788 [14] Duan M, Su H H. Polynomial model research on automobiles magneto-rheological damper. J Liaoning Inst Technol Nat Sci Ed, 2010, 30(6): 377段敏, 蘇海華. 汽車磁流變減振器多項式模型的研究. 遼寧工業大學學報: 自然科學版, 2010, 30(6):377 [15] Lau Y K, Liao W H. Design and analysis of magnetorheological dampers for train suspension. Proc Inst Mech Eng Part F J Rail Rapid Transit, 2005, 219(4): 261 doi: 10.1243/095440905X8899 [16] Peng G R, Li W H, Du H, et al. Modelling and identifying the parameters of a magneto rheological damper with a force-lag phenomenon. Appl Math Model, 2014, 38(15-16): 3763 doi: 10.1016/j.apm.2013.12.006 [17] Wang W R, Wu C, Chen Y, et al. Modified Bouc–Wen model based on hysteretic characteristics experiment of magneto-rheological damper. Trans Chin Soc Agric Machinery, 2011, 42(2): 48王維銳, 吳參, 陳穎, 等. 磁流變減振器滯回特性的改進Bouc–Wen模型. 農業機械學報, 2011, 42(2):48 [18] Zhong G Q, Zhou Y, Li L J, et al. Parameter identification of BRB based on improved Bouc–Wen model using GSO algorithm. J Building Struct, 2018, 39(Suppl1): 387鐘根全, 周云, 李麗娟, 等. 基于GSO算法的BRB改進Bouc–Wen模型參數識別. 建筑結構學報, 2018, 39(增刊1): 387 [19] Yao G Z, Yap F F, Chen G, et al. MR damper and its application for semi-active control of vehicle suspension system. Mechatronics, 2002, 12(7): 963 doi: 10.1016/S0957-4158(01)00032-0 [20] Liu Y Q, Yang S P, Liao Y Y. A new method of parameter identification for magnetorheological damper model. J Mech Eng, 2018, 54(6): 62 doi: 10.3901/JME.2018.06.062劉永強, 楊紹普, 廖英英. 一種磁流變阻尼器模型參數識別新方法. 機械工程學報, 2018, 54(6):62 doi: 10.3901/JME.2018.06.062 [21] Ni Y Q, Ko J M, Wong C W. Nonparametric identification of nonlinear hysteretic systems. J Eng Mech, 1999, 125(2): 206 doi: 10.1061/(ASCE)0733-9399(1999)125:2(206) [22] Peng J Y, Li H, Susuki Y. Modeling of nonlinear hysteresis with pinching. J Shenyang Jianzhu Univ Nat Sci, 2005, 21(4): 325彭君義, 李惠, 鈴木祥之. 非線性滑移滯回模型建模. 沈陽建筑大學學報: 自然科學版, 2005, 21(4):325 [23] Liu Y Q, Yang S P, Liao Y Y, et al. Parameter identification of Bouc–wen model for MR damper based on genetic algorithm. J Vib Shock, 2011, 30(7): 261劉永強, 楊紹普, 廖英英, 等. 基于遺傳算法的磁流變阻尼器Bouc–Wen模型參數辨識. 振動與沖擊, 2011, 30(7):261 [24] Liu W D, Liao Y Y, Liu Y Q. Parameter identifying of the rubber damper hysteresis loop based on GA–PS. J Shijiazhuang Tiedao Univ Nat Sci Ed, 2017, 30(4): 46劉偉棟, 廖英英, 劉永強. 基于GA–PS的軌道橡膠隔振器滯回模型參數識別. 石家莊鐵道大學學報: 自然科學版), 2017, 30(4):46 [25] Liao Y Y, Liu Y Q, Liu J X, et al. MRD model parameter identification and its application in vibration control of vehicle. J Vib Meas Diagn, 2012, 32(2): 223廖英英, 劉永強, 劉金喜, 等. MRD模型參數識別及其在振動控制中的應用. 振動、測試與診斷, 2012, 32(2):223 [26] Liu Y Q, Yang S P, Liao Y Y. A quantizing method for determination of controlled damping parameters of magnetorheological damper models. J Intell Mater Syst Struct, 2011, 22(18): 2127 doi: 10.1177/1045389X11425278 -
點擊查看大圖
計量
- 文章訪問數: 3238
- HTML全文瀏覽量: 1061
- PDF下載量: 74
- 被引次數: 0
