Acoustic signal analysis of the resonance frequency region for planetary gearbox fault diagnosis based on high-order synchrosqueezing transform
-
摘要: 建立了非平穩運行工況下行星齒輪箱共振頻帶內的聲音信號解析模型，揭示了齒輪故障特征在聲音信號共振頻帶內的分布規律。根據共振頻率不隨轉速變化的特點定位了齒輪箱共振頻率，為在共振頻帶內提取齒輪故障特征奠定基礎。針對傳統時頻分析方法時頻分辨率低的缺陷，研究了基于高階同步壓縮變換的時變故障特征提取方法。通過數值仿真和實驗信號分析，驗證了所提出的聲音信號模型與行星齒輪箱故障特征分布規律的正確性，以及利用高階同步壓縮變換方法提取共振頻帶內行星齒輪箱故障特征的有效性。Abstract: Planetary gearboxes have one or several planet gears rotating around the sun gear while revolving along their axle. This unique gear structure results in the simultaneous meshing of the planet gear with both sun and ring gears. Because of the high transmission ratio and large bearing capacity of its compact structure, planetary gearboxes have been extensively used in a variety of industrial applications. Therefore, planetary gearbox fault diagnosis is essential to ensure safe and efficient industrial manufacturing. Acoustic signal analysis provides an effective and noninvasive method for detecting potential faults in the planetary gearbox. However, the theoretical foundation of planetary gearbox fault signatures in acoustic signals is ambiguous. In this work, the planetary gearbox acoustic signal model of the resonance frequency region under the nonstationary state is structured by amplitude and frequency modulation, and the gear fault characteristics of the acoustic signals are explicitly derived. Given that resonance frequency is independent of rotational speed, the resonance frequency can be distinguished from speed-related frequency components. This lays the foundation for extracting the gear fault characteristics of the resonance frequency region. Moreover, the planetary gearbox often runs under time-varying speed conditions, and the fault frequency components are time-varying. To overcome the limitations of the traditional time–frequency analysis method in limited time–frequency resolution or cross-term interferences, the appropriate time–frequency analysis method is essential. In this work, the high-order synchrosqueezing transform is exploited to identify the time-varying fault characteristics of the planetary gearbox acoustic signal. Owing to the step of squeezing the energy distributed along instantaneous frequency in frequency direction, time–frequency representation by synchrosqueezing transform achieves a high time–frequency resolution. The high-order interpretation of instantaneous frequency further improves the capability to capture the time–frequency details. The acoustic signal model and corresponding fault characteristics of the planetary gearbox in the resonance frequency region are verified by both numerical simulations and laboratory experiments. The gear defect within the planetary gearbox is successfully diagnosed via the high-order synchrosqueezing transform.
-
Key words:
- resonance /
- synchrosqueezing transform /
- nonstationary /
- planetary gearbox /
- fault diagnosis
-
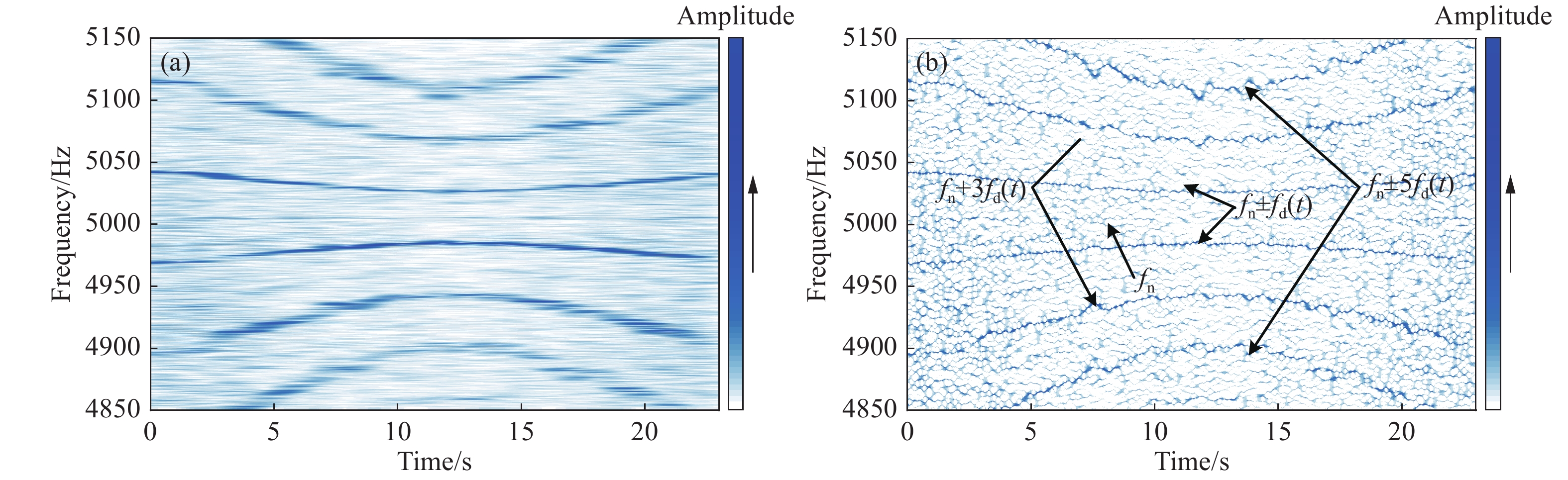
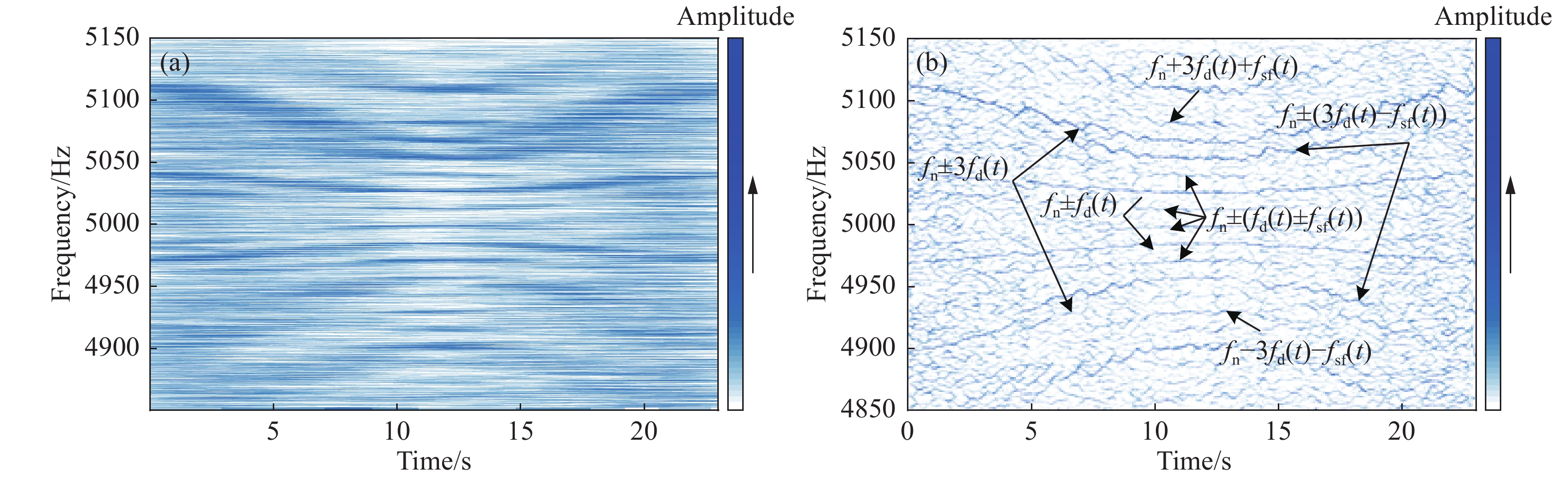
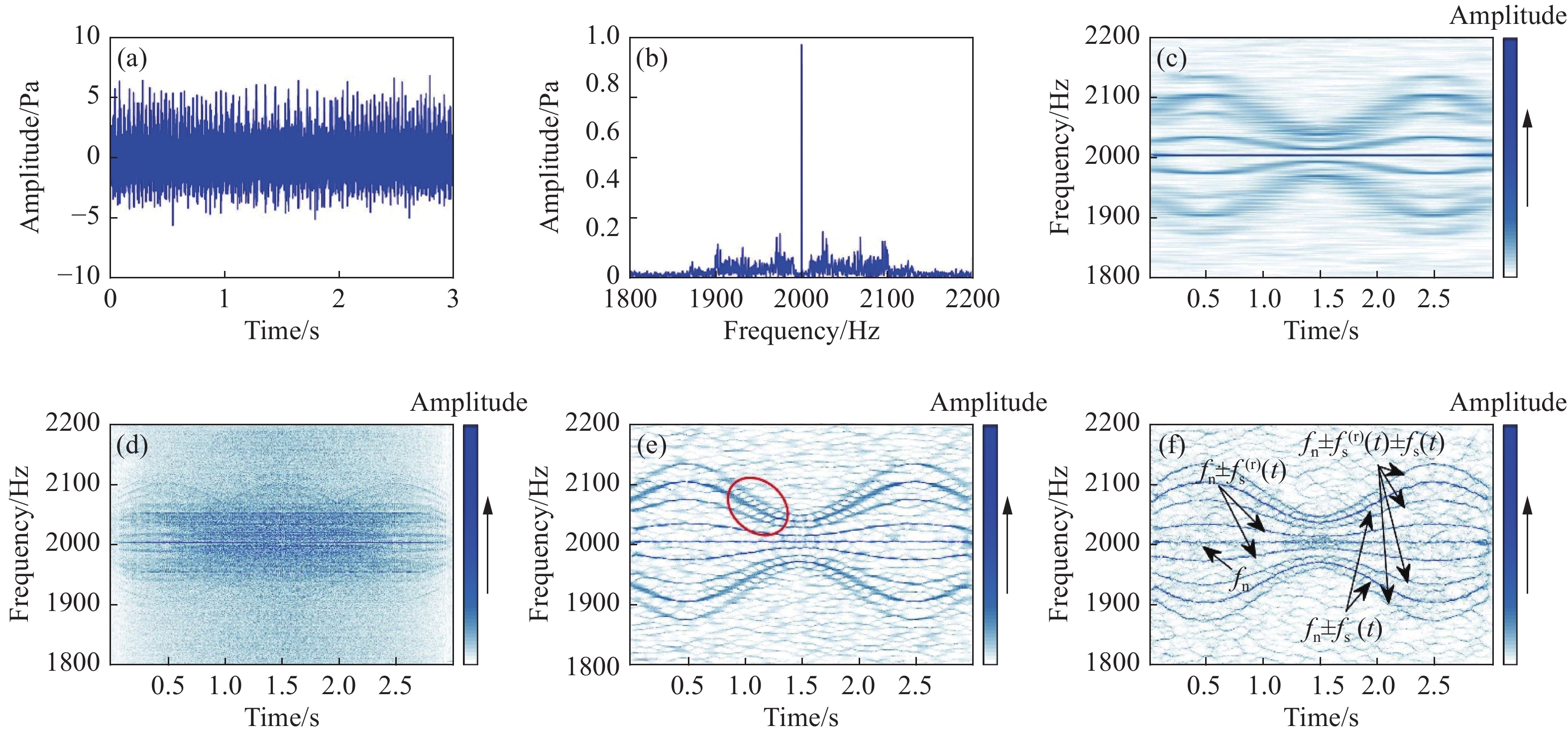
圖 1 仿真信號。（a）波形；（b）Fourier頻譜；（c）STFT時頻分布；（d）Wigner?Ville分布；（e）FSST；（f）FSST4
Figure 1. Simulation signal: (a) waveform; (b) Fourier spectrum; (c) time–frequency representation(TFR) by STFT; (d) Wigner–Ville distribution; (e) time-frequency representation by FSST; (f) time-frequency representation by FSST4
圖 2 實驗裝置。1—電動機；2—定軸齒輪箱；3,5—行星齒輪箱；4—聲壓傳感器；6—磁粉制動器；7—太陽輪故障
Figure 2. Test rig: 1—motor; 2—fixed-shaft gearbox; 3, 5—planetary gearbox; 4—microphone; 6—magnetic powder brake; 7—sun gear fault
圖 3 正常狀態聲音信號分析。（a）STFT時頻分布；（b）FSST4時頻分布
Figure 3. Acoustic signal analysis under normal conditions: (a) TFR by STFT; (d) TFR by FSST4
圖 4 太陽輪故障狀態聲音信號分析；（a）STFT時頻分布；（b）FSST4時頻分布
Figure 4. Acoustic signal analysis under sun gear fault conditions: (a) TFR by STFT; (b) TFR by FSST4
表 1 齒輪箱主要參數
Table 1. Main parameters of gearboxes
Gear Gear teeth number Gear Gear teeth number Gear fault frequency First stage Second stage Input 32 — Sun 20 ${f_{\rm{s}}}{\rm{(}}t{\rm{) = }}(20/27){f_{\rm{d}}}{\rm{(}}t{\rm{)}}$ Intermediate 96 16 Planet 40 (4) ${f_{\rm{p}}}{\rm{(}}t{\rm{) = }}(5/54){f_{\rm{d}}}{\rm{(}}t{\rm{)}}$ Output — 48 Ring 100 ${f_{\rm{r}}}{\rm{(}}t{\rm{) = }}(4/27){f_{\rm{d}}}{\rm{(}}t{\rm{)}}$ Note: the number in the parentheses indicates the number of planet gears. 
下載: 導出CSV
www.77susu.com<span id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> <span id="fpn9h"><noframes id="fpn9h"> <th id="fpn9h"></th> <strike id="fpn9h"><noframes id="fpn9h"><strike id="fpn9h"></strike> <th id="fpn9h"><noframes id="fpn9h"> <span id="fpn9h"><video id="fpn9h"></video></span> <ruby id="fpn9h"></ruby> <strike id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> -
參考文獻
[1] Zhang J Y, Wu S G, Huang S J, et al. Synthetic stiffness degradation behavior of planetary gear set with crack on single tooth. <italic>J Beijing Univ Technol</italic>, 2018, 44(2): 170張建宇, 吳帥剛, 黃勝軍, 等. 單齒裂紋行星輪系合成剛度的劣化特性. 北京工業大學學報, 2018, 44(2):170 [2] Zhang D, Feng Z P. Application of iterative generalized short-time Fourier transform to fault diagnosis of planetary gearboxes. <italic>Chin J Eng</italic>, 2017, 39(4): 604張東, 馮志鵬. 迭代廣義短時Fourier變換在行星齒輪箱故障診斷中的應用. 工程科學學報, 2017, 39(4):604 [3] Zhao C, Feng Z P. Localized fault identification of planetary gearboxes based on multiple-domain manifold. <italic>Chin J Eng</italic>, 2017, 39(5): 769趙川, 馮志鵬. 基于多域流形的行星齒輪箱局部故障識別. 工程科學學報, 2017, 39(5):769 [4] Chen X W, Feng Z P, Liang M. Planetary gearbox fault diagnosis under time-variant conditions based on iterative generalized synchrosqueezing transform. <italic>J Mech Eng</italic>, 2015, 51(1): 131 doi: 10.3901/JME.2015.01.131陳小旺, 馮志鵬, Liang Ming. 基于迭代廣義同步壓縮變換的時變工況行星齒輪箱故障診斷. 機械工程學報, 2015, 51(1):131 doi: 10.3901/JME.2015.01.131 [5] Yang T Q, Tang L W, Zheng H Q, et al. Research on diagnosing gear fault of gearbox by acoustic method. <italic>J Ordnance Eng College</italic>, 2000, 12(4): 24楊通強, 唐力偉, 鄭海起, 等. 基于聲測法的齒輪箱齒輪故障診斷研究. 軍械工程學院學報, 2000, 12(4):24 [6] Lin J. Feature extraction of machine sound using wavelet and its application in fault diagnosis. <italic>NDT </italic>&<italic>E Int</italic>, 2001, 34(1): 25 [7] Rezaei A, Dadouche A, Wickramasinghe V, et al. A comparison study between acoustic sensors for bearing fault detection under different speed and load using a variety of signal processing techniques. <italic>Tribol Trans</italic>, 2011, 54(2): 179 doi: 10.1080/10402004.2010.533817 [8] Metwalley S M, Hammad N, Abouel-Seoud S A. Vehicle gearbox fault diagnosis using noise measurements. <italic>Int J Energy Environ</italic>, 2011, 2(2): 357 [9] Baydar N, Ball A. A comparative study of acoustic and vibration signals in detection of gear failures using Wigner–Ville distribution. <italic>Mech Syst Signal Process</italic>, 2001, 15(6): 1091 doi: 10.1006/mssp.2000.1338 [10] Feng Z P, Chen X W, Liang M, et al. Time-frequency demodulation analysis based on iterative generalized demodulation for fault diagnosis of planetary gearbox under nonstationary conditions. <italic>Mech Syst Signal Process</italic>, 2015, 62-63: 54 doi: 10.1016/j.ymssp.2015.03.014 [11] Chen X W, Feng Z P. Application of reassigned wavelet scalogram in wind turbine planetary gearbox fault diagnosis under nonstationary conditions. <italic>Shock Vib</italic>, 2016: 6723267 [12] Chen X W, Feng Z P. Time-frequency analysis of torsional vibration signals in resonance region for planetary gearbox fault diagnosis under variable speed conditions. <italic>IEEE Access</italic>, 2017, 5: 21918 doi: 10.1109/ACCESS.2017.2763172 [13] Wang W Y. Early detection of gear tooth cracking using the resonance demodulation technique. <italic>Mech Syst Signal Process</italic>, 2001, 15(5): 887 doi: 10.1006/mssp.2001.1416 [14] Feng Z P, Liang M, Chu F L. Recent advances in time-frequency analysis methods for machinery fault diagnosis: a review with application examples. <italic>Mech Syst Signal Process</italic>, 2013, 38(1): 165 doi: 10.1016/j.ymssp.2013.01.017 [15] Hlawatsch F, Auger F. Time-Frequency Analysis: Concepts and Methods. Hoboken: John Wiley & Sons, 2008 [16] Feng Z P, Chen X W Liang M. Iterative generalized synchrosqueezing transform for fault diagnosis of wind turbine planetary gearbox under nonstationary conditions. <italic>Mech Syst Signal Process</italic>, 2015, 52-53: 360 doi: 10.1016/j.ymssp.2014.07.009 [17] Martin W, Flandrin P. Wigner–Ville spectral analysis of nonstationary processes. <italic>IEEE Trans Acoust Speech Signal Process</italic>, 1985, 33(6): 1461 doi: 10.1109/TASSP.1985.1164760 [18] Auger F, Flandrin P. Improving the readability of time-frequency and time-scale representations by the reassignment method. <italic>IEEE Trans Signal Process</italic>, 1995, 43(5): 1068 doi: 10.1109/78.382394 [19] Daubechies I, Lu J F, Wu H T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. <italic>Appl Comput Harmon Anal</italic>, 2011, 30(2): 243 doi: 10.1016/j.acha.2010.08.002 [20] Yang H Z. Statistical analysis of synchrosqueezed transforms. <italic>Appl Comput Harmon Anal</italic>, 2018, 45(3): 526 doi: 10.1016/j.acha.2017.01.001 [21] Thakur G, Brevdo E, Fuckar N S, et al. The Synchrosqueezing algorithm for time-varying spectral analysis: robustness properties and new paleoclimate applications. <italic>Signal Process</italic>, 2013, 93(5): 1079 doi: 10.1016/j.sigpro.2012.11.029 [22] Yang H Z. Robustness analysis of synchrosqueezed transforms. <italic>Statistics</italic>, 2014: 1 [23] Latsenko D, McClintock P V E, Stefanovska A. Extraction of instantaneous frequencies from ridges in time–frequency representations of signals. <italic>Signal Process</italic>, 2016, 125: 290 doi: 10.1016/j.sigpro.2016.01.024 [24] Pham D H, Meignen S. High-order synchrosqueezing transform for multicomponent signals analysis—with an application to gravitational-wave signal. <italic>IEEE Trans Signal Process</italic>, 2017, 65(12): 3168 doi: 10.1109/TSP.2017.2686355 [25] Oberlin T, Meignen S, Perrier V. Second-order synchrosqueezing transform or invertible reassignment? towards ideal time-frequency representations. <italic>IEEE Trans Signal Process</italic>, 2015, 63(5): 1335 doi: 10.1109/TSP.2015.2391077 -
點擊查看大圖
圖(4) / 表(1)
計量
- 文章訪問數: 1714
- HTML全文瀏覽量: 1107
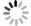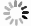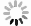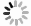
- PDF下載量: 69
- 被引次數: 0
