Optimization research of planetary roller screw mechanism parameters based on crow search algorithm
-
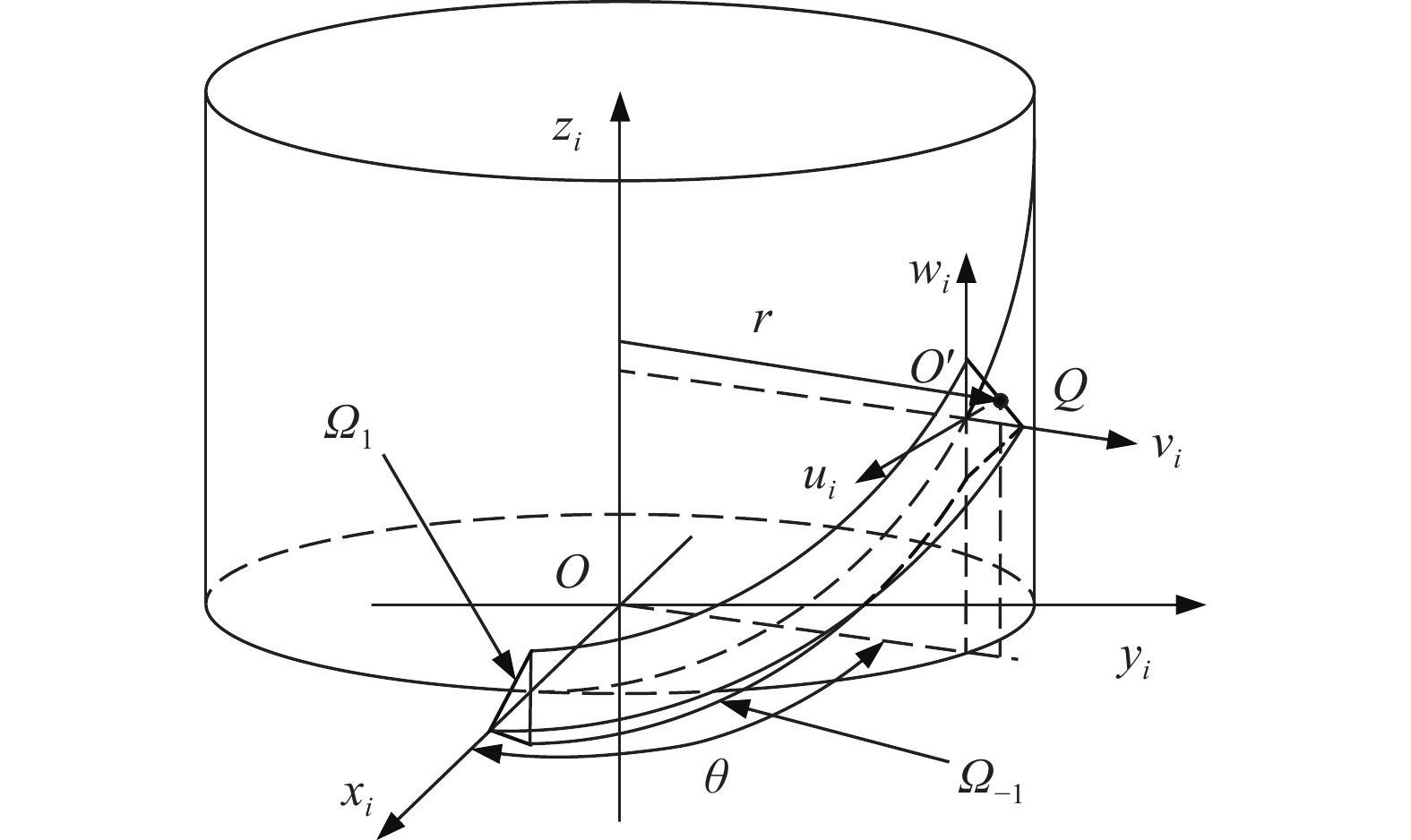
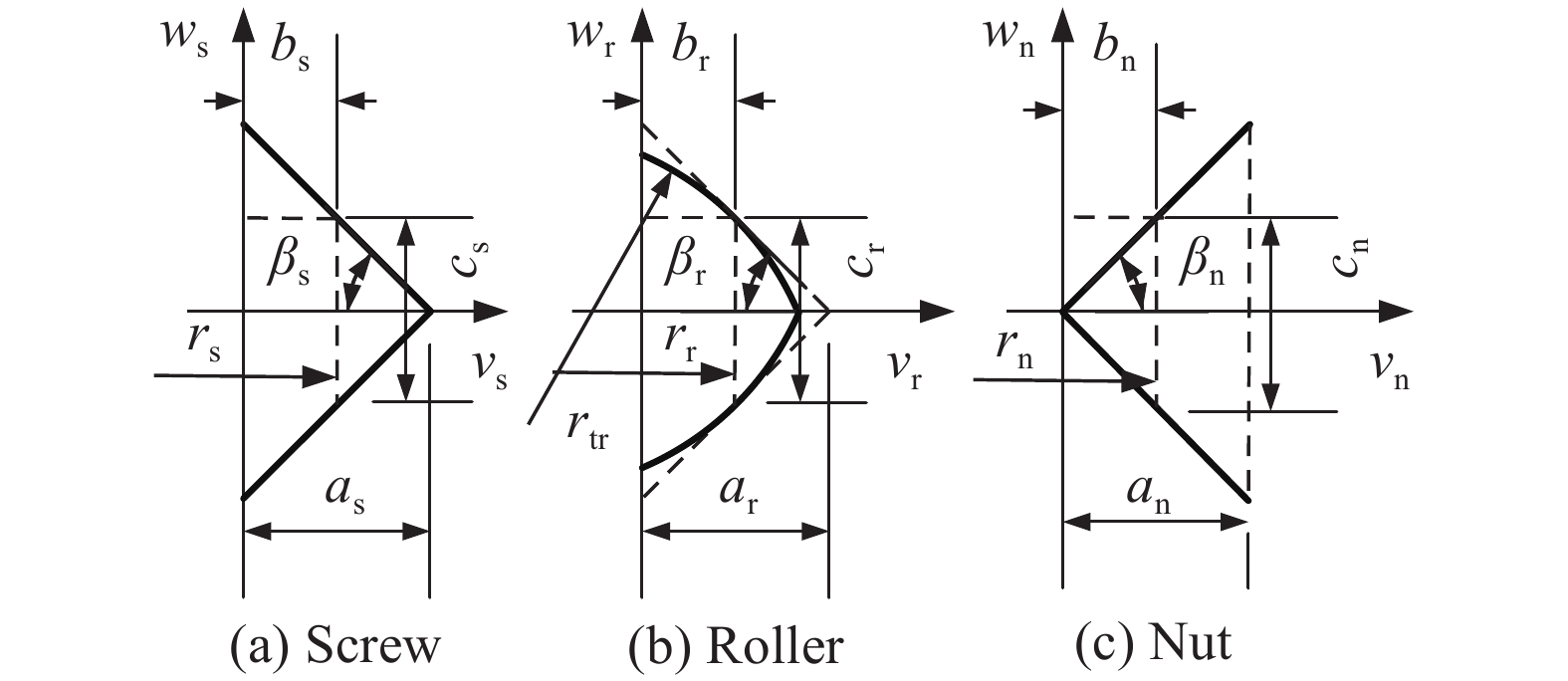
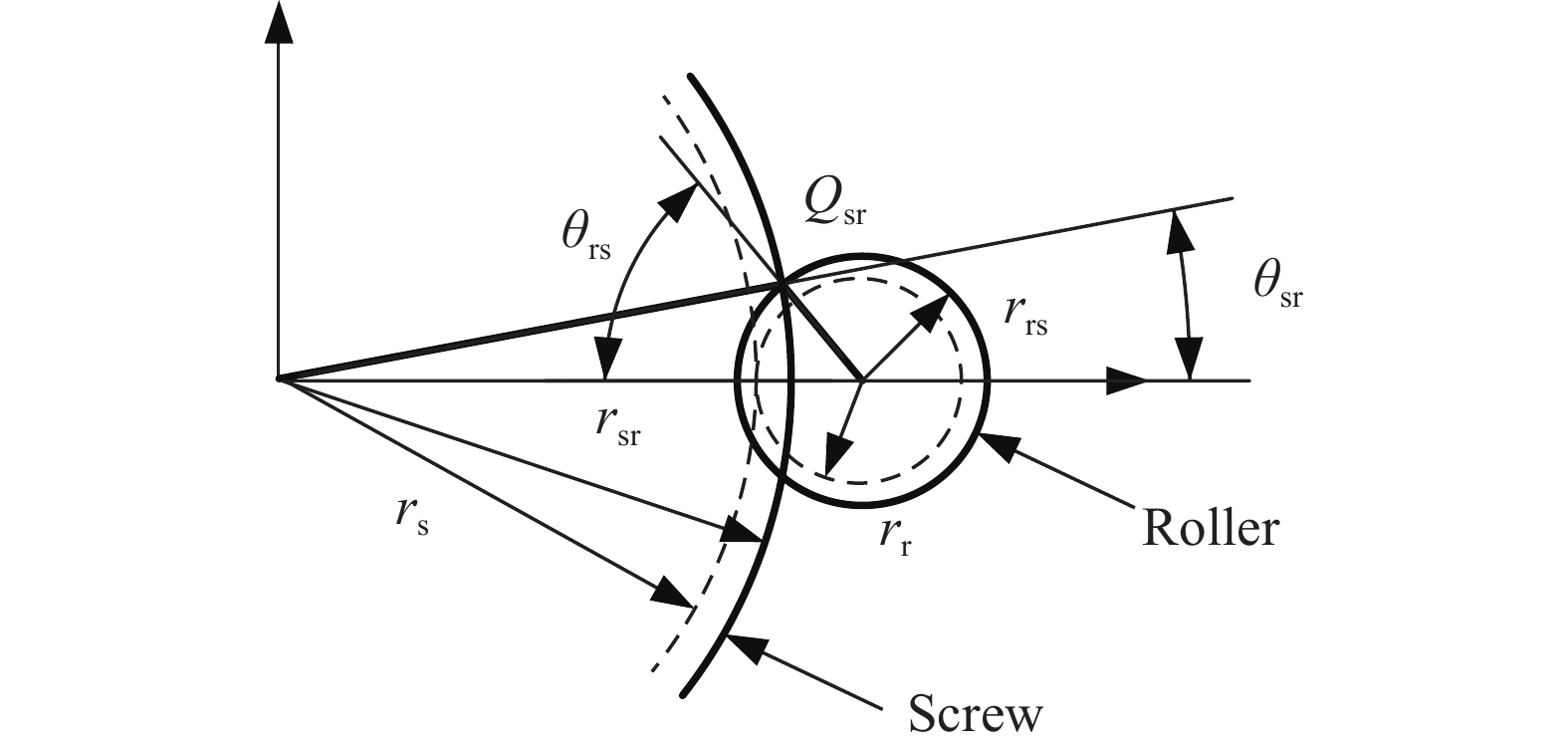
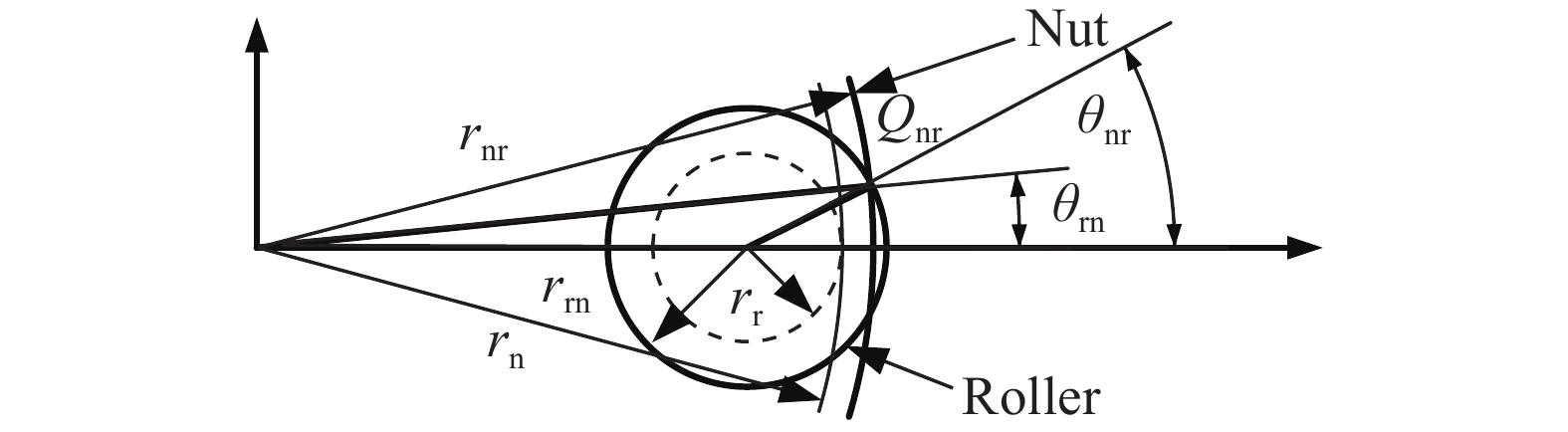
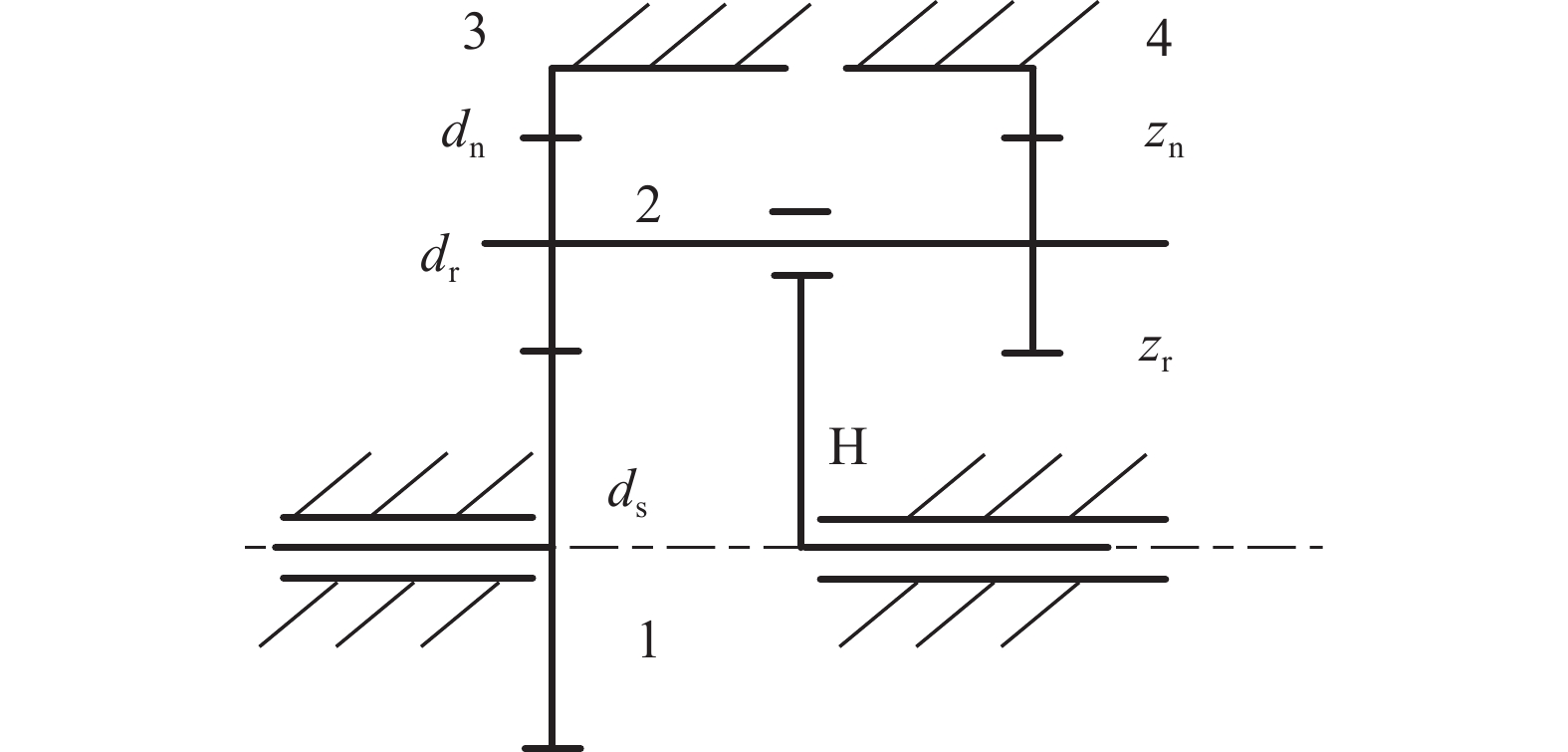
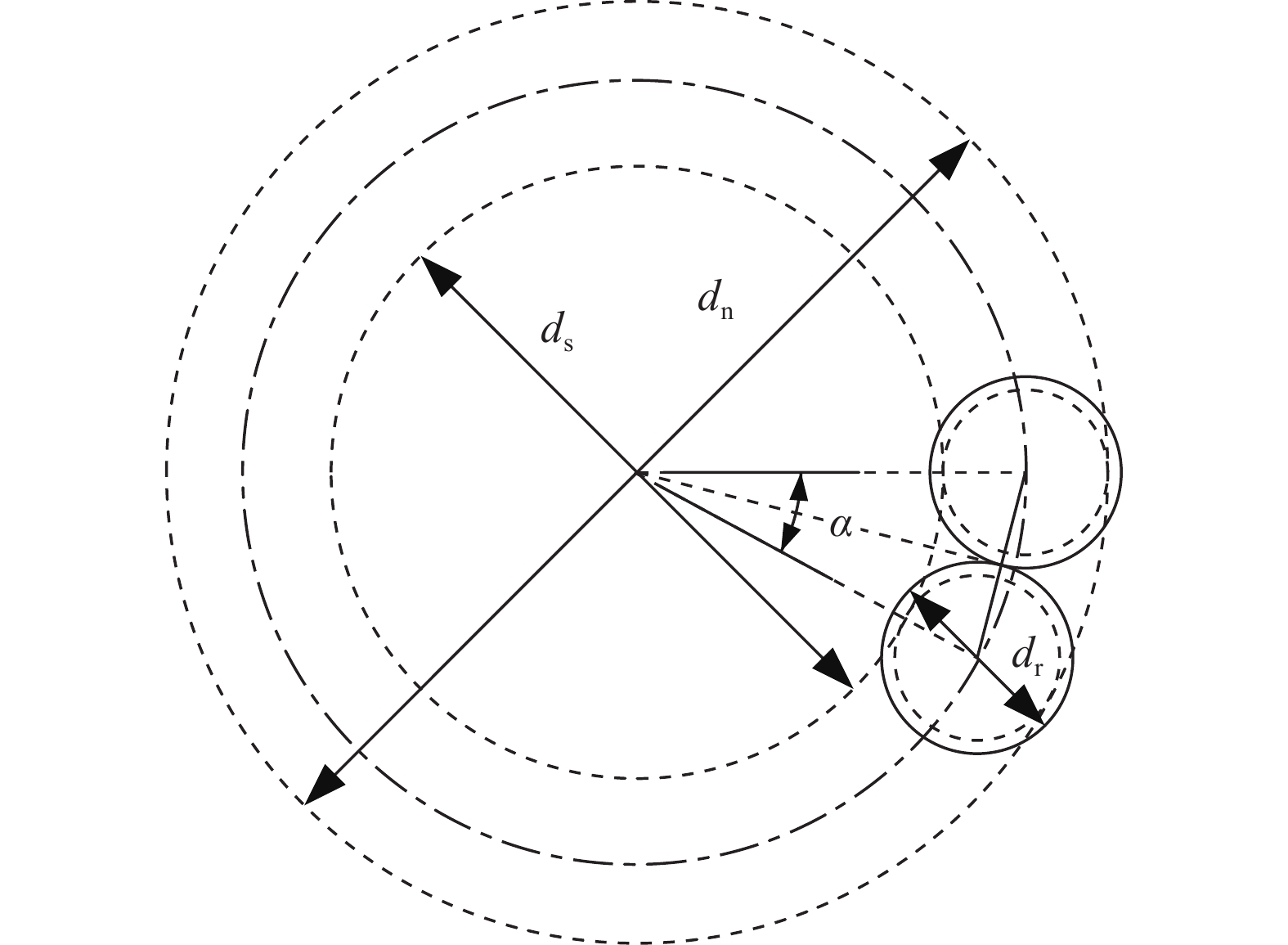
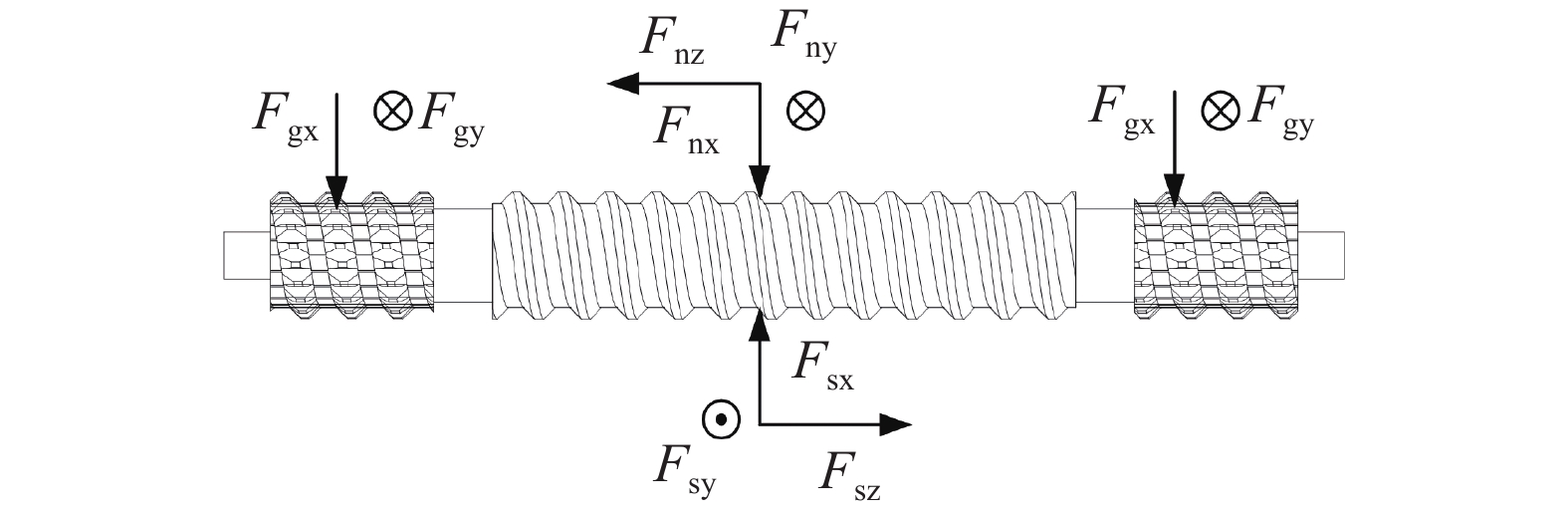
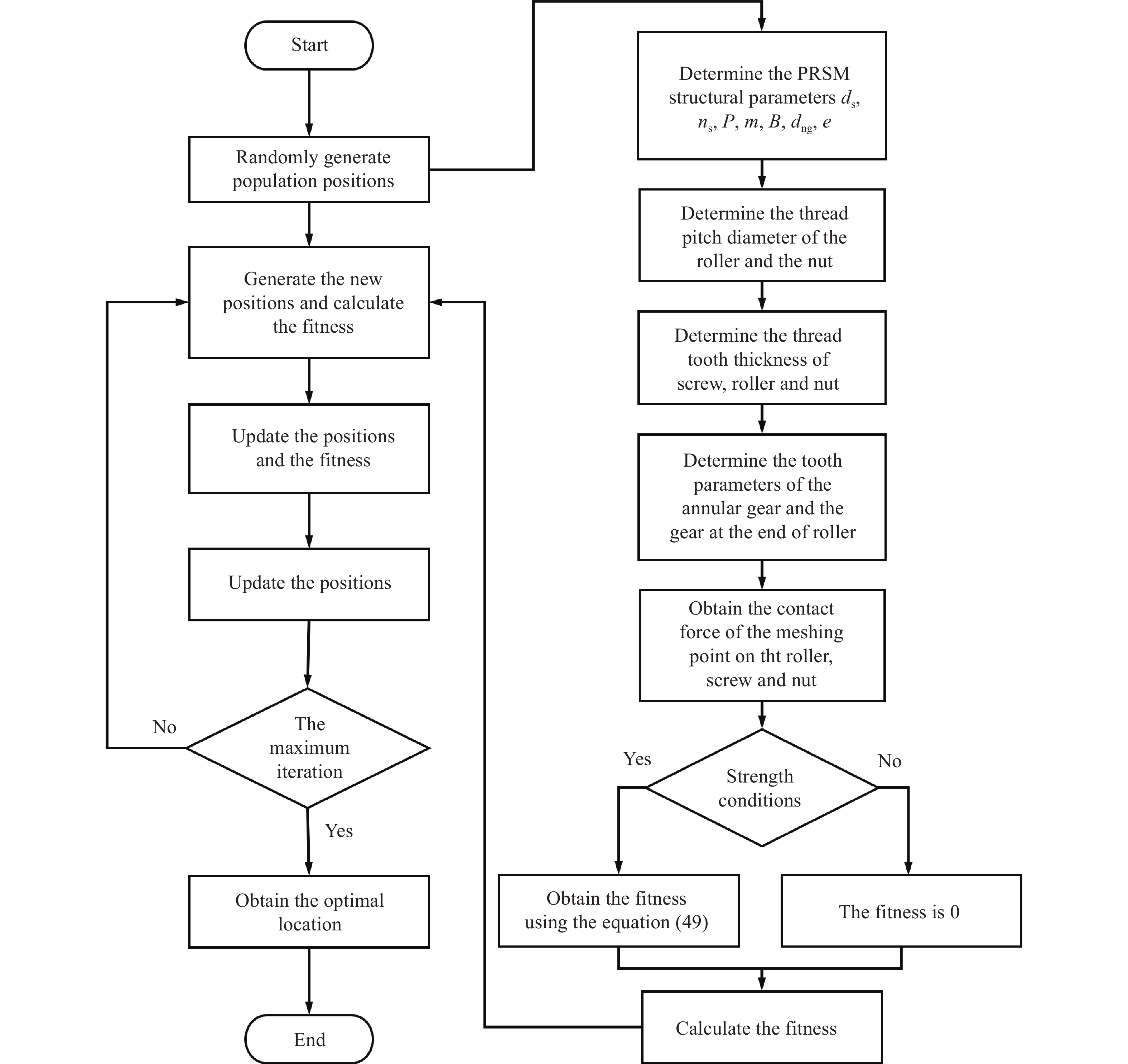
摘要: 針對行星滾柱絲杠結構參數匹配問題,提出一種基于烏鴉搜索算法的參數優化模型。考慮行星滾柱絲杠螺紋嚙合點位置的影響,建立絲杠、滾柱以及螺母空間螺旋曲面方程,得到螺紋嚙合點處位置與螺紋牙厚之間的關系。根據螺紋副和齒輪副嚙合關系,確定內齒圈和滾柱端部輪齒設計參數。利用空間螺旋曲面方程,獲得螺紋嚙合點處的法向量,并推導行星滾柱絲杠各零件間的受力關系。以行星滾柱絲杠結構參數作為設計變量,以螺母外徑、絲杠中徑、滾柱長度等參數最小為優化目標,考慮行星滾柱絲杠結構約束和主要承力部件強度約束,利用烏鴉搜索算法作為優化算法,建立行星滾柱絲杠參數優化模型,從而實現優化變量最佳匹配。最后,針對三種負載,利用該優化模型得到三組行星滾柱絲杠結構參數,并將其優化結果與國外產品手冊進行對比,從而驗證了本文優化模型有效性。Abstract: Because structural parameter matching has a strong influence on the service behavior of planetary roller screw mechanisms (PRSM), understanding how to effectively design the structural parameters of PRSM is highly important in practical industrial applications. This study proposes a parameter optimization model based on a crow search algorithm (CSA) to solve the structural parameter matching problem of PRSM. The relationship between the main structural parameters of PRSM can be deduced according to the working principle and geometric conditions. The screw, roller, and nut space spiral surface equation are established by considering the influence of the meshing point position of PRSM on thread meshing clearance. The relationship between the meshing point position and PRSM tooth thickness is obtained using the tangent contact condition of the spiral surface. To achieve no backlash meshing and improve PRSM transmission accuracy, the thread tooth thickness of the screw, roller, and nut can be adjusted. According to the meshing relationship between the thread pair and the gear pair of PRSM, the structural parameters of the annular gear and the gear at the end of the roller are determined. The normal vectors at the meshing point of the screw, roller, and nut are calculated using space spiral surface equations. To test the strength of the PRSM, static analysis of the roller is used to deduce the force relations between the main parts of the PRSM. PRSM structural parameters serve as design variables. An optimization goal is to reduce the outer diameter of the nut, the nominal diameter of the screw, and the length of the roller. The spatial structure constraints and component strength constraints of PRSM are considered. The CSA was introduced to be the optimization algorithm. The parameter optimization model of PRSM is established for achieving optimum matching of the optimization variables. Finally, using the proposed optimization model, three groups of PRSM structural parameters are obtained for three different types of load. In this study, the optimization results are compared with a foreign PRSM product manual to validate the effectiveness of the optimization model. The results show that the PRSM structural parameters obtained from the proposed model are essentially consistent with those from the foreign PRSM product manual. Furthermore, the proposed model provides the structural parameters of thread teeth, which are not included in the foreign product manual. The proposed PRSM optimization model is promising for its application in actual production.
-
Material properties Corresponding value/MPa Ultimate tensile strength 2073 Ultimate shear strength 1036.5 Ultimate bending strength 3200 Bending fatigue limit 735 Contact fatigue limit 1400 表 2 PRSM結構參數對比
Table 2. Comparison of PRSM structure parameters
Structure parameter F = 51000 N F = 102100 N F = 221600 N Proposed model Rollvis Proposed model Rollvis Proposed model Rollvis Nominal diameter of screw/mm 15 15 20 19.5 29 30 Nominal diameter of roller/mm 5 5 6.67 6.5 9.67 10 Pitch diameter of nut/mm 25 25 33.33 32.5 48.33 50 Pitch of thread/mm 0.4 0.4 0.6 0.4 1 0.8 Starts of screw thread 5 5 5 5 5 5 External diameter of nut/mm 31.4180 26 39.20 42 56.41 62 Thread tooth thickness of roller/mm 0.216 — 0.304 — 0.484 — Thread tooth thickness of screw/mm 0.1754 — 0.2814 — 0.488 — Thread tooth thickness of nut/mm 0.184 — 0.296 — 0.516 — Teeth number of annular gear 20 — 26 — 38 — Teeth number of gear at the end of the roller 100 — 130 — 190 — Modulus/mm 0.25 — 0.25 — 0.25 — Modification coefficient of annular gear –0.3680 — 0.1413 — 0.5013 — Modification coefficient of gear at the end of the roller 0.3680 — –0.1413 — –0.5013 — www.77susu.com<span id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> <span id="fpn9h"><noframes id="fpn9h"> <th id="fpn9h"></th> <strike id="fpn9h"><noframes id="fpn9h"><strike id="fpn9h"></strike> <th id="fpn9h"><noframes id="fpn9h"> <span id="fpn9h"><video id="fpn9h"></video></span> <ruby id="fpn9h"></ruby> <strike id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> -
參考文獻
[1] Yao Q, Zhang M C, Liu Y S, et al. Multi-objective optimization of planetary roller screw mechanism based on improved mathematical modelling. Tribol Int, 2021, 161: 107095 doi: 10.1016/j.triboint.2021.107095 [2] Kim N S, Kim K, Jong S. Contact analysis and static load carrying capacity of planetary roller screw mechanism. https://doi.org/10.21203/rs.3.rs-106438/v1 [3] Meng J J, Du X, Li Y M, et al. A multiscale accuracy degradation prediction method of planetary roller screw mechanism based on fractal theory considering thread surface roughness. Fractal Fract, 2021, 5(4): 237 doi: 10.3390/fractalfract5040237 [4] Du X, Chen B K, Zheng Z D. Investigation on mechanical behavior of planetary roller screw mechanism with the effects of external loads and machining errors. Tribol Int, 2021, 154: 106689 doi: 10.1016/j.triboint.2020.106689 [5] Du C M, Liu G, Qiao G, et al. Transient thermal analysis of standard planetary roller screw mechanism based on finite element method. Adv Mech Eng, 2018, 10(12): 168781401881230 [6] Li L J, Fu Y L, Zheng S C, et al. Friction torque analysis of planetary roller screw mechanism in roller jamming. Math Probl Eng, 2020, 2020(12): 1 [7] Garcia A, Cusido I, Rosero J A, et al. Reliable electro-mechanical actuators in aircraft. IEEE Aerosp Electron Syst Mag, 2008, 23(8): 19 doi: 10.1109/MAES.2008.4607895 [8] Zhou M. Disturbance Analysis and Control of Electromechanical Actuator System [Dissertation]. Changchun: Institute of Physics, Chinese Academy of Sciences, 2020周滿. 電動舵機系統擾動分析與控制策略研究[學位論文]. 長春: 中國科學院大學(中國科學院長春光學精密機械與物理研究所), 2020 [9] Zheng W, Zu L, Wang K. Experiment research on influence factors of travel error of planetary roller screw pair. Chin J Sci Instrum, 2021, 42(9): 214 doi: 10.19650/j.cnki.cjsi.J2108059鄭偉, 祖莉, 王凱. 精密行星滾柱絲杠副行程誤差影響因素試驗研究. 儀器儀表學報, 2021, 42(9):214 doi: 10.19650/j.cnki.cjsi.J2108059 [10] Ma S J, Liu G, Tong R T, et al. A frictional heat model of planetary roller screw mechanism considering load distribution. Mech Based Des Struct Mach, 2015, 43(2): 164 doi: 10.1080/15397734.2014.938816 [11] Zhao Y, Ni J, Lu L N. Mesh calculation of roller screw pair. Mach Des, 2003, 20(3): 34 doi: 10.3969/j.issn.1001-2354.2003.03.012趙英, 倪潔, 呂麗娜. 滾柱絲杠副的嚙合計算. 機械設計, 2003, 20(3):34 doi: 10.3969/j.issn.1001-2354.2003.03.012 [12] Cheng Y, Fan Y X. Analysis of effect of thread error for meshing state of planetary roller screw. Modul Mach Tool &Autom Manuf Tech, 2018(4): 119 doi: 10.13462/j.cnki.mmtamt.2018.04.029程遠, 范元勛. 行星滾柱絲杠螺紋誤差對嚙合狀態影響分析. 組合機床與自動化加工技術, 2018(4):119 doi: 10.13462/j.cnki.mmtamt.2018.04.029 [13] Fu X J, Liu G, Ma S J, et al. Studies on meshing mechanism of helical surfaces in planetary roller screw mechanism. J Mech Eng, 2016, 52(3): 26 doi: 10.3901/JME.2016.03.026付曉軍, 劉更, 馬尚君, 等. 行星滾柱絲杠副螺旋曲面嚙合機理研究. 機械工程學報, 2016, 52(3):26 doi: 10.3901/JME.2016.03.026 [14] Ryakhovskiy O A, Sorokin F D, Marokhin A S. Calculation of radial displacements of nut and rollers axes and the position of a contact between the nut and the roller thread in an inverted planetary roller screw mechanism. Higher Educational Institutions Machine Building, 2013, 11: 12 [15] Sandu S, Biboulet N, Nelias D, et al. An efficient method for analyzing the roller screw thread geometry. Mech Mach Theory, 2018, 126: 243 doi: 10.1016/j.mechmachtheory.2018.04.004 [16] Velinsky S A, Chu B, Lasky T A. Kinematics and efficiency analysis of the planetary roller screw mechanism. J Mech Des, 2009, 131(1): 011016 doi: 10.1115/1.3042158 [17] Dang J L, Liu G, Ma S J, et al. Motion principle and simulation analysis of inverted planetary roller screw mechanism. J Syst Simul, 2013, 25(7): 1646 doi: 10.16182/j.cnki.joss.2013.07.005黨金良, 劉更, 馬尚君, 等. 反向式行星滾柱絲杠機構運動原理及仿真分析. 系統仿真學報, 2013, 25(7):1646 doi: 10.16182/j.cnki.joss.2013.07.005 [18] Xing S, Hou H L, Zhao Y Q, et al. Parametric design and research of planetary roller screw mechanism. J Shaanxi Univ Technol (Nat Sci Ed), 2017, 33(3): 10邢思, 侯紅玲, 趙永強, 等. 行星滾柱絲杠副的參數化設計與研究. 陜西理工大學學報(自然科學版), 2017, 33(3):10 [19] Wei Z X, Yang J J, Zhu J S, et al. Optimized analysis on structural parameter for planetary roller screw. J Mech Transm, 2011, 35(6): 44 doi: 10.3969/j.issn.1004-2539.2011.06.012韋振興, 楊家軍, 朱繼生, 等. 行星滾柱絲杠副的結構參數優化分析. 機械傳動, 2011, 35(6):44 doi: 10.3969/j.issn.1004-2539.2011.06.012 [20] Gao Y, Yang J J, Liang H, et al. Optimization of planetary roller screw gear modification coefficient. J Hubei Univ Technol, 2015, 30(4): 58 doi: 10.3969/j.issn.1003-4684.2015.04.015高揚, 楊家軍, 梁漢, 等. 行星滾柱絲杠副齒輪變位系數的優化. 湖北工業大學學報, 2015, 30(4):58 doi: 10.3969/j.issn.1003-4684.2015.04.015 [21] Wang J L. The Transmission Characteristics Research on Planetary Roller Screw Pair [Dissertation]. Wuhan: Huazhong University of Science and Technology, 2017汪佳麗. 行星滾柱絲杠副傳動特性的研究[學位論文]. 武漢: 華中科技大學, 2017 [22] Askarzadeh A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm. Comput Struct, 2016, 169: 1 doi: 10.1016/j.compstruc.2016.03.001 [23] Zhang W J. Calculation Model and Methods of Load Distribution Over Threads in the Planetary Roller Screw Mechanism [Dissertation]. Xi'an: Northwestern Polytechnical University, 2017張文杰. 行星滾柱絲杠副螺紋牙載荷分布計算模型與方法[學位論文]. 西安: 西北工業大學, 2017 [24] Committee of China Aeronautical Materials Handbook. China Aeronautical Materials Handbook. 2nd Ed. Beijing: Standards Press of China, 2001中國航空材料編輯委員會. 中國航空材料手冊. 2版. 北京: 中國標準出版社, 2001 [25] Rollvis Swiss. Satellite Roller Screws. Genève: Rollvis SA, 2019 -




 下載:
下載: