單軸壓縮條件下裂隙粗糙度對滲透系數的影響

王帥; 于慶磊; 王玲

doi:10.13374/j.issn2095-9389.2020.05.26.001

單軸壓縮條件下裂隙粗糙度對滲透系數的影響

doi: 10.13374/j.issn2095-9389.2020.05.26.001

王帥^1, ,,
于慶磊²,
王玲¹

1.
華北理工大學礦業工程學院，唐山 063210
2.
東北大學巖石破裂與失穩研究中心，沈陽 110004

基金項目: 國家自然科學基金資助項目（51574060）；國家重點研發計劃資助項目（2016YFC0801602）；唐山市科技計劃資助項目（19130216g）

詳細信息

通訊作者:
E-mail：wangshuai@ncst.edu.cn

中圖分類號: TG142.71
計量
- 文章訪問數: 1946
- HTML全文瀏覽量: 720
- PDF下載量: 105
- 被引次數: 0
出版歷程
- 收稿日期: 2020-05-26
- 網絡出版日期: 2020-07-17
- 刊出日期: 2021-07-01

Effect of fracture roughness on permeability coefficient under uniaxial compression

1.
School of Mining Engineering, North China University of Science and Technology, Tangshan 063210, China
2.
Center for Rock Instability & Seismicity Research, Northeastern University, Shenyang 110004, China

More Information

Corresponding author: E-mail: wangshuai@ncst.edu.cn

摘要

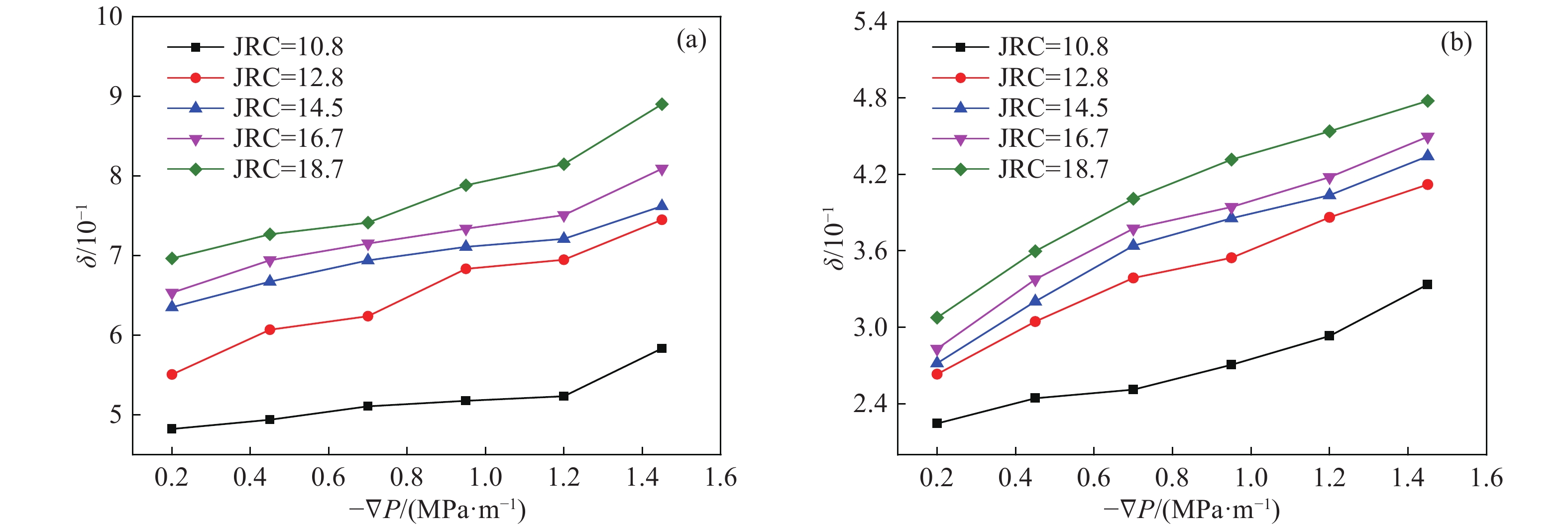
摘要: 裂隙粗糙度是影響裂隙巖體滲流特性和流體流動復雜性的重要因素，為了深入研究單軸壓縮條件下粗糙度對滲透系數的影響，采用3D打印技術和數字建模方法制備了粗糙度不同的裂隙試樣，通過自制的試驗裝置對不同法向壓力下的裂隙試樣進行了試驗。結果表明，在沒有法向壓力的條件下，隨著粗糙度的增加，滲透系數以負指數函數形式減小，采用Forchheimer方程定量的分析了滲流流量與水力梯度之間的非線性關系，Forchheimer方程可以很好地描述粗糙裂隙表面的流動過程，線性項系數隨著粗糙度的增大而減小，非線性項系數隨著粗糙度的增大而增大；在恒定法向壓力且大于水壓的條件下，裂隙試樣的滲透系數隨著粗糙度的增大線性減小，隨著水壓的增大，粗糙度對滲透系數的影響作用增強；定義了系數$\delta $，分析了在有無法向壓力條件下，粗糙度對滲透系數影響的差異性，$\delta $隨著水力梯度的增加而增加，隨著法向壓力的增加而減小。研究結果可以加深對粗糙裂隙表面流體流動的認識，為進一步研究巖體流動特性奠定堅實的基礎。
- 粗糙度 /
- 滲透系數 /
- 裂隙試樣 /
- 3D打印 /
- 單軸壓縮
Abstract: The surface roughness of natural rock-fractures is an important factor affecting the fractured rock mass flow characteristics and further complicating the flow process in the natural fractures. To further study the influence of the fracture surface roughness on the permeability coefficient under uniaxial compression and different hydraulic pressures, 3D printing technology and digital modeling were utilized to prepare the fracture specimens with different fracture surface roughnesses and laboratory permeability tests were conducted through a self-made testing device under different normal pressures and different hydraulic pressures. The experimental results show that in the absence of normal pressure, the rough fracture specimens permeability decreases in a negative exponential form with the increase in the fracture surface roughness. The Forchheimer equation is used to quantitatively describe the nonlinear relationship between seepage flow rate and hydraulic gradients. The regression analyses of the experimental data indicate that the Forchheimer equation provides a good description of the flow process through the rough fracture surface. With the increase in the fracture surface roughness, the linear term coefficient decreases, while the nonlinear term coefficient increases. Under the conditions of fixed normal pressure and normal pressure greater than hydraulic pressure, the fracture specimens permeability decreases linearly with the increase in the fracture surface roughness, and the influence of the fracture surface roughness on the permeability increases with the increase in the hydraulic pressure. The coefficient $\delta $ was used to analyze the difference between the influences of fracture surface roughness on the permeability under normal pressure and without normal pressure. The coefficient $\delta $ increases with the increase in the hydraulic gradients and decreases with the increase in the normal pressure. The results can further clarify the fluid flow through rough fracture surfaces and provide a solid foundation for further research in the fields of rock mass flow characteristics.
- roughness /
- permeability coefficient /
- fracture sample /
- 3D printing /
- uniaxial compression

HTML全文

圖 1 掃描JRC的標準曲線圖

Figure 1. Standard profile curve of JRC

下載: 全尺寸圖片幻燈片

圖 2 吻合的裂隙曲線圖

Figure 2. Curve diagram of mating fracture

下載: 全尺寸圖片幻燈片

圖 3 粗糙裂隙三維模型示意圖

Figure 3. Rough fracture 3D model diagram

下載: 全尺寸圖片幻燈片

圖 4 Makebot程序中建立的三維模型

Figure 4. 3D model established in Makebot

下載: 全尺寸圖片幻燈片

圖 5 打印成型的三維實體模型

Figure 5. 3D solid model of printing molding

下載: 全尺寸圖片幻燈片

圖 6 RayBot 3D打印機

Figure 6. RayBot 3D printer

下載: 全尺寸圖片幻燈片

圖 7 試驗系統裝置示意圖

Figure 7. Schematic of the test system device

下載: 全尺寸圖片幻燈片

圖 8 法向加載系統

Figure 8. Normal loading system

下載: 全尺寸圖片幻燈片

圖 9 模擬裂隙系統

Figure 9. Simulated fracture system

下載: 全尺寸圖片幻燈片

圖 10 不同水壓下JRC與K₀的關系曲線

Figure 10. Relationship between JRC and K₀ under different hydraulics pressures

下載: 全尺寸圖片幻燈片

圖 11 流體在粗糙裂隙中流動示意圖

Figure 11. Schematic of fluid flow in rough fracture

下載: 全尺寸圖片幻燈片

圖 12 不同粗糙度裂隙$ - \nabla P$與Q的關系曲線

Figure 12. Relationship between $ - \nabla P$ and Q with different roughness fractures

下載: 全尺寸圖片幻燈片

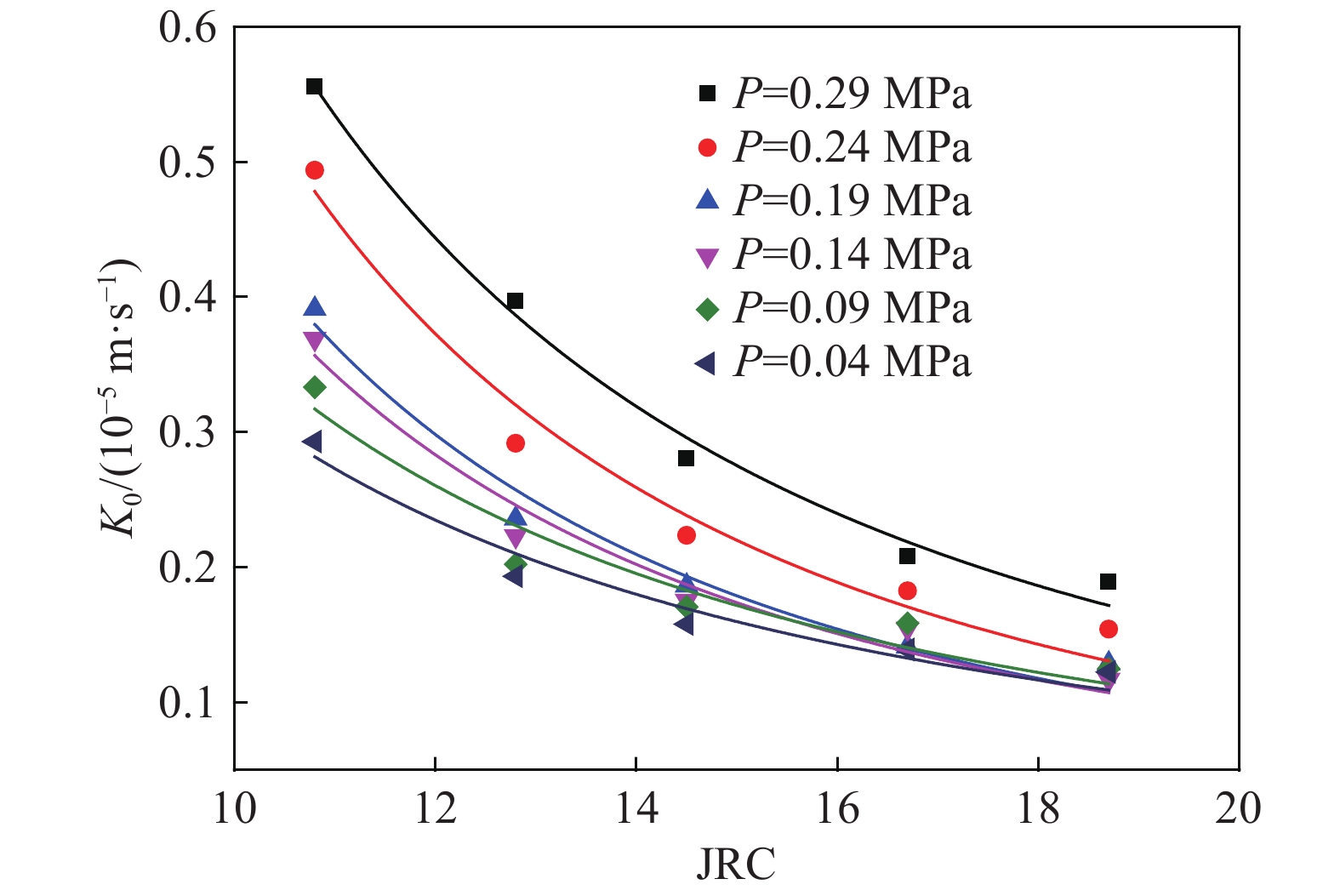
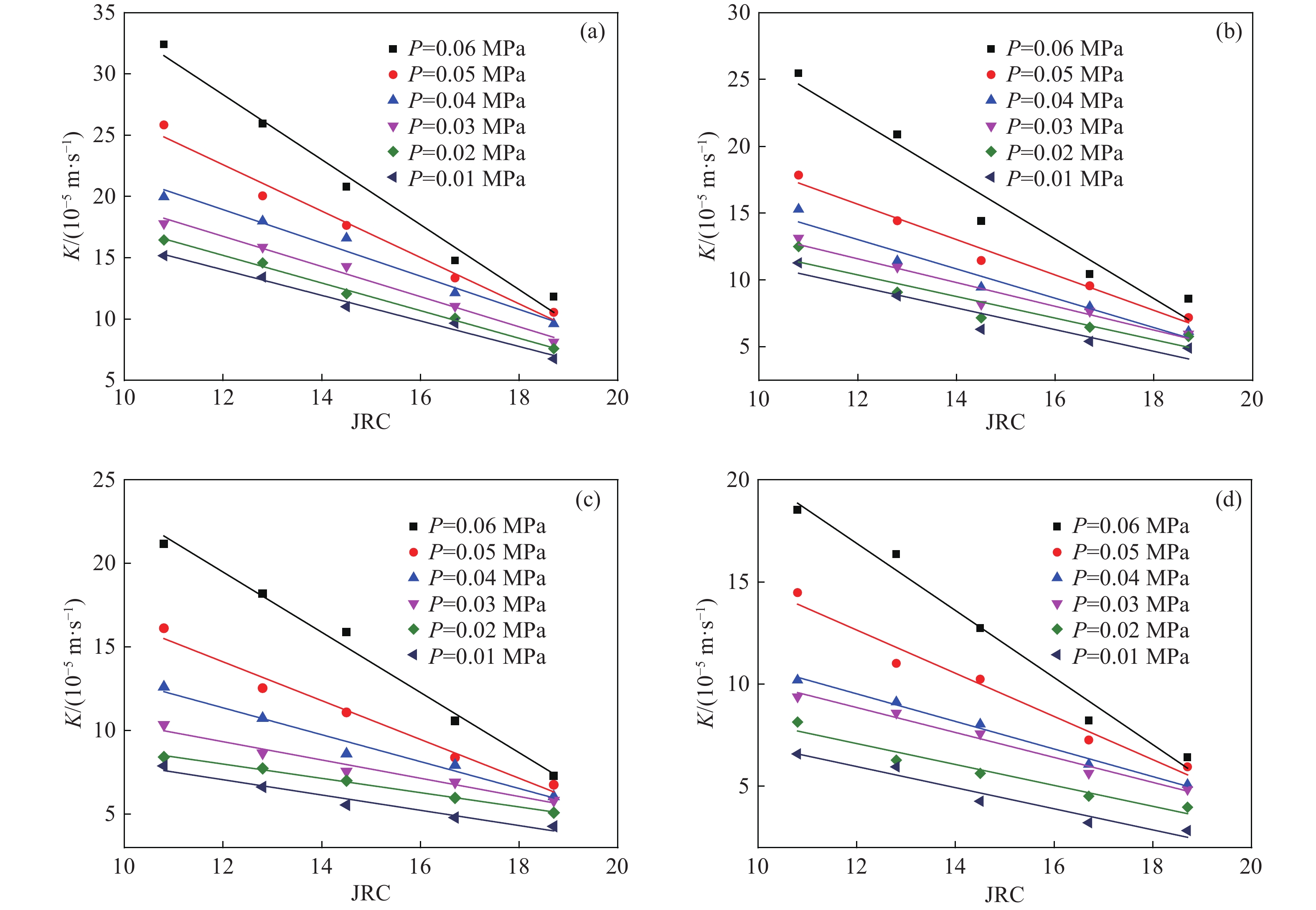
圖 13 法向壓力恒定不同水壓下JRC與K的關系曲線。（a）法向壓力為0.25 MPa；（b）法向壓力為0.50 MPa；（c）法向壓力為0.75 MPa；（d）法向壓力為1.00 MPa

Figure 13. Relationship between JRC and K under different water pressures when normal pressure is constant: (a) normal pressure of 0.25 MPa; (b) normal pressure of 0.50 MPa; (c) normal pressure of 0.75 MPa; (d) normal pressure of 1.00 MPa

下載: 全尺寸圖片幻燈片

圖 14 參數$\delta $與壓力梯度$ - \nabla P$的關系曲線。（a）法向壓力為0.25 MPa；（b）法向壓力為1.00 MPa

Figure 14. Relationship between $\delta $ and $ - \nabla P$: (a) normal pressure of 0.25 MPa; (b) normal pressure of 1.00 MPa

下載: 全尺寸圖片幻燈片

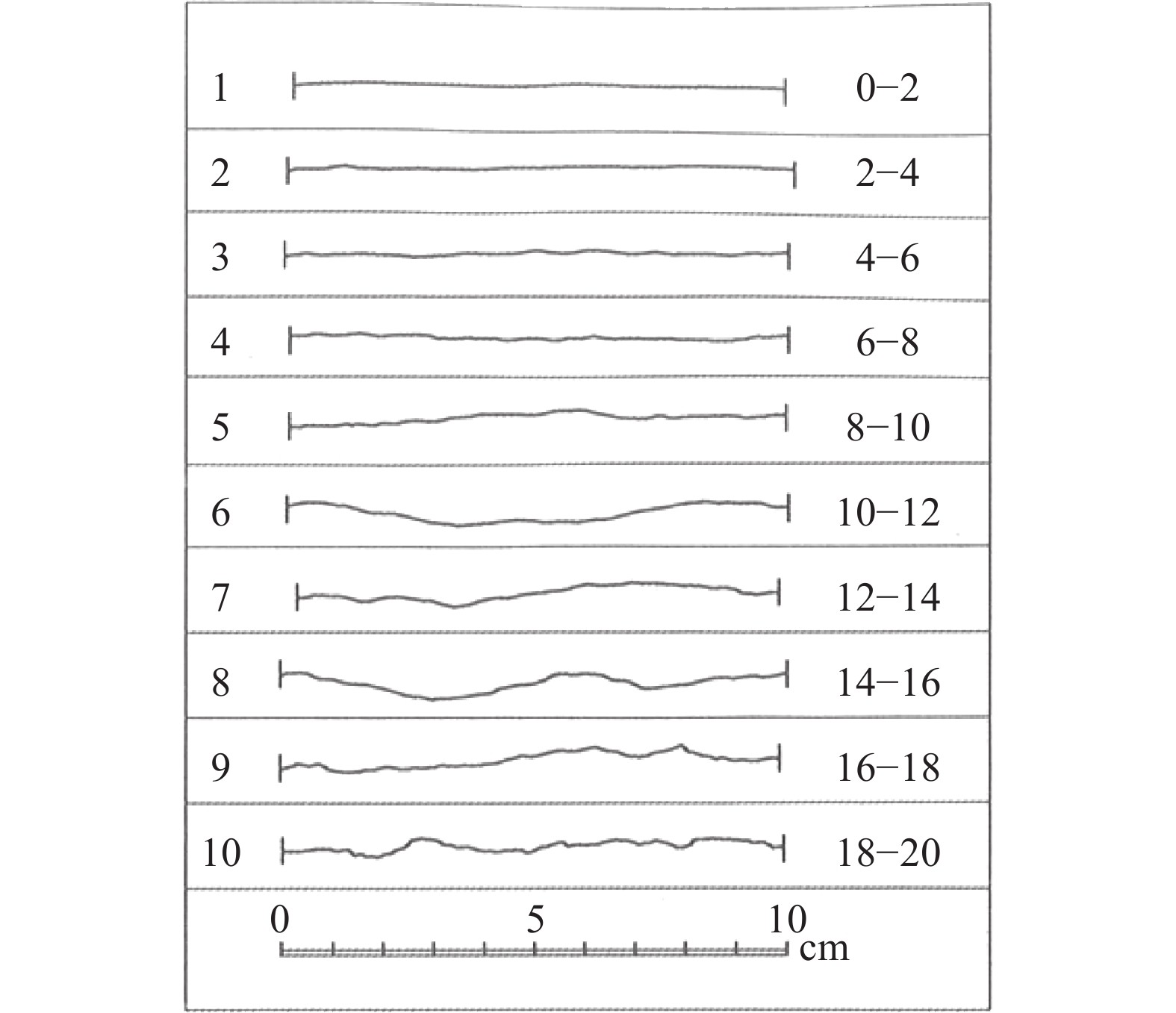
表 1 數字化后JRC的標準曲線圖^[15]

Table 1. Standard curve diagram of JRC after digitization

Number	Standard joint profile	JRC value (Specific value)
1		0–2 (0.4)
2		2–4 (2.8)
3		4–6 (5.8)
4		6–8 (6.7)
5		8–10 (9.5)
6		10–12 (10.8)
7		12–14 (12.8)
8		14–16 (14.5)
9		16–18 (16.7)
10		18–20 (18.7)

下載: 導出CSV

表 2 無法向壓力改變水壓的試驗方案

Table 2. Test scheme for changing hydraulic pressures without normal pressures

Number	Hydraulic pressure, P/MPa	Change value in fracture aperture/mm
1	0.04	0.16
2	0.09	0.17
3	0.14	0.19
4	0.19	0.21
5	0.24	0.23
6	0.29	0.24

下載: 導出CSV

表 3 Forchheimer 方程擬合的數值

Table 3. Values of Forchheimer equation fitting

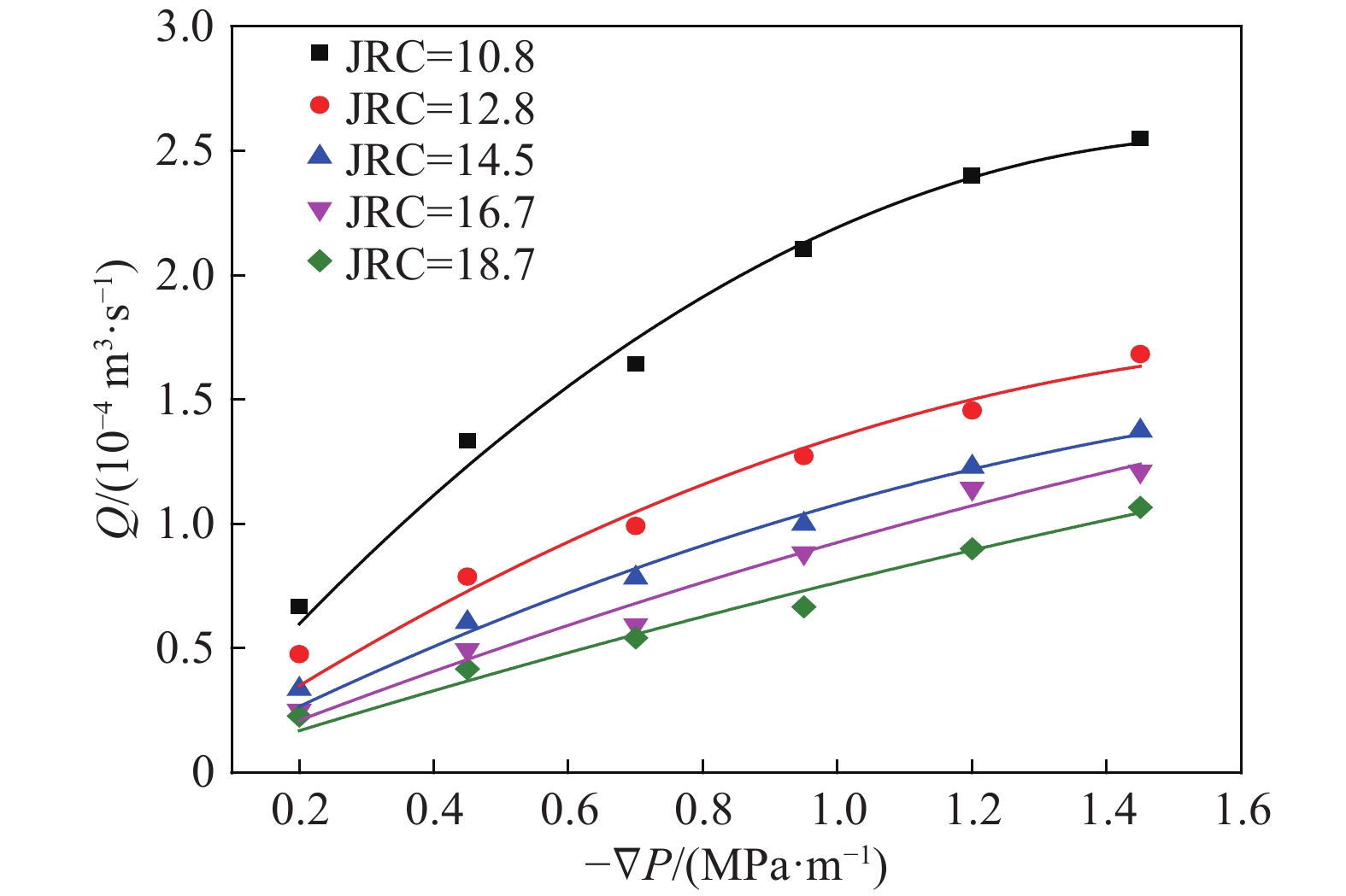
JRC (Specific value)	Coefficient, A	Coefficient, B	Correlation coefficient, R²
6 (10.8)	3.19	?0.99	0.99
7 (12.8)	1.84	?0.49	0.99
8 (14.5)	1.39	?0.31	0.99
9 (16.7)	1.08	?0.15	0.99
10 (18.7)	0.86	?0.09	0.99

下載: 導出CSV

表 4 線性函數擬合的數值

Table 4. Values of linear function fitting

Normal pressure, F/MPa	Hydraulic pressure, P/MPa	Coefficient, a	Coefficient, b	Correlation coefficient, R²	Normal pressure, F/MPa	Hydraulic pressure, P/MPa	Coefficient, a	Coefficient, b	Correlation coefficient, R²
0.25	0.04	26.54	?1.04	0.98	1.00	0.04	12.16	?0.51	0.94
	0.09	28.72	?1.12	0.99		0.09	13.23	?0.51	0.94
	0.14	31.51	?1.23	0.98		0.14	16.18	?0.61	0.97
	0.19	35.21	?1.35	0.97		0.19	17.63	?0.67	0.99
	0.24	45.29	?1.89	0.98		0.24	25.34	?1.05	0.96
	0.29	60.13	?2.65	0.98		0.29	36.60	?1.64	0.98

下載: 導出CSV

表 5 法向壓力恒定不同水力壓力下滲透系數的變化量

Table 5. Permeability change under different hydraulic pressures and constant normal pressure

Normal pressure, F/MPa	Hydraulic pressure, P/MPa	Permeability change, K/(m·s^?1)	Normal pressure, F/MPa	Hydraulic pressure, P/MPa	Permeability change, K/(m·s^?1)
0.25	0.04	8.41	0.75	0.04	3.61
	0.09	8.87		0.09	3.33
	0.14	9.67		0.14	4.53
	0.19	10.37		0.19	6.56
	0.24	15.29		0.24	9.37
	0.29	20.59		0.29	13.88
0.50	0.04	6.37	1.00	0.04	3.75
	0.09	6.72		0.09	4.17
	0.14	7.18		0.14	4.53
	0.19	9.14		0.19	5.12
	0.24	10.66		0.24	8.53
	0.29	16.87		0.29	12.12

下載: 導出CSV

表 6 不同粗糙度裂隙滲流寬度的變化情況

Table 6. Variation of apertures of fractures with different roughnesses

Normal pressure, F/MPa	Hydraulic pressure, P/MPa	Change value in fracture aperture with different JCR, e/mm					Normal pressure, F/MPa	Hydraulic pressure, P/MPa	Change value in fracture aperture with different JCR, e /mm
Normal pressure, F/MPa	Hydraulic pressure, P/MPa	10.8	12.8	14.5	16.7	18.7	Normal pressure, F/MPa	Hydraulic pressure, P/MPa	10.8	12.8	14.5	16.7	18.7
0.25	0.04	0.06	0.05	0.04	0.05	0.04	1.00	0.04	0.03	0.03	0.02	0.02	0.02
	0.09	0.06	0.05	0.05	0.05	0.04		0.09	0.03	0.03	0.02	0.02	0.02
	0.14	0.07	0.06	0.06	0.05	0.04		0.14	0.03	0.04	0.03	0.02	0.02
	0.19	0.07	0.06	0.06	0.05	0.04		0.19	0.04	0.04	0.03	0.03	0.02
	0.24	0.08	0.07	0.0.6	0.06	0.05		0.24	0.04	0.04	0.04	0.03	0.03
	0.29	0.08	0.08	0.07	0.06	0.06		0.29	0.04	0.04	0.04	0.03	0.03

下載: 導出CSV

表 7 負指數函數擬合的數值

Table 7. Values of negative exponential function fitting

Hydraulic pressure, F/MPa	Coefficient, a′	Coefficient, b′	Correlation coefficient, R²
0.04	17.15	?1.72	0.95
0.09	26.88	?1.86	0.91
0.14	65.03	?2.18	0.96
0.19	88.40	?2.29	0.97
0.24	90.23	?2.43	0.96
0.29	102.56	?3.01	0.95

下載: 導出CSV

www.77susu.com

參考文獻(27)

[1]	Rong G, Yang J, Cheng L, et al. Laboratory investigation of nonlinear flow characteristics in rough fractures during shear process. J Hydrol, 2016, 541: 1385 doi: 10.1016/j.jhydrol.2016.08.043
[2]	Wang Z R, Song P, Wen Z Y, et al. Control of fracturing behavior of fractured reservoir under horizontal wells. Chin J Eng, 2020, 42(11): 1449 王志榮, 宋沛, 溫震洋, 等. 裂隙性儲層水平井起裂行為的控制. 工程科學學報, 2020, 42(11):1449
[3]	Ju Y, Dong J B, Gao F, et al. Evaluation of water permeability of rough fractures based on a self-affine fractal model and optimized segmentation algorithm. Adv Water Resources, 2019, 129: 99 doi: 10.1016/j.advwatres.2019.05.007
[4]	Rezaei Niya S M, Selvadurai A P S. Correlation of joint roughness coefficient and permeability of a fracture. Int J Rock Mech Min Sci, 2019, 113: 150 doi: 10.1016/j.ijrmms.2018.12.008
[5]	Zhang X, Chai J R, Qin Y, et al. Experimental study on seepage and stress of single-fracture radiation flow. KSCE J Civil Eng, 2019, 23(3): 1132 doi: 10.1007/s12205-019-1519-7
[6]	Zhu J T, Cheng Y Y. Effective permeability of fractal fracture rocks: Significance of turbulent flow and fractal scaling. Int J Heat Mass Transfer, 2018, 116: 549 doi: 10.1016/j.ijheatmasstransfer.2017.09.026
[7]	Xu G X, Zhang Y X, Ha Q L. Super-cubic and sub-cubic law of rough fracture seepage and its experiments study. J Hydraulic Eng, 2003(3): 74 doi: 10.3321/j.issn:0559-9350.2003.03.014 許光祥, 張永興, 哈秋舲. 粗糙裂隙滲流的超立方和次立方定律及其試驗研究. 水利學報, 2003(3):74 doi: 10.3321/j.issn:0559-9350.2003.03.014
[8]	Su B Y, Zhan M L, Zhao J. Study on fracture seepage in the imitative nature rock. Chin J Geotech Eng, 1995(5): 19 doi: 10.3321/j.issn:1000-4548.1995.05.004 速寶玉, 詹美禮, 趙堅. 仿天然巖體裂隙滲流的實驗研究. 巖土工程學報, 1995(5):19 doi: 10.3321/j.issn:1000-4548.1995.05.004
[9]	Ju Y, Zhang Q G, Yang Y M, et al. An experimental investigation on the mechanism of fluid flow through single rough fracture of rock. Sci Sin Technol, 2013, 43(10): 1144 doi: 10.1360/ze2013-43-10-1144 鞠楊, 張欽剛, 楊永明, 等. 巖體粗糙單裂隙流體滲流機制的實驗研究. 中國科學: 技術科學, 2013, 43(10):1144 doi: 10.1360/ze2013-43-10-1144
[10]	He Y L, Tao Y J, Yang L Z. Experimental research on hydraulic behaviors in a single joint with various values of JRC. Chin J Rock Mech Eng, 2010, 29(Suppl 1): 3235 賀玉龍, 陶玉敬, 楊立中. 不同節理粗糙度系數單裂隙滲流特性試驗研究. 巖石力學與工程學報, 2010, 29(增刊 1):3235
[11]	Duan M B, Li G, Meng Y F, et al. Research on regulation of fracture seepage in different joint roughness coefficients. J Water Resour Water Eng, 2013, 24(5): 41 doi: 10.11705/j.issn.1672-643X.2013.05.009 段慕白, 李皋, 孟英峰, 等. 不同節理粗糙度系數的裂隙滲流規律研究. 水資源與水工程學報, 2013, 24(5):41 doi: 10.11705/j.issn.1672-643X.2013.05.009
[12]	Zhao J W, Lan H D, Yang K, et al. High-resolution fused deposition 3D printing based on electric-field-driven jet. Chin J Eng, 2019, 41(5): 652 趙佳偉, 蘭紅波, 楊昆, 等. 電場驅動熔融噴射沉積高分辨率3D打印. 工程科學學報, 2019, 41(5):652
[13]	Ju Y, Xie H P, Zheng Z M, et al. Visualization of the complex structure and stress field inside rock by means of 3D printing technology. Chin Sci Bull, 2014, 59(32): 3109 doi: 10.1360/csb2014-59-32-3109 鞠楊, 謝和平, 鄭澤民, 等. 基于3D打印技術的巖體復雜結構與應力場的可視化方法. 科學通報, 2014, 59(32):3109 doi: 10.1360/csb2014-59-32-3109
[14]	Wang P T, Liu Y, Zhang L, et al. Preliminary experimental study on uniaxial compressive properties of 3D printed fractured rock models. Chin J Rock Mech Eng, 2018, 37(2): 364 王培濤, 劉雨, 章亮, 等. 基于3D打印技術的裂隙巖體單軸壓縮特性試驗初探. 巖石力學與工程學報, 2018, 37(2):364
[15]	Huang Y B, Zhang Y J, Yu Z W, et al. Experimental investigation of seepage and heat transfer in rough fractures for enhanced geothermal systems. Renewable Energy, 2019, 135: 846 doi: 10.1016/j.renene.2018.12.063
[16]	Zhang Z Y, Nemcik J. Fluid flow regimes and nonlinear flow characteristics in deformable rock fractures. J Hydrol, 2013, 477: 139 doi: 10.1016/j.jhydrol.2012.11.024
[17]	Chen Y D, Lian H J, Liang W G, et al. The influence of fracture geometry variation on non-Darcy flow in fractures under confining stresses. Int J Rock Mech Min Sci, 2019, 113: 59 doi: 10.1016/j.ijrmms.2018.11.017
[18]	Yin Q, He L X, Jing H W, et al. Quantitative estimates of nonlinear flow characteristics of deformable rough-walled rock fractures with various lithologies. Processes, 2018, 6(9): 149 doi: 10.3390/pr6090149
[19]	Zhou J Q, Hu S H, Fang S, et al. Nonlinear flow behavior at low Reynolds numbers through rough-walled fractures subjected to normal compressive loading. Int J Rock Mech Min Sci, 2015, 80: 202 doi: 10.1016/j.ijrmms.2015.09.027
[20]	Barton N, Choubey V. The shear strength of rock joints in theory and practice. Rock Mech, 1977, 10(1-2): 1 doi: 10.1007/BF01261801
[21]	Zhang Q, Li X C, Hu S B, et al. Permeability evolution of coupling granite joint during shearing under high-stress condition. Rock Soil Mech, 2018, 39(10): 3641 張強, 李小春, 胡少斌, 等. 高應力下花崗巖耦合節理在剪切過程中滲透率演化特性. 巖土力學, 2018, 39(10):3641
[22]	Wu Y Q, Zhang Z Y. Introduction to Rock Mass Hydraulics. Chengdu: Southwest Jiaotong University Press, 1994 仵彥卿, 張卓元. 巖體水力學導論. 成都: 西南交通大學出版社, 1994
[23]	Wang Z H, Xu C S, Dowd P. A modified cubic law for single-phase saturated laminar flow in rough rock fractures. Int J Rock Mech Min Sci, 2018, 103: 107 doi: 10.1016/j.ijrmms.2017.12.002
[24]	Pan R J, He X. Seepage law of rough single fracture under the influence of tortuosity of rock fracture surface. J Liaoning Tech Univ Nat Sci Ed, 2020, 39(4): 293 潘汝江, 何翔. 巖石斷裂面曲折度影響下的粗糙單裂隙滲流規律. 遼寧工程技術大學學報(自然科學版), 2020, 39(4):293
[25]	Chen Z, Qian J Z, Luo S H, et al. Experimental study of friction factor for groundwater flow in a single rough fracture. J Hydrodyn Ser B, 2009, 21(6): 820 doi: 10.1016/S1001-6058(08)60218-8
[26]	Rong G, Yang J, Cheng L, et al. A Forchheimer equation-based flow model for fluid flow through rock fracture during shear. Rock Mech Rock Eng, 2018, 51(9): 2777 doi: 10.1007/s00603-018-1497-y
[27]	Yin Q, Ma G W, Jing H W, et al. Hydraulic properties of 3D rough-walled fractures during shearing: An experimental study. J Hydrol, 2017, 555