Stability, convergence, and robustness of deterministic multivariable self-tuning control
-
摘要: 本文用基于傳遞函數概念的虛擬等價系統方法統一分析各種類型的多變量確定性自校正控制系統的穩定性、收斂性和魯棒性,分別針對參數估計收斂到真值、參數估計收斂到非真值以及參數估計不收斂的3種情況給出若干定理、推論和注釋.在各個判據的基礎上,進一步深化對確定性多變量自校正控制系統的理解.所得結論說明:參數估計的收斂性不是確定性多變量自校正控制系統穩定和收斂的必要條件;系統自身的反饋信息對確定性多變量自校正控制是充分的,即外加激勵信號不是必要的.Abstract: Self-tuning control is an important approach to intelligent control system design because this kind of control system uses online parameter estimation (or learning) to derive the model of the plant, and as a result of model parameter estimation (or learning), the controller parameters can be adjusted online. However, we still lack a unified analysis tool (which is independent of specific controller design strategy and parameter estimation algorithm) that can be used by engineers to easily understand and judge the stability, convergence, and robustness of this kind of self-tuning control system. This study is focused on a unified analysis of deterministic multivariable self-tuning control systems with the help of the virtual equivalent system (VES) approach based on the transfer function concept. For different parameter estimation situations (three cases are considered, i.e., parameter estimation converges to its true value, parameter estimation converges to other values, and parameter estimation does not converge), four theorems and two corollaries on the stability, convergence, and robustness of deterministic multivariable self-tuning control systems are given with some remarks. These results are independent of specific controller design strategy and parameter estimation algorithm. From the results obtained in this study, it is concluded that the convergence of parameter estimates is unnecessary for the stability and convergence of a self-tuning control system. The feedback information of the self-tuning control system itself is sufficient to achieve the control objective, i.e., the external excitation signal is unnecessary for the deterministic multivariable self-tuning control system. Moreover, on the basis of the results of the stability, convergence, and robustness of deterministic multivariable self-tuning control systems, we have obtained a profound understanding of the self-tuning control system design method. This understanding will provide more flexibility for engineers in real applications of this kind of controller design strategy.
-
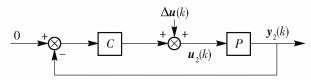
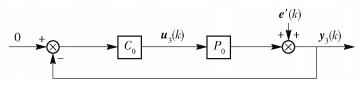
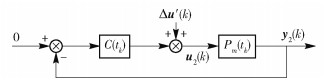
圖 4 參數收斂到真值時的分解子系統2
Figure 4. Decomposed subsystem 2 of Fig. 2
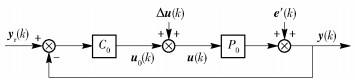
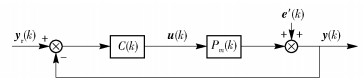
圖 11 參數估計不收斂時的分解子系統1
Figure 11. Decomposed subsystem 1 of Fig. 10
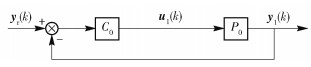
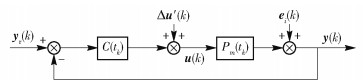
圖 12 參數估計不收斂時的分解子系統2
Figure 12. Decomposed subsystem 2 of Fig. 10
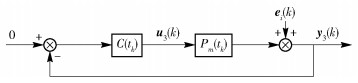
圖 13 參數估計不收斂時的分解子系統3
Figure 13. Decomposed subsystem 3 of Fig. 10
www.77susu.com<span id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> <span id="fpn9h"><noframes id="fpn9h"> <th id="fpn9h"></th> <strike id="fpn9h"><noframes id="fpn9h"><strike id="fpn9h"></strike> <th id="fpn9h"><noframes id="fpn9h"> <span id="fpn9h"><video id="fpn9h"></video></span> <ruby id="fpn9h"></ruby> <strike id="fpn9h"><noframes id="fpn9h"><span id="fpn9h"></span> -
參考文獻
[1] Zhang W C. Research on Robust Adaptive Control Theory and Its Applications [Dissertation]. Beijing: Tsinghua University, 1993張維存. 魯棒自適應控制理論及應用研究[學位論文]. 北京: 清華大學, 1993 [2] Fekri S, Athans M, Pascoal A. Issues, progress and new results in robust adaptive control. Int J Adapt Control Signal Process, 2006, 20(10): 519 doi: 10.1002/acs.912 [3] Li Q Q. Adaptive Control System: Theory, Design, and Applications. Beijing: Science Press, 1990李清泉. 自適應控制系統理論、設計與應用. 北京: 科學出版社, 1990 [4] Xie X M, Ding F. Adaptive Control System. Beijing: Tsinghua University Press, 2002謝新民, 丁鋒. 自適應控制系統. 北京: 清華大學出版社, 2002 [5] Zhang W C. On the stability and convergence of self-tuning control-virtual equivalent system approach. Int J Control, 2010, 83(5): 879 doi: 10.1080/00207170903487421 [6] Goodwin G C, Sin K S. Adaptive Filtering Prediction and Control. Courier Corporation, 2014 http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1164531 [7] Lozano-Leal R, Goodwin G. A globally convergent adaptive pole placement algorithm without a persistency of excitation requirement. IEEE Trans Autom Control, 1985, 30(8): 795 doi: 10.1109/TAC.1985.1104036 [8] Lozano-Leal R. Robust adaptive regulation without persistent excitation. IEEE Trans Autom Control, 1989, 34(12): 1260 doi: 10.1109/9.40771 [9] Lozano R. Singularity-free adaptive pole-placement without resorting to persistency of excitation: detailed analysis for first order systems. Automatica, 1992, 28(1): 27 doi: 10.1016/0005-1098(92)90004-Y [10] Lozano R, Dion J M, Dugard L. Singularity-free adaptive pole placement using periodic controllers. IEEE Trans Autom Control, 1993, 38(1): 104 doi: 10.1109/9.186317 [11] Lozano R, Zhao X H. Adaptive pole placement without excitation probing signals. IEEE Trans Autom Control, 1994, 39(1): 47 doi: 10.1109/9.273338 [12] Xu L Z, Wang X H. Methods and Examples of Mathematical Analysis (Revised Edition). Beijing: Higher Education Press, 1983徐利治, 王興華. 數學分析的方法及例題選講(修訂版). 北京: 高等教育出版社, 1983 [13] Caines P, Lafortune S. Adaptive control with recursive identification for stochastic linear systems. IEEE Trans Autom Control, 1984, 29(4): 312 doi: 10.1109/TAC.1984.1103520 [14] Chen H F, Guo L. Asymptotically optimal adaptive control with consistent parameter estimates. SIAM J Control Optim, 1987, 25(3): 558 doi: 10.1137/0325031 [15] ?str?m K J, Wittenmark B. Adaptive Control. Newyork: Courier Corporation, 2013 [16] Hu S G. Functional Analysis. Beijing: Higher Education Press, 2007胡適耕. 泛函分析. 北京: 高等教育出版社, 2007 [17] Prandini M, Campi M C. A new recursive identification algorithm for singularity free adaptive control. Syst Control Lett, 1998, 34(4): 177 doi: 10.1016/S0167-6911(98)00012-7 [18] Prandini M, Bittanti S, Campi M C. A penalized identification criterion for securing controllability in adaptive control. J Math Syst Estim Control, 1998, 8(4): 1 http://www.ams.org/mathscinet-getitem?mr=1651285 [19] Liberzon D, Morse A S. Basic problems in stability and design of switched systems. IEEE Control Syst Mag, 1999, 19(5): 59 doi: 10.1109/37.793443 [20] Shorten R, Wirth F, Mason O, et al. Stability criteria for switched and hybrid systems. SIAM Rev, 2007, 49(4): 545 doi: 10.1137/05063516X [21] Feng C B, Shi W. Adaptive control. Beijing: Publishing House of Electronics Industry, 1986馮純伯, 史維. 自適應控制, 北京: 電子工業出版社, 1986 [22] Zhang W C, Wei W. Virtual equivalent system theory for adaptive control and simulation verification. Sci Sin Inform, 2018, 48(7): 947 https://www.cnki.com.cn/Article/CJFDTOTAL-PZKX201807014.htm張維存, 魏偉. 自適應控制的虛擬等價系統理論及仿真驗證. 中國科學: 信息科學, 2018, 48(7): 947 https://www.cnki.com.cn/Article/CJFDTOTAL-PZKX201807014.htm -




 下載:
下載: